Physiologische Dynamik bei demyelinisierenden Krankheiten: Enträtseln komplexer Zusammenhänge durch Computermodellierung

Free resource

Title	Physiologische Dynamik bei demyelinisierenden Krankheiten: Enträtseln komplexer Zusammenhänge durch Computermodellierung
Authors	Jay S. Coggan · Stefan Bittner · Klaus M. Stiefel · Sven G. Meuth · Steven A. Prescott
Source	Document
Date	2021
Journal	Int J Mol Sci.
DOI	10.3390/ijms160921215
PUBMED	https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4613250/#!po=53.5714
PDF copy
License	CC BY
This resource has been identified as a Free Scientific Resource, this is why Masticationpedia presents it here as a mean of gratitude toward the Authors, with appreciation for their choice of releasing it open to anyone's access

Physiologische Dynamik bei demyelinisierenden Krankheiten: Enträtseln komplexer Zusammenhänge durch Computermodellierung

Free resource by Jay S. Coggan  · Stefan Bittner · Klaus M. Stiefel  · Sven G. Meuth · Steven A. Prescott

Physiological Dynamics in Demyelinating Diseases: Unraveling Complex Relationships through Computer Modeling

Jay S. Coggan, Stefan Bittner, [...], and Steven A. Prescott

Additional article information

Abstrakt

Trotz intensiver Forschung stehen für die meisten neurologischen Erkrankungen nur wenige Behandlungen zur Verfügung. Demyelinisierende Erkrankungen sind keine Ausnahme. Dies ist vielleicht nicht überraschend angesichts der multifaktoriellen Natur dieser Krankheiten, die komplexe Wechselwirkungen zwischen Zellen des Immunsystems, Glia und Neuronen umfassen. Bei Multipler Sklerose zum Beispiel herrscht unter Forschern Uneinigkeit über die Ursache oder gar welches System oder welcher Zelltyp Ground Zero sein könnte. Diese Situation schließt die Entwicklung und strategische Anwendung mechanismusbasierter Therapien aus. Wir werden diskutieren, wie Computermodellierung, die auf Fragen auf verschiedenen biologischen Ebenen angewendet wird, dabei helfen kann, unterschiedliche Beobachtungen miteinander zu verknüpfen und komplexe Mechanismen zu entschlüsseln, deren Lösungen einem einfachen Reduktionismus nicht zugänglich sind. Indem sie überprüfbare Vorhersagen treffen und kritische Lücken im vorhandenen Wissen aufdecken, können solche Modelle die Forschung unterstützen und einen rigorosen Rahmen bieten, in den neue Daten integriert werden können, sobald sie gesammelt werden. Heutzutage gibt es keinen Mangel an Daten; Die Herausforderung besteht darin, dem Ganzen einen Sinn zu geben. In dieser Hinsicht ist die Computermodellierung ein unschätzbares Werkzeug, das letztendlich unser Verständnis, die Diagnose und Behandlung von demyelinisierenden Krankheiten verändern könnte.

Schlüsselwörter: Myelin, Demyelinisierung, Multiple Sklerose, neurodegenerative Erkrankung, Computermodell, Wirkstoffforschung

Einführung

Die Nervensysteme von Wirbeltieren werden aufgrund ihres Aussehens und der entsprechenden funktionellen Rollen oft in graue und weiße Substanz unterteilt. Während die graue Substanz größtenteils aus Zellkörpern und Dendriten besteht, enthält die weiße Substanz hauptsächlich Axone und hat ihren Namen von den Lipidmembranschichten namens Myelin, die eng um diese Axone gewickelt sind. Myelin stammt aus verschiedenen Klassen von Gliazellen, die als Oligodendrozyten im Zentralnervensystem (ZNS) und Schwann-Zellen im peripheren Nervensystem (PNS) bezeichnet werden.

Die durch die Myelinschichten bereitgestellte elektrische Isolierung verbessert die axonale Funktion, indem sie sowohl die Energieeffizienz als auch die Leitungsgeschwindigkeit von Aktionspotentialen (APs) erhöht. Diese beiden Funktionen haben möglicherweise ihre relative Bedeutung während der Evolution geändert. Myelin tauchte erstmals im Ordovizium (485 bis 443 ma oder Millionen Jahre vor der Gegenwart) auf, nachdem sich die Vorfahren der Neunaugen und Schleimaale von den übrigen Wirbeltierlinien abgespalten hatten.Mit einigen interessanten Ausnahmen, Myelin oder analoge Strukturen kommen in allen Wirbeltieren vor und sind entscheidend für das reibungslose Funktionieren ihres Nervensystems. Der ungefähre Zeitpunkt der Entwicklung von Myelin kann aus der bekannten Zeit der Divergenz zwischen Akkordaten ohne (Agnatha) und mit (alle anderen Wirbeltiere) Myelin abgeleitet werden.

Die Myelinumhüllung wird durch regelmäßig beabstandete, nicht myelinisierte Abschnitte unterbrochen, die als Ranvier-Knoten bekannt sind. Myelin beschleunigt die Leitung, indem es den transmembranen Ladungsfluss durch Ionenkanäle innerhalb der Knoten einschränkt. Innerhalb der sogenannten Internodien fließt Strom das Axon hinunter, wobei nur wenig davon durch die isolierte Zellmembran fließt. Das AP wird an jedem Knoten regeneriert, an dem die Dichte der spannungsgesteuerten Natrium- und Kaliumkanäle sehr hoch ist. Dieser Vorgang wird als „saltatorische Leitung“ bezeichnet, da der AP scheinbar von Knoten zu Knoten springt. Störungen in diesem Schnellfeuer-Kommunikationssystem können mit einer Reihe von Funktionsstörungen des Nervensystems in Verbindung gebracht werden.

Axone scheinen in mehrfacher Hinsicht an physikalischen Grenzen zu operieren. Ein interessantes Beispiel ist, dass die Größe von Axonen durch das thermische Rauschen beschränkt zu sein scheint, das Ionenkanalproteinen innewohnt; Jedes Axon, das dünner als 0,1 μm ist, wäre aufgrund seines hohen Rauschpegels für die Informationsübertragung unbrauchbar. Interessanterweise ist 0,1 μm auch ungefähr der kleinste Axondurchmesser, der in Nervensystemen beobachtet wird [7]. Diese und ähnliche Ergebnisse deuten darauf hin, dass Axone und ihre Unterstrukturen fein abgestimmte biologische Geräte sind, dass die Abstimmung jedoch offensichtlich unter pathologischen Bedingungen gestört werden kann.

Die Demyelinisierung setzt funktionelle Veränderungen in Gang, die für klinische Merkmale wichtig sind, aber nicht ohne weiteres durch immunologische oder radiologische Veränderungen erklärt werden können. Die Lage einer Plaque sagt voraus, welches System betroffen sein wird (motorisch vs. sensorisch, visuell vs. taktil), aber nicht, wie es betroffen sein wird. Dies unterstreicht die Bedeutung der Beurteilung der Funktion (zusätzlich zur Struktur) und wie sie sich nach der Demyelinisierung verändert. Nach der Einführung demyelinisierender Krankheiten werden wir erörtern, wie die klinischen Manifestationen dieser Krankheiten verschiedene pathologische Veränderungen der Axonfunktion widerspiegeln. Wir werden argumentieren, dass das Verständnis dieser Veränderungen und die vollständige Nutzung dieses Verständnisses für diagnostische und therapeutische Zwecke enorm von der Computermodellierung profitieren können.

Demyelinisierende Krankheiten

Abbildung 1: Demyelinisierende Erkrankungen des peripheren Nervensystems (PNS). (A) Primäre demyelinisierende Polyneuropathien und (B) Polyneuropathien mit Axonschädigung. Abkürzungen: CMT 1, 2 und 4: Charcot-Marie-Tooth-Krankheit; CMTX: X-chromosomale Charcot-Marie-Tooth-Erkrankung; HNPP: erbliche Neuropathie mit Neigung zu Drucklähmungen; AIDP: akute entzündliche demyelinisierende Polyneuropathie; GBS: Guillain-Barré-Syndrom. CIDP: chronisch entzündliche demyelinisierende Polyneuropathie; MGUS: monoklonale Gammopathie unbestimmter Bedeutung; POEMS: Polyneuropathie, Organomegalie, Endokrinopathie oder Ödem M-Protein und Hautanomalien; HSAN I–IV: hereditäre sensorische und autonome Neuropathie.

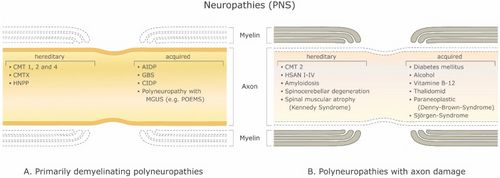
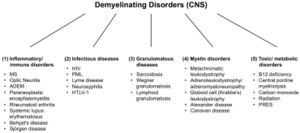
Es gibt eine große Anzahl demyelinisierender Erkrankungen, die sowohl das PNS (Abbildung 1) als auch das ZNS (Abbildung 2) betreffen. Die Ätiologien sind heterogen und reichen von genetischen Störungen bis hin zu metabolischen, infektiösen oder Autoimmunmechanismen. Multiple Sklerose (MS) ist mit schätzungsweise 3 Millionen Patienten weltweit die am weitesten verbreitete dieser Erkrankungen. Die zugrunde liegende Ursache ist ungewiss, es wird jedoch angenommen, dass sie eine genetische Veranlagung für Umwelteinflüsse beinhaltetund kann immunologische, Reaktionsfähigkeit auf Traumata, biophysikalische, genetische und/oder metabolische Komponenten umfassen.Die Symptome und Läsionen müssen zeitlich und räumlich vielfältig sein. Das heißt, es müssen zeitlich mehrere Episoden auftreten, an denen getrennte Teile des zentralen Nervensystems beteiligt sind. Es ist nicht klar, ob die entzündliche Demyelinisierung ein primäres oder sekundäres Ereignis innerhalb des Krankheitsprozesses ist. Die meisten Behandlungen zielen auf das Immunsystem oder die Blut-Hirn-Schranke ab, aber auch die Behandlung neurologischer Symptome durch Modulation der axonalen Erregbarkeit spielt eine wichtige Rolle (siehe unten)..

Abbildung 2: Demyelinisierende Erkrankungen des Zentralnervensystems (ZNS). Abkürzungen: MS: Multiple Sklerose; ADEM: akute disseminierte Enzephalomyelitis; HIV: menschliches Immunschwächevirus; PML: progressive multifokale Leukenzephalopathie; HTLV-1: menschliches T-lymphotropes Virus 1; PRES: posteriores reversibles Enzephalopathie-Syndrom.

Klinische Bewertung von Multipler Sklerose

Die Symptome sind vielfältig und können bei einem einzelnen Patienten in allen Kombinationen auftreten. Die Diagnose erfordert, dass im Laufe der Zeit mehrere Läsionen und symptomatische Episoden vorliegen müssen, an denen nicht verbundene Teile des ZNS beteiligt sind. Darüber hinaus neigen die Symptome dazu, schlecht mit radiologischen Messungen zu korrelieren. In den allermeisten Fällen korrelieren individuelle klinische Merkmale nicht gut mit MRT-Befunden, insbesondere bei zerebralen Läsionen. Diese klinisch-radiologische Dissoziation verlangt nach einem besseren theoretischen Verständnis der Demyelinisierungssymptome und der zugrunde liegenden biophysikalischen Veränderungen, die sie begleiten, was natürlich die Frage aufwirft, was genau mit den betroffenen Axonen passiert.

Die Symptome sind oft intermittierend und können sowohl Funktionsverlust (negative Symptome wie Taubheitsgefühl, Muskelschwäche, Kribbeln, Blindheit, Inkontinenz, Verlust der Sexualfunktion, Gleichgewichtsverlust, undeutliche Sprache, Verstopfung, beeinträchtigende Müdigkeit, Depression, kognitive Dysfunktion) umfassen , Unfähigkeit zu schlucken, Gangstörungen und Verlust der Atemkontrolle) und Funktionsgewinn (unter anderem positive Symptome wie Krämpfe, Spastik, Krämpfe, Schmerzen, verschwommenes oder doppeltes Sehen, Harndrang oder Zögern, Übelkeit)..Frühe differenzialdiagnostische Kriterien sind das Lhermitte-Zeichen (Halsbeugegefühle) und das Uhthoff-Phänomen (temperaturabhängige Verschlechterung der Beschwerden). Die Differenzialdiagnose der MS richtet sich eng nach den McDonald-Kriterien.

In humandiagnostischen Studien zu visuell, sensorisch oder motorisch evozierten Potentialen (VEP, SEP, MEP) kann nur die Latenz oder Leitungsgeschwindigkeit genau gemessen werden (mit etwa 30–40 % Schwankungen zwischen verschiedenen Labors). Aber diese Messungen geben wenig Aufschluss über zugrunde liegende Mechanismen, die eine Verlangsamung oder Blockierung der Leitung beinhalten, oder morphologische oder funktionelle Faktoren wie Verzweigung, Demyelinisierung, Remyelinisierung, axonale Verjüngung (Abnahme der Querschnittsfläche), Dämpfung oder erneutes Wachstum, temperaturbedingte Änderungen der Leitung , oder Malpolarisation (Hyper oder Hypo). Nichtsdestotrotz kann die Art der demyelinisierenden Läsion Hinweise auf die Ätiologie geben und daher die Behandlung leiten; Beispielsweise scheinen genetische Faktoren stärker mit internodalen Krankheitsprozessen zu korrelieren, und immunologische Dysfunktionen verursachen paranodale Anomalien.

Eine Reihe von Tests werden routinemäßig verwendet, um die neurale Funktion zu beurteilen. Bei der Elektroneurographie wird ein kurzer elektrischer Stimulus an einer anatomisch vordefinierten Position an einen peripheren Nerv angelegt, um die Latenz und Amplitude des zusammengesetzten Aktionspotentials an einer anderen Stelle entlang des Nervs zu messen. Die Ergebnisse müssen in Kombination mit klinischen Befunden und Tests (z. B. Elektromyographie) interpretiert werden, aber es ist wichtig, dass verschiedene Krankheiten unterschiedliche Muster elektroneurographischer Veränderungen aufweisen. Dies ist nicht nur für diagnostische Zwecke wichtig, sondern kann auch auf spezifische pathologische Veränderungen der Axonfunktion hinweisen, die wiederum bei der Wahl der Therapie hilfreich sein könnten (wenn die Axonpathobiologie verstanden würde; siehe unten). Unter Verwendung von Threshold-Tracking wurde die Erregbarkeit beim Menschen für verschiedene periphere demyelinisierende Erkrankungen gemessen, darunter die Charcot-Marie-Tooth-Krankheit Typ 1A (CMT1A), die chronisch entzündliche demyelinisierende Polyneuropathie (CIDP), das Guillain-Barré-Syndrom (GBS) und die multifokale motorische Neuropathie (MMN). ).Die Herausforderung liegt in der Interpretation dieser Beobachtungen. Zu diesem Zweck hat die Gruppe von Stephanova zunehmend größere Grade systematischer und fokaler Demyelinisierung von Motorfasern simuliert, um zu versuchen, die beobachteten physiologischen Veränderungen zu erklären (siehe Abschnitt „Modellierung“ weiter unten).

Beteiligung von Zellkörpern

Die Progression von schubförmig remittierender MS (RRMS) zur sekundär progredienten MS (SPMS) ist mit einer stärkeren Beteiligung der Pathologie der grauen Substanz verbunden, obwohl eine Beteiligung der Axone/der grauen Substanz bereits in frühen Krankheitsstadien beobachtet werden kann. Die Schädigung der grauen Substanz gilt als zugrunde liegender Mechanismus des Krankheitsverlaufs und der dauerhaften Behinderung bei MS-Patienten und wird durch den Verlust der Hirnparenchymfraktion oder des Gehirnvolumens durch MRT oder klinisch durch Progression auf der erweiterten Behinderungsstatusskala (EDSS) gemessen.Der Übergang von RRMS zu SPMS ist ein Vorzeichen für den Mangel an Therapeutika zur Bekämpfung der verschlimmerten körperlichen und kognitiven Verschlechterung, mit der die meisten SPMS-Patienten konfrontiert sind.

Behandlung

Die wichtigsten Eingriffe bei MS umfassen die Modulation der Immunantwort mit beispielsweise Methly-Prednisolon, Interferon betas, Glatirameracetat oder Fingolimod oder die Verhinderung der Überquerung der BHS durch Entzündungszellen (monoklonale Antikörper, z. B. Tysabri (Anti-α4-Integrin, Natalizumab )). Vor kurzem wurden die ersten beiden oralen Wirkstoffe (Fumarat und Teriflunomid) sowie der gegen CD52 gerichtete Antikörper Natalizumab für die Behandlung von RRMS zugelassen, die erfolgreich mit Erstlinientherapien wie Interferonen, Glatirameracetat oder Fingolimod oder durch behandelt werden kann Zweitlinientherapien, aber progressive Formen (PPMS, SPMS) stellen immer noch einen ungedeckten biomedizinischen Bedarf dar. Antineoplastika werden in extrem fortgeschrittenen oder schwierigen Fällen eingesetzt.

Krankheitsmodifizierende Medikamente sind entscheidend, um den Demyelinisierungsprozess zu stoppen oder zumindest abzuschwächen, aber ebenso wichtig ist es, die Symptome zu behandeln, die sich aus einer bereits aufgetretenen Demyelinisierung ergeben. Die Ionenkanalmodulation wird mit dem Aufkommen neuer Ionenkanalblocker wie Ampyra (K-Kanal-Blockade) zunehmend vielversprechend. Die Kaliumkanalblockade soll die Erregbarkeit von Axonen verbessern. Das Problem ist, dass solche Eingriffe, obwohl sie bei der Behandlung negativer Symptome und der Wiederherstellung der Funktion wirksam sind, dazu neigen, positive Symptome zu verschlimmern. Umgekehrt kann die Behandlung positiver Symptome wie Spasmen mit Antiepileptika wie beispielsweise Carbamazepin negative Symptome verstärken. Tatsächlich reduziert das Blockieren von Na+-Kanälen nicht nur positive Symptome, es kann auch neuroprotektiv sein (weil die Ansammlung von Na+ dazu führt, dass Na+/Ca2+-Austauschmechanismen Neuronen mit Ca2+ beladen, das exzitotoxisch ist). (Abbildung 3), aber diese Vorteile gehen zu Lasten negativer Symptome. Daher und insbesondere bei einem Patienten, der eine Mischung aus positiven und negativen Symptomen aufweist, sind die Behandlungsmöglichkeiten eingeschränkt.

Mechanismen der demyelinisierungsbedingten Neurodegeneration. Demyelinisierung kann fortschreitend zu ionischen Ungleichgewichten, Energiekrise, Leitungsblock und schließlich Neurodegeneration führen. (A) ein normaler Knoten von Ranvier mit intakten juxtaparanodalen, paranodalen und nodalen Regionen, die darstellen $Na^{+},K^{+},Ca^{+}$Ionen fließen durch ihre jeweiligen Kanäle mit Mitochondrien, die das ATP für energieabhängige liefern $Na^{+},K^{+}ATP$asen, die die Ionengradienten wiederherstellen, die durch den Ionenfluss durch die Kanäle erschöpft sind. Im Axon sind zahlreiche verschiedene Ionenkanäle vorhanden, aber hier ist nur eine kleine Teilmenge dargestellt; (B) partielle Demyelinisierung führt zur Auflösung von Knotenionenkanälen, Energiemangel und Ungleichgewichten von Ionengradienten; (C) Eine vollständige Demyelinisierung kann zu einem Leitungsblock und einer axonalen Degeneration aufgrund der Akkumulation von intrazellulärem führen $Ca^{+}$ die aus Energiekrisen und Störungen des Ionengleichgewichts resultieren. Abkürzungen: $K_{v}1$: Kaliumkanal Typ 1; $Na_{v}1.6$ und $Na_{v}1.2$: Natriumkanaltypen 1.6 und 1.2;; $Na^{+},Ca^{+}$Tauscher:$Na^{+},Ca^{+}$ Austauschpumpe; $Na^{+},K^{+}ATP$ase: ATP (Energie)-abhängig $Na^{+},K^{+}$Austauschpumpe; CASPR1: Contactin-assoziiertes Protein 1 (Wechselwirkungsmolekül zwischen myelinisierender Zelle und Axon);$NF55$: Neurofascin 155 (vorherrschendes Wechselwirkungsmolekül zwischen Myelin und Axon an der paranodalen Axo-Glia-Verbindung).

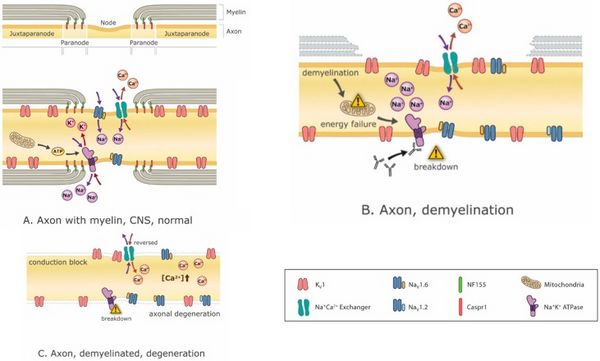
Die obige Diskussion wirft den wichtigen Punkt auf, dass, obwohl viel Lärm um Immunmechanismen gemacht wurde, ihre Verbindung mit klinischen Veränderungen weitgehend korreliert ist. Man muss die intermediären Wirkungen auf die axonale Funktion berücksichtigen, nämlich die primären und sekundären (kompensatorischen) Änderungen der Axon-Erregbarkeit, um zu verstehen, wie die neurologische Funktion verändert wird. Diese Veränderungen sind keine einfachen und direkten Folgen der Demyelinisierung, sondern legen stattdessen nahe, dass sich die axonale Physiologie selbst als Reaktion auf die Demyelinisierung verändert. Einige dieser Veränderungen sind adaptiv, während andere maladaptiv sind, oder vielleicht können adaptive Veränderungen maladaptiv werden, wenn sich die Situation (Myelinisierungsstatus) weiterentwickelt. Wenn Veränderungen in der Axonphysiologie die Manifestation verschiedener Symptome diktieren, dann wird die Symptombehandlung weitgehend auf Behandlungen fallen, die darauf abzielen, die Axonphysiologie zu manipulieren. Die strategische Entwicklung solcher Behandlungen erfordert ein tiefes, mechanistisches Verständnis der axonalen Erregbarkeit und ihrer Regulation.

Axonpathobiologie

Strukturelle und molekulare Veränderungen

Axone sind stark von Demyelinisierung betroffen. Die Axonmorphologie wird unregelmäßig oder geschwollen, oft mit einem perligen Aussehen. Eine fokale Akkumulation von Proteinen (durch schnellen axonalen Transport) wird ebenfalls beobachtet. Bei chronisch aktiven Plaques ist ein axonaler Verlust von 20–80 % in der weißen Substanz der Periplaque und in der normalen entfernten weißen Substanz erkennbar. Bei früh aktiven und chronisch aktiven Plaques wird angenommen, dass die Schädigung durch Entzündungs- und Immunfaktoren verursacht wird, die während der akuten entzündlichen Demyelinisierung freigesetzt werden. Vorgeschlagene Mediatoren umfassen Proteasen, Cytokine, Excitotoxine und freie Radikale. Neuronale Antigene sind Ziele einer Immunreaktion, die zu einer ZNS-Entzündung führt. Andere Faktoren, die eine axonale Dysfunktion oder den Tod verursachen, umfassen einen Mangel an trophischer Unterstützung durch Myelin und Oligodendrozyten, Schäden durch lösliche oder zelluläre Immunfaktoren, die noch in der inaktiven Plaque vorhanden sind, und chronisches Mitochondrienversagen bei erhöhtem Energiebedarf. Eine entscheidende Rolle für Oligodendrozyten und Schwann-Zellen beim Überleben von Axonen wurde auch den Peroxisomen, dem Lipidstoffwechsel und der Entgiftung reaktiver Sauerstoffspezies (ROS) zugeschrieben.

Remyelinisierung wird häufig als Schattenplaques beobachtet, die durch die Rekrutierung von undifferenzierten Oligodendrozyten-Vorläufern gebildet werden, die zu den Läsionen wandern und diese umgeben, wodurch dünne Schichten der Remyelinisierung ermöglicht werden. Dieser Prozess tritt meist in akuten aktiven Plaques auf, aber auch in chronischen Phasen. Diese Beobachtung löste die Entwicklung eines neuen monoklonalen Antikörpers aus, der gegen LINGO-1 gerichtet ist (Anti-LINGO-1). Die Bindung von LINGO-1 an Nogo-Rezeptoren verhindert remyelinisierende Prozesse im ZNS; die Hemmung dieser Wechselwirkung ermöglicht somit eine signifikante Remyelinisierung bei Tieren mit experimenteller autoimmuner Enzephalomyelitis.

Während des Krankheitsprozesses können autoreaktive Lymphozyten und Makrophagen die Blut-Hirn-Schranke überwinden und sich im Gehirn und Rückenmark ansammeln. Regulatorische Lymphozyten (Tregs) unterdrücken Effektorzellen nicht – meist zytotoxische CD8+-Zellen. Die Freisetzung von entzündungsfördernden Zytokinen rekrutiert naive Mikroglia, die durch Wechselwirkungen mit Fc- und Komplementrezeptoren Kontakt mit einer Oligodendrozyten-Myelin-Einheit aufnehmen. Ein zytotoxisches, den Tod auslösendes Signal wird dann durch den oberflächengebundenen Tumornekrosefaktor α (TNFα) übertragen.. Dies tritt zusammen mit ausgedehnten axonalen Schäden auf.

Lucchinetti el al.schlugen vier unterschiedliche Immunmuster der Plaquebildung vor, die bei Patienten in verschiedenen Stadien der Krankheit gefunden wurden. Plaques vom Typ I und II werden von T-Lymphozyten- und Makrophagen-Entzündungen dominiert und es wird angenommen, dass sie T-Zell- bzw. T-Zell-plus-Antikörper-Autoimmun-Enzephalomyelitis-Modelle nachahmen. Myelinverlust in Typ-I-Plaques kann durch toxische Faktoren verursacht werden, die von aktivierten Makrophagen freigesetzt werden, während IgG- und Komplementablagerung auf eine Rolle von Antikörpern in Typ-II-Plaques hindeuten. Im Gegensatz dazu zeigen die Muster III und IV eine große Oligodendrozyten-Dystrophie. Es wird angenommen, dass Muster III mit Hypoxie-induzierten Läsionen zusammenhängt, die durch Defekte in der mitochondrialen Funktion verursacht werden, wohingegen Muster-IV-Läsionen mit tiefgreifendem nicht-apoptotischem Tod von Oligodendrozyten in der weißen Substanz der Periplaque assoziiert sind.

Barnett and Prineas analysierten Läsionen von Patienten direkt nach dem Einsetzen eines Rezidivs, während dessen eine aktive Plaquebildung andauerte. Ihre Ergebnisse legen nahe, dass Oligodendrozyten-Apoptose und Glia-Aktivierung während der frühen aktiven Plaquebildung in Abwesenheit von entzündlichen Lymphozyten oder Myelin-Phagozyten auftreten. Sie schlugen vor, dass die Anfälligkeit von Oligodendrozyten, die in Lucchinettis Typ-III-Muster beschrieben wird, in den frühen Stadien aller Plaquebildung vorhanden ist und der Auslöser für die nachfolgende postapoptotische Nekrose ist, die in späteren Stadien die Phagozytose von Myelin durch Makrophagen einleitet. In-vitro-Analysen dieses Prozesses haben Komplementkaskaden, Tumornekrosefaktoren oder gasförmige Second Messenger impliziert.Obwohl die Identifizierung von Plaques und die Überwachung ihres Fortschritts einen wichtigen klinischen Wert haben, gibt es nur eine bescheidene Korrelation zwischen der Belastung durch demyelinisierende Läsionen, wie sie durch herkömmliches MRI bestimmt wird, und der klinischen Behinderung von Patienten mit MS (siehe oben).

Funktionale Änderungen

Zu den Mechanismen der funktionellen Beeinträchtigung während der Demyelinisierung gehören häufig die Störung der transmembranen Na+-, K+- und Ca2+-Ionen, die Ausbreitung ihrer entsprechenden Ionenkanäle, eine Abnahme der Effizienz der AP-Leitung und eine daraus resultierende Stoffwechselkrise (Abbildung 3). Eine Demyelinisierung kann leicht einen Leitungsausfall innerhalb des betroffenen Axons erklären. Wenn die Leitung nicht vollständig ausfällt, kann die Leitungsgeschwindigkeit dennoch verlangsamt werden, und eine unterschiedliche Verlangsamung über verschiedene Axone kann variable Leitungsverzögerungen verursachen, die zu einem desynchronisierten Spiking führen.

Die Demyelinisierung ermöglicht auch, dass entblößte Axone eng aneinander liegen, wodurch die Voraussetzungen für ephaptische Wechselwirkungen und Übersprechen geschaffen werden. Eine Reflexion kann auch aufgrund einer Impedanzfehlanpassung zwischen myelinisierten und nicht myelinisierten Axonlängen auftreten. Andererseits kann Übererregbarkeit nicht direkt der Demyelinisierung zugeschrieben werden; Stattdessen müssen sekundäre Veränderungen der intrinsischen Erregbarkeit herangezogen werden, um Phänomene wie die Erzeugung ektopischer Spitzen und Nachentladung (AD) zu erklären. Veränderungen der Erregbarkeit stellen wahrscheinlich kompensatorische Veränderungen dar, die darauf abzielen, die Funktion nach der direkt durch Demyelinisierung verursachten Störung wiederherzustellen, was mit einem Prozess übereinstimmt, der als homöostatische Plastizität bezeichnet wird, aber diese Kompensation kann offensichtlich maladaptiv sein. Jedes der oben genannten Ergebnisse, die sich nicht gegenseitig ausschließen, trägt dazu bei, unterschiedliche Symptome hervorzurufen, die bei demyelinisierenden Erkrankungen beobachtet werden.

Paroxysmale Symptome, die durch das plötzliche Einsetzen oder Verstärken von Symptomen wie Spasmen oder stechenden Schmerzen gekennzeichnet sind, entstehen wahrscheinlich durch AD oder anderweitig unangemessenes Spiking vom Burst-Typ. Solche Spiking-Muster legen hochgradig nichtlineare Wechselwirkungen zwischen dem beitragenden Ionenstrom nahes and could, in theory at least, involve interactions between different regions of the neuron. Im Gegensatz zu allgemeineren Formen der Übererregbarkeit (z. B. erhöhte Feuerrate oder reduzierte Schwelle) sind diese spezifischen Muster in Bezug auf die genauen Mechanismen, durch die sie entstehen können, begrenzt. Daher kann die Identifizierung der Ionenkanalveränderungen, die diesen spezifischen Formen der Übererregbarkeit zugrunde liegen, dazu beitragen, die Suche nach Ionenkanalveränderungen einzuschränken, die für assoziierte, jedoch weniger ausgeprägte Formen der Übererregbarkeit verantwortlich sind.

Die Störung des Energiegleichgewichts in einem Neuron könnte sich auch tiefgreifend auf das Wohlbefinden des Neurons auswirken (Abbildung 3). Tatsächlich können kompensierende Änderungen gewisse Funktionen wiederherstellen, aber ohne das Hauptproblem umzukehren, können andere Probleme auftreten. Selbst wenn zum Beispiel ein Leitungsblock durch eine geeignete kompensierende Änderung der Erregbarkeit verhindert wird (d. h. eine, die nicht zu einer Übererregbarkeit führt), kann das System weniger energieeffizient sein. Der Verlust der Energieeinsparungen durch Saltatorische Leitung induziert eine kompensatorische mitochondriale Energieproduktion, die zu oxidativen Schäden und Neurodegeneration führen kann.

Es ist keine leichte Aufgabe, diese lange Liste neurobiologischer Veränderungen im Auge zu behalten, die Wechselbeziehungen zwischen diesen Veränderungen zu verstehen und diese Veränderungen letztendlich mit klinischen Manifestationen zu verknüpfen und eine wirksame Behandlung anzuwenden. Zu diesem Zweck ist die computergestützte Modellierung ein unschätzbares Werkzeug. Simulationen dienen nicht nur dazu, bereits bekannte Informationen zu organisieren, sondern identifizieren auch entscheidende Wissenslücken. Die vernünftige Verwendung von Computermodellen kann daher ein umfassenderes Verständnis ermöglichen und die effektivere Anwendung dieses Verständnisses erleichtern, wie unten erörtert.

Computermodellierung

Insbesondere in Verbindung mit traditionellen Experimenten ist die Computermodellierung unverzichtbar, um inkonsistente Daten und komplexe Mechanismen zu verstehen. Diese Vorteile werden durch die Anwendung von Simulationen in anderen Bereichen, wie z. B. Epilepsie, veranschaulicht. Hier geben wir einen Überblick über die Geschichte der computergestützten Modellierung von Axonen, Ionenleitfähigkeiten, der Physiologie von Myelin und Demyelinisierung, des Immunsystems, der Mitochondrien und anderer biologischer Faktoren, die für das Verständnis demyelinisierender Krankheiten entscheidend sind. Unsere Übersicht erhebt keinen Anspruch auf Vollständigkeit, bietet jedoch eine breite Einführung in vergangene, gegenwärtige und zukünftige Bemühungen auf diesem Gebiet.

Modellierung von Axonen

Die computergestützte Modellierung von Axonen hat sich taxonomisch weiterentwickelt, von Tintenfisch- zu Säugetiergeweben mit einer entsprechenden Zunahme an Raffinesse. Das Modell von Hodgkin und Huxley (HH), das die erste gründliche Erklärung der AP-Erzeugung lieferte, wurde aus Experimenten an nicht myelinisierten Riesenaxonen von Tintenfischen abgeleitet, aber dieses frühe Modell hat sich als unschätzbares Werkzeug erwiesen, aus dem sich später anspruchsvollere Modelle myelinisierter Axone entwickelt haben.

Die räumliche und biophysikalische Heterogenität, die durch die Zugabe von Myelin verliehen wird, und die daraus resultierende Bildung von Knoten und internodalen Regionen, repräsentiert eine signifikante Erhöhung der Axonkomplexität. Das erste Computermodell eines myelinisierten Axons war ein eindimensionales Modell, das die Myelinscheide in das darunter liegende passive Axolemm kollabierte, eine einheitliche räumliche Schrittweite verwendete, um die diskrete Näherung zu bilden, die in der numerischen Lösung verwendet wurde, und eine HH-Charakterisierung der Knotenmembran verwendete. Goldman & Albus modifizierten dieses Modell, um eine Beschreibung der Knotenmembran aufzunehmen, die aus experimentellen Daten von myelinisierten Xenopus laevis-Nervenfasern abgeleitet wurde, wie von Frankenhaeuser & Huxley bestimmt. Nachfolgende Studien haben die gleiche Grundform für das Modell mit einigen Variationen für die Darstellung des Axolemma verwendet. Das Einzelkabelmodell, das das Axon und alle seine Leitfähigkeits- und Kapazitätseigenschaften in einer Kabelgleichung beschreibt, hat das Feld bis heute dominiert, trotz der Einführung von Doppelkabelmodellen durch Blight. In Doppelkabelmodellen werden das internodale Axolemm und die Myelinscheide unabhängig voneinander dargestellt. Das Doppelseilmodell wurde von Halter und Clark erweitertum die Auswirkungen der komplexen Geometrie von ZNS-Oligodendrozyten (oder Schwann-Zellen im Fall des PNS) zu untersuchen.

Neuere Modelle haben auch frühere Vereinfachungen verbessert, darunter die anatomische Komplexität des Ranvier-Knotens, die Verteilung von Ionenkanälen im Axon unter der Myelinscheide, die unterschiedlichen elektrischen Eigenschaften der Myelinscheide und des Axolemmas und die Anpassung an einen möglichen Stromfluss darin der Periaxonalraum. Anatomische Darstellungen des paranodalen Bereichs haben eine detailliertere Beurteilung der Auswirkungen einer traumatischen Hirnverletzung (TBI) auf myelinisierte Axone ermöglicht.Eines der anatomisch ausgefeiltesten Modelle umfasst die Darstellung der komplexen wässrigen Hüllenstruktur von Myelinlamellen als eine Reihe von miteinander verbundenen parallelen Lamellen in einem Modell motorischer Nerven.

Neuere Modelle haben auch die ungleichmäßige Verteilung von Ionenkanälen im gesamten Axon berücksichtigt [19,84,85,86,87,88,89,90].Neben Ionenkanälen bieten energieabhängige Pumpen und andere Ionentransportmechanismen wichtige therapeutische Ziele für eine Reihe von neurologischen Störungen. In dieser Hinsicht kostet die Regulierung der Transmembran-Ionengradienten erhebliche Energie und wird selbst zu einer wichtigen Überlegung (siehe unten).. Dies gilt insbesondere, da das kleine Volumen von Axonen sie anfällig für Ionenkonzentrationsänderungen macht, die sich dramatisch auf die Antriebskräfte auswirken können und in Modellen problematisch werden können, die konstante intrazelluläre und extrazelluläre Konzentrationen annehmen. Aber neuere Modelle haben sich auch mit solchen Problemen befasst (siehe unten).

Alle oben genannten Modelle konzentrieren sich auf die Simulation der Änderung des Axonmembranpotentials, aber man hat nicht unbedingt experimentellen Zugang zu dieser Variablen, was natürlich die Bemühungen erschwert, Simulations- und experimentelle Daten zu vergleichen. Da extrazelluläre Aufzeichnungen die primäre Quelle elektrophysiologischer Daten von menschlichen Probanden sind, ist die mathematische Beschreibung des extrazellulären Feldpotentials klinisch von großem Interesse. Zur Berechnung dieser Potentiale werden mathematische Auswertungen auf der Grundlage von Laplace-Gleichungen und Fourier-Transformationen verwendet (manchmal auch als Line-Source-Modellierung bezeichnet, z.,.

Modellierung spezifischer Mechanismen

Über die Modellierung der normalen axonalen Funktion hinaus können Modelle verwendet werden, um bestimmte Mechanismen der axonalen Dysfunktion zu untersuchen, insbesondere wenn sie mit experimentellen Ergebnissen kombiniert werden, die die Mechanismen besser lokalisieren könnten.Zum Beispiel, Barrett and Barrett zeigten, dass das depolarisierende Nachpotential (DAP) empfindlich auf Änderungen der Leitfähigkeitsdichten und kapazitiven Änderungen reagiert, die während der Demyelinisierung auftreten können. Ein Modell von Blight wurde zur Simulation seiner experimentellen Aufnahmebedingungen entworfenund stellt ein einzelnes Internodium mit mehreren diskreten Segmenten und benachbarten Knoten und Internodien in einzelnen Segmenten mit konzentrierten Parametern dar. Dieses Modell umfasste K+-Kanäle im Axolemma des einzelnen multisegmentierten Internodiums und behandelt den Rest als rein passiv.

Aufbauend auf dieser Arbeit, mit sorgfältiger Beachtung anatomischer und elektrophysiologischer Details,McIntyre et al. befassten sich mit der Rolle des DAP und der Nachhyperpolarisation (AHP) im Erholungszyklus – dem ausgeprägten Muster der Schwellenfluktuation nach einem einzelnen Aktionspotential, das von menschlichen Nerven gezeigt wird. Die Simulationen legten unterschiedliche Rollen für aktive und passive Na+- und K+-Kanäle in beiden Nachpotentialen nahe und schlugen vor, dass Unterschiede in der AP-Form, Stärke-Dauer-Beziehung und dem Erholungszyklus von motorischen und sensorischen Nervenfasern kinetischen Unterschieden in den Knoten-Na+-Leitfähigkeiten zugeschrieben werden können . Richardsonet al. fanden auch heraus, dass eine Änderung des Standardmodells des „perfekten Isolators“ notwendig ist, um DAPs während der Hochfrequenzstimulation zu reproduzieren.

Die Temperaturempfindlichkeit von Demyelinisierungseffekten wurde ebenfalls rechnerisch untersucht. Zlochiver modellierten eine anhaltende Resonanzreflexion über eine einzelne fokale Demyelinisierungsplaque und stellten fest, dass dieser Effekt empfindlich auf Temperatur und Axondurchmesser reagierte. Alle diese Beispiele demonstrierten die Leistungsfähigkeit von Simulationen, um spezifische Mechanismen zu untersuchen, um beobachtete Phänomene aus der Klinik zu erklären und eine Anleitung für zukünftige Forschung zu bieten.

Wie oben erwähnt, manifestieren deutliche Veränderungen in der Axonfunktion wahrscheinlich bestimmte Funktionsgewinn- oder -verlustsymptome. Wenn man diese Änderungen in einem Rechenmodell reproduzieren könnte, könnten die notwendigen Parameteränderungen, die zum Umwandeln des Modells zwischen normalem und abnormalem Betrieb erforderlich sind, verwendet werden, um die zugrunde liegende Pathologie vorherzusagen. Im Idealfall kann dies zu konkreten Experimenten führen, in denen beispielsweise der verdächtige Ionenkanal direkt manipuliert wird, um zu sehen, ob seine akute Veränderung ausreicht, um bestimmte pathologische Veränderungen zu reproduzieren oder rückgängig zu machen. Jüngste Studien aus dem Prescott-Labor veranschaulichen diesen Prozess. Dieser Erfolg dieser Studien hing von fortschrittlichen Techniken ab, einschließlich der dynamischen Klemmtechnik, die verwendet wird, um zwischen normalen und abnormalen Spiking-Mustern und optogenetischen Werkzeugen zu wechseln. Der nächste Schritt besteht darin, Veränderungen in der Axonfunktion mit Krankheitssymptomen (oder ihren Verhaltenskorrelaten in Tiermodellen) zu verknüpfen.

In Hörnervenexperimenten Tagoe und Kollegen zeigten, dass Hörverlust im Zusammenhang mit morphologischen Veränderungen an Paranoden und Juxtaparanoden, einschließlich der Verlängerung des Hörnervs um Ranvier-Knoten, aus der Exposition gegenüber lautem Lärm resultieren kann. Hamann und Kollegen erweiterten diese Arbeit und bauten ein Computermodell, um mögliche Mechanismen zu untersuchen. Ihr Modell legte nahe, dass es wahrscheinlicher ist, dass eine Abnahme der Dichte von Na-Kanälen als eine Umverteilung von Na- oder K-Kanälen im Allgemeinen für die mit akustischer Überexposition verbundene Leitungshemmung verantwortlich ist. Dieses Experiment-Modell-Tandem demonstriert das aufschlussreiche Potenzial der Paarung von Computermodellen mit Laborexperimenten.

Mit einem mehrschichtigen Modell mit myelinisiertem Axon konnten Stephanova und Kollegen fortlaufend erfolgreich wahrscheinliche anatomische und physiologische Mängel identifizieren, die verschiedenen Symptomen und Zuständen im Zusammenhang mit der Demyelinisierung zugrunde liegen, indem sie Vergleiche mit den Schwellenverfolgungsmessungen von Patienten anstellten, einschließlich Latenzen, Refraktärität (die Erhöhung der Schwelle Strom während der relativen Refraktärzeit), Refraktärzeit, Supernormalität und Schwellenelektrotonuswerte, einschließlich Stimulus-Reaktions-Maßnahmen wie Strom-Schwellen-Beziehungen.Beispielsweise fanden sie heraus, dass eine leichte internodale systematische Demyelinisierung (ISD) ein spezifischer Indikator für CMT1A ist. Milde paranodale systematische Demyelinisierung (PSD) und paranodale systematische Demyelinisierung (PISD) sind spezifische Indikatoren für CIPD und ihre Subtypen. Schwere fokale Demyelinisierungen, internodal und paranodal, paranodal-internodal (IFD und PFD, PIFD) sind spezifische Indikatoren für erworbene demyelinisierende Neuropathien wie GBS und MMN [18] (siehe Abbildung 1).

Leichte systematische und schwere fokale Demyelinisierung entsprechen erblichen (CMT1A) und erworbenen (CIDP, GBS und MMN) Neuropathien (Tabelle 1). Es wurde auch festgestellt, dass 70 % der systematischen Demyelinisierung nicht ausreichen, um Symptome zu verursachen, und dass 96 % für einen Leitungsblock an einem einzelnen Knoten erforderlich sind [18]. Somit besteht ein großer Sicherheitsfaktor für die fokale Demyelinisierung. Mit ihrer temperaturabhängigen Version des Modells der myelinisierten menschlichen motorischen Nervenfaser, Stephanova und Daskalova zeigten, dass die elektrotonischen Potentiale bei Patienten mit CIDP während Hypo- und sogar leichter Hyperthermie einem hohen Blockierungsrisiko ausgesetzt sind, und deuten auf Mechanismen hin, die eine erhöhte Größe der polarisierenden elektrotonischen Knoten- und depolarisierenden internodalen elektrotonischen Potentiale, einen Anstieg der nach innen gerichteten Gleichrichter-K+- und Leck-K+-Ströme mit der Temperatur umfassen, und die Akkommodation bei lang anhaltender Hyperpolarisation ist größer als bei Depolarisation.

Table 1 Correspondence between types of demyelination and diseases according to Stephanova and Dimitrov.
Type of Demyelination	Corresponding Disease (PNS)
Internodal systematic demyelination (ISD)	Charcot-Marie-Tooth Disease Type 1A (CMT1A)
Paranodal systematic demyelination (PSD)	Chronic inflammatory demyelinating polyneuropathy (CIDP)
Paranodal + internodal demyelination (PISD)	Chronic inflammatory demyelinating polyneuropathy (CIPD) subtypes
Internodal focal demyelination (IFD)	Guillain-Barré (GBS)
Paranodal focal demyelination (PFD)	Multifocal Motor Neuropathy (MMN)
Paranodal + focal demyelination (PIFD)	Multifocal Motor Neuropathy (MMN)

Simple Models and Nonlinear Dynamical Analysis

Given the temporal dissociation between the manifestation of symptoms and the rates of demyelination and remyelination, homeostatic processes undoubtedly occur within axons, which include the redistribution of ion channels in demyelinated plaques. But given the diversity of ion channels expressed by different axons and only patchy knowledge of how expression levels change, building detailed models to investigate those homeostatic processes is problematic. Especially under those conditions, highly simplified models can help identify fundamental principles, as exemplified by joint use of modified HH and Morris-Lecar models [57,58]. The results of those studies suggested a simple explanation for the breadth of symptoms encountered during demyelination by revealing that the ratio of Na+ to leak K+ conductance, g(Na)/g(L), acted as a four-way switch controlling excitability patterns that included failure of AP propagation, normal AP propagation, AD, and spontaneous spiking.

Further studies with this model suggested the potential for competition or cooperation between different regions of the same neuron. Cooperativity between remote sites of ectopic spiking allows AD to be initiated and maintained at different locations within a single axon, thus providing a compelling explanation for the temporal and spatial discontinuities of pain and other symptoms presented by MS patients. Remarkably, in a recent study of demyelinated axons in a cuprizone mouse model, experimental evidence was seen for a redistribution of ion channels from the node of Ranvier, enhanced ectopic excitability along with antidromically propagated APs from the demyelinated plaque, as well as a compensatory shift in the excitability of membranes proximal to the soma. All of these observations concur or are consistent with the computational model predictions of Coggan and colleagues and imply the success of the computational approach to guiding laboratory studies.

Furthermore, these simplified models enabled application of mathematical tools to examine the nonlinear mechanisms by which AD is initiated and terminated. Bifurcation analysis revealed the underlying bistability of axon excitability under pathological conditions, as well as the factors controlling the transition from one attractor state to another. AD, for example, requires a slow inward current that allows for two stable attractor states, one corresponding to quiescence and the other to repetitive spiking (a limit cycle). Termination of AD was explained by the attractor associated with repetitive spiking being destroyed. This occurred when ultra-slow negative feedback in the form of intracellular Na+ accumulation caused the destruction of the limit-cycle attractor state [58]. Other studies using bifurcation analysis suggest that ion concentration changes can introduce slow dynamics that may be important for understanding pathological outcomes [94,109].

Modeling at Small Scales

Studies mentioned above highlight the importance of ion concentration changes but each of them only considered those changes at a relatively course scale. By comparison, the study by Lorpreore et al. tackled the daunting problem of modeling three-dimensional electro-diffusion of ion fluxes in micro and nano-domains surrounding ion channels at the node of Ranvier. In this unique model, the fluxes of ions are calculated by Poisson-Nernst-Planck equations with finite volume techniques. The fluxes and electric potentials were evaluated within voxels formed by a Delaunay-Voronoi mesh of the axon interior and exterior close to the membrane. Importantly, the algorithm was validated and results agreed with cable model predictions. Divergence from cable model predictions at smaller cluster sizes revealed the importance of each channel’s own electric field.

The above example highlights the point that models can simulate more than ion channels and membrane potential. Indeed, models can and must dig deeper into biophysical mechanisms like electro-diffusion and into signaling pathways that ultimately serve to regulate ion channel function and expression. A promising method called Biochemical Systems Theory (BST) may be useful in the future for pre-screening the effects of drugs at the systemic level. Broome and Coleman demonstrated the power of this technique by modeling several biochemical pathways in neurons associated with cell death during MS including reactive oxygen and nitrogen species formation, Ca2+ dynamics, death complex formation, apoptotic factor release, and inflammatory responses together with three different states: normal, MS disease and treatment. At the atomic-level, a computational model of myelin basic protein (MBP) structure was carried-out because post-translational modifications of MBP may contribute to demyelination in MS. It is important to understand its 3D structure to predict interaction sites with other molecules but a crystal structure for this protein might never be measured directly. This type of modeling may, therefore, represent an effective way to predict the structure by combining knowledge of amino acid sequence with information from similar proteins. The challenge for and the true power of modeling lies in connecting mechanisms that operate at vastly different scales, from molecular structure to the nervous system as a whole, and beyond, to address how the nervous system interacts with the immune system.

Models of Immune Factors. While there are numerous computational models of the immune system, those related to MS typically model genetic interaction networks, either represented as sets of ordinary differential equations (ODEs) or Boolean networks. One systems biology model of a possible cellular mechanism of RRMS found breakdown in homeostasis of effector (Teff) and regulatory T (Treg) cells. By changing parameters in the Teff-Treg feedback loop, under continual stochastic external stimulus from antigens, the model reproduced spontaneous and apparently stochastic immune relapses. The irreversible damage from each episode accumulates over time. Novel predictions include the suggestion that the timing of Treg immunotherapy in the immune response cycle is critical in determining whether intervention is beneficial or deleterious.

Models of Mitochondrial Dysfunction. As mentioned above, myelin enables more energy efficient AP conduction along the axon. The increased energy demands placed on the demyelinated axon represents yet another challenge to the afflicted neuron. Beyond the loss of saltatory conduction, there is mounting evidence of a critical role for astrocytes and oligodendrocytes in supplying energy to neurons and this process has also been the subject of computational modeling.

There are many ways mitochondrial function can go awry and the compensatory pathways are equally complicated. For example, mitochondrial dysfunction can be rooted in perturbed Ca2+ signaling within mitochondria, disrupted proton gradients or electron chain, reduction-oxidation imbalance as well as the consequences of reduced ATP availability, locally and globally. Multi-scale models of heart, for example, have been used to link altered mitochrondrial Ca2+ signaling to arrhythmia [60]. Using mitochondrial network modeling, this study demonstrated how even slightly too much reactive oxygen species can trigger a cell-wide collapse of mitochondrial membrane potential. This is an excellent example of how a computational model can link processes occurring at different levels, and it is precisely these linkages that must be established in the field of demyelination diseases.

Missing Links and the Need for Integration

Within the field of demyelinating diseases, modeling efforts have traditionally focused on axon models aimed at explaining various aspects of excitability. But as outlined above, those models have undergone tremendous evolution in complexity. In the process, models at different biological scales have begun to coalesce. For instance, models have now begun to address the regulation of ion concentrations and the consequences thereof for slow excitability changes, energy consumption, and toxicity. A computational approach will be necessary for integrating parallel and multifactorial etiologies associated with cognitive decline such as immune system signaling, energy metabolism, grey and white matter interactions, and genetic networks [117]. These continued efforts are starting to uncover the vast and interconnected feedback loops that operate across a broad range of spatial and temporal scales. That said, such efforts are still in their infancy and wide gaps remain in the modeling of demyelinating diseases. It is easier to describe what has been modeled than what has not. A truly integrated model involving multiple cell types that addresses all the hypothesized etiological factors remains unrealized. Among the unexplored or under-explored but potentially useful targets for modeling are grey matter pathology, myelin sheath aqueous layers, energy metabolism, and perhaps most importantly, multi-scale or integrated modeling. One should recognize that the necessary tools exist in other fields of study and can, therefore, be readily applied to the study of demyelination diseases.

Conclusions

The normal physiological function of the CNS or PNS relies on a highly regulated interplay of neurons, glia, vasculature and immune cells. This process encompasses and integrates numerous cellular and signaling components that produce a dynamical, computational whole. When any part goes awry, the entire system is forced to compensate. Even when compensation manages to rescue the most obvious consequences of demyelination, certain processes may not return to a completely normal state, which can lead to problems on longer time scales. The resulting symptoms are a confusing mixture of direct and compensatory changes that continuously evolve. The overall complexity has proven to be intractable to efficient experimental dissection. The application of computational modeling techniques represents an invaluable approach to help break the impasse and engender a new era of understanding and discovery.

Acknowledgments

Support provided by the Canadian Institutes of Health Research New Investigator Award and the Ontario Early Researcher Award (SAP). We thank Heiki Blum for assistance with figure preparation.

Author Contributions

All authors contributed to the writing of this manuscript. Figures were provided by Sven G. Meuth.

Conflicts of Interest

The authors declare no conflict of interest.

Article information

Int J Mol Sci. 2015 Sep; 16(9): 21215–21236. Published online 2015 Sep 7. doi: 10.3390/ijms160921215 PMCID: PMC4613250 PMID: 26370960 Jay S. Coggan,1,* Stefan Bittner,2 Klaus M. Stiefel,1 Sven G. Meuth,2 and Steven A. Prescott3,4 Christoph Kleinschnitz, Academic Editor 1NeuroLinx Research Institute, La Jolla, CA 92039, USA; E-Mail: gro.xniloruen@sualk 2Department of Neurology, Institute of Physiology, Universitätsklinikum Münster, 48149 Münster, Germany; E-Mails: moc.kooltuo@renttib-nafets (S.B.); ed.retsneumku@htuem.nevs (S.G.M.) 3Neurosciences and Mental Health, the Hospital for Sick Children, Toronto, ON M5G 1X8, Canada; E-Mail: ac.sdikkcis@ttocserp.evets 4Department of Physiology and the Institute of Biomaterials and Biomedical Engineering, University of Toronto, Toronto, ON M5G 1X8, Canada

• Author to whom correspondence should be addressed; E-Mail: gro.xniloruen@yaj; Tel.: +1-858-243-6720.

Received 2015 May 26; Accepted 2015 Aug 25. Copyright © 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/). Articles from International Journal of Molecular Sciences are provided here courtesy of Multidisciplinary Digital Publishing Institute (MDPI)