|
|
| (11 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| Condividi
| | == Introduzione == |
|
| |
|
| | Nel capitolo precedente, '[[Transverse Hinge Axis]]', abbiamo introdotto la cinematica mandibolare concentrandoci sul piano sagittale. Durante i movimenti di protrusione e retrusione, la mandibola non si muove esclusivamente lungo l'asse <math>X</math>, ma ruota attorno al centro dell'asse <math>Y</math>. Questo movimento condilare si manifesta anteriormente, dove l'incisivo mandibolare segue traiettorie curvilinee inverse, risultato di un complesso moto spaziale generato dalla rototraslazione sugli assi condilari. Lo spazio angolare risultante, noto come 'Spazio libero Interincisivo', è essenziale per consentire movimenti masticatori fluidi e senza ostacoli. |
|
| |
|
| Hai detto:
| | Questo 'Spazio libero Interincisivo' riveste un ruolo cruciale nelle funzioni masticatorie. Tuttavia, strumenti come il Sirognatograph e i sistemi elettromagnetici tradizionali trascurano la componente rotazionale dei movimenti condilari, focalizzandosi principalmente sulle traslazioni. Sebbene ciò possa essere sufficiente per alcune registrazioni, tale approccio è limitato nel cogliere la complessità dei movimenti mandibolari a sei gradi di libertà. |
| Dovresti cercare di capire il senso di tutto il contentuo che abbiamo elaborato in questo questo capitolo e fare una conclusione corposa di almento 1000 parole per chiudere in bellezza l'argomento. Carico il wikitesto: Punto C_L(7) calcolato: (183.43000, -380.71000)
| |
| Verifica distanza da M7: 34.19000 ==Descrizione della Calibrazione: da Pixel a Millimetri==
| |
|
| |
|
| La calibrazione di un'immagine per ottenere misurazioni accurate richiede l'attenzione a diversi fattori critici. Estrarre distanze da un'immagine può essere complesso, poiché la precisione dipende da:
| | '''Cinematica Mandibolare a Sei Gradi di Libertà''' |
|
| |
|
| #Fattori di distorsione: Le immagini possono essere affette da distorsioni ottiche, che devono essere corrette calibrando la camera utilizzando, ad esempio, una scacchiera di riferimento.
| | Il movimento mandibolare avviene in uno spazio tridimensionale e può essere descritto come un complesso moto spaziale. Ogni condilo è associato a tre assi principali: |
| #Effetto prospettico: La scala di riferimento varia con la distanza dal piano di acquisizione. Per oggetti posti a diverse profondità, è necessario applicare fattori di scala specifici, calcolati utilizzando un modello come quello della pin-hole camera.
| |
| #Distorsioni prospettiche: Queste possono essere corrette utilizzando ottiche telecentriche, particolarmente utili per applicazioni che richiedono un'elevata accuratezza, come nelle misurazioni spaziali o bioingegneristiche.
| |
|
| |
|
| Con questa premessa, il fattore di scala utilizzato nel nostro studio rappresenta un'approssimazione valida nel contesto specifico delle immagini 2D acquisite in condizioni controllate. Tuttavia, per applicazioni più rigorose, come quelle descritte sopra, è necessario considerare strumenti e metodi avanzati per la calibrazione.
| | * Asse <math>Y</math> (latero-mediale): Definisce la rotazione attorno all'asse cerniera trasversale (<math>_tHA</math>, transverse Hinge Axis). |
| | * **Asse <math>Z</math> (verticale):** Definisce la rotazione sull'asse cerniera verticale (<math>_vHA</math>). |
| | * **Asse <math>X</math> (antero-posteriore): Definisce la rotazione attorno all'asse cerniera orizzontale (<math>_oHA</math>). |
|
| |
|
| ==Procedura di Calibrazione e Analisi==
| | A ciascun asse corrisponde un piano di riferimento anatomico: |
|
| |
|
| Per l'analisi dei movimenti mandibolari, è stato utilizzato un modello grafico derivato da uno studio di bioingegneria meccanica, in cui i movimenti dei condili e degli incisivi sono stati registrati. Per garantire l'accuratezza delle misurazioni, l'immagine è stata calibrata convertendo i valori da pixel a millimetri utilizzando una scala di riferimento presente nell'immagine. La conversione avviene con il seguente fattore di conversione:
| | * '''Piano sagittale:''' Mostra il tracciato condilare prodotto dal movimento di rototraslazione dell'asse trasversale (<math>_tHA</math>). |
| | * '''Piano coronale:''' Associato all'asse orizzontale (<math>_oHA</math>). |
| | * '''Piano assiale:''' Legato al movimento generato attorno all'asse verticale (<math>_vHA</math>, noto anche come asse cerniera verticale). |
|
| |
|
| <math>\text{Fattore di conversione} = \frac{\text{Distanza reale (mm)}}{\text{Distanza misurata (pixel)}} = \frac{10 \, \text{mm}}{99.3 \, \text{pixel}} \approx 0.1007 \, \text{mm/pixel}.</math>
| | Va evidenziato che un piano non è generato da un asse; un asse può al massimo essere contenuto in un piano o rappresentare una direzione. Più precisamente, il movimento di un asse genera una 'superficie rigata', che descrive le traiettorie spaziali risultanti. |
|
| |
|
| ===Precisione delle Coordinate dei Punti===
| | '''Asse cerniera verticale''' |
|
| |
|
| Le coordinate dei punti misurati nell'immagine sono espresse in valori continui (con decimali), derivanti da algoritmi di interpolazione sub-pixel che aumentano la precisione della localizzazione. Tuttavia, queste coordinate non corrispondono ai pixel discreti della griglia originale dell'immagine, ma a una stima interpolata della posizione reale del punto nel piano 2D. Le misurazioni fanno riferimento alla proiezione dei punti nello spazio tridimensionale sul piano 2D specifico (ad esempio, il piano <math>(X, Y)</math>).
| | Ci concentreremo sull’asse cerniera verticale (<math>_vHA</math>) per la sua rilevanza nei sistemi di registrazione cinematici come pantografi, elegnatografi e assiografi. Tuttavia, è necessario esaminare il razionale della '''Gnatologia Classica''' per comprendere l'interazione tra piani e assi nel descrivere i movimenti condilari. |
|
| |
|
| ===Misurazione della Distanza tra i Punti===
| | * Il pantografo analogico è stato considerato un dispositivo capace di riprodurre con precisione i movimenti di confine dei tracciati condilari e di trasferirli su un articolatore completamente regolabile tramite le sue 6 piastrine.<ref>Curtis, D.A. ∙ Sorensen, J.A. Errors incurred in programming a fully adjustable articulator with a pantograph ''J Prosthet Dent.'' 1986; 55:427-429</ref><ref>Clayton, J.A. ∙ Kotowicz, W.E. ∙ Zahler, J.M. Pantographic tracings of mandibular movements and occlusion ''J Prosthet Dent.'' 1971; 75:389-395</ref><ref>Shields, J.M. ∙ Clayton, J.A. ∙ Sindledecker, L.D. Using pantographic tracings to detect TMJ and muscle dysfunctions ''J Prosthet Dent.'' 1978; 39:80-87</ref> |
|
| |
|
| Per ogni coppia di punti nell'immagine, la distanza è calcolata utilizzando la formula della distanza euclidea nel piano <math>(X, Y)</math>. Ad esempio, la distanza tra il punto <math>1L</math> e <math>2L</math> (coordinate: <math>1L = (63.1721, -59.6914)</math> e <math>2L = (62.9, -76.6) </math>) è calcolata come segue:
| | * Successivamente, si è riportato che anche il pantografo elettronico registrava i determinanti condilari con un intervallo accettabile (argomento trattato nei capitoli successivi).<ref>Payne, J. Condylar determinants in a patient population: electronic pantograph assessment ''J Oral Rehabil.'' 1997; 24:157-163</ref> |
|
| |
|
| ====Calcolo della Distanza====
| | * Un determinante particolare del movimento condilare, la traslazione laterale immediata mandibolare (Movimento di Bennett), è stato oggetto di dibattito e confusione nella letteratura protesica.<ref>Bennett, N.G. A contribution to the study of the movements of the mandible ''Proc R Soc Med.'' 1908; 1:79-98</ref> Tuttavia, una recente revisione della letteratura ha evidenziato una mancanza di prove sul significato clinico di questo movimento.<ref>Taylor, T.D. ∙ Bidra, A.S. ∙ Nazarova, E. ... Clinical significance of immediate mandibular lateral translation: A systematic review ''J Prosthet Dent.'' 2016; 115:412-418</ref> |
| | <blockquote>'''Nota sulla Precisione e Sugli Obiettivi dello Studio''' |
|
| |
|
| La formula della distanza euclidea è:
| | Questo studio mira a fornire una comprensione concettuale dei principi cinematici coinvolti nella dinamica masticatoria, con un focus sulla biomeccanica mandibolare. Sebbene i calcoli siano stati eseguiti con rigore, potrebbero verificarsi discrepanze dovute a: |
| <math>d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.</math>
| |
|
| |
|
| *'''Differenze lungo gli assi:''' | | * ''Approssimazioni nei dati numerici'': Differenze nei valori cartesiani legate a variabili operative. |
| <math>x_2 - x_1 = 62.9 - 63.1721 = -0.2721,</math>
| | * ''Limiti di rappresentazione'': Uso di numeri approssimati per motivi pratici. |
| <math>y_2 - y_1 = -76.6 - (-59.6914) = -76.6 + 59.6914 = -16.9086.</math>
| | * ''Finalità cliniche'': Lo scopo è descrivere concetti piuttosto che ottenere precisione assoluta. |
| | </blockquote> |
|
| |
|
| *'''Quadrati delle differenze:'''
| | [[File:Figura_1_finale_mod..jpg|center|thumb|600x600px|'''Figura 1:''' <small>Cinematica mandibolare sul piano assiale rappresentata dai markers prelevati dallo strumento ogni 20 mSec. Questi punti rappresentano i condili laterotrusivi dal punto <math>L_c </math> e mediotrusivi <math>M_c </math>. |
| <math>(x_2 - x_1)^2 = (-0.2721)^2 \approx 0.0740,</math> | |
| <math>(y_2 - y_1)^2 = (-16.9086)^2 \approx 285.75.</math> | |
|
| |
|
| *'''Somma dei quadrati:'''
| | Il ''Laterotrusive point'' (a sinistra) e il ''Mediotrusive point'' (a destra) tracciano la posizione dei condili della mandibola durante un movimento masticatorio laterale, che include movimenti complessi di traslazione e rotazione. I punti numerati (<math>1L_c </math>....<math>8L_c </math>) seguono il movimento del condilo laterotrusivo nel tempo, mentre i punti <math>1M_c </math>....<math>8M_c </math> seguono il condilo mediotrusivo. Nell'area del ''Molar point'' e dell' ''Incisal point'' sono rappresentati i percorsi occlusali durante la masticazione.</small>]] |
| <math>(x_2 - x_1)^2 + (y_2 - y_1)^2 = 0.0740 + 285.75 = 285.824.</math> | |
|
| |
|
| *'''Radice quadrata:'''
| | '''Passi Successivi''' |
| <math>d = \sqrt{285.824} \approx 16.91 \text{pixel} </math>
| |
|
| |
|
| *'''Conversione in millimetri:'''
| | In questo capitolo, analizzeremo la cinematica dell'asse verticale (<math>_vHA</math>) e il fenomeno masticatorio, rappresentandolo con tracciati estratti da lavori di riferimento come quello di Lund e Gibbs.<ref> |
| <math>d = 16.91 \, \text{pixel} \cdot 0.1007 \, \text{mm/pixel} \approx 1.70 \, \text{mm}.</math> | | N A Wickwire, C H Gibbs, A P Jacobson, H C Lundeen. [https://pubmed.ncbi.nlm.nih.gov/6971588/ Chewing patterns in normal children]. Angle Orthod. 1981 Jan;51(1):48-60.</ref>(Figura 1) |
|
| |
|
| | == Descrizione della Calibrazione: da Pixel a Millimetri == |
|
| |
|
| ===Nota sulle Coordinate e sulle Convenzioni===
| | La calibrazione di un'immagine per ottenere misurazioni accurate richiede l'attenzione a diversi fattori critici. Estrarre distanze da un'immagine può essere complesso, poiché la precisione dipende da: |
|
| |
|
| Le coordinate sono riferite alla proiezione nel piano <math>(X, Y)</math>, e i valori decimali rappresentano la posizione stimata mediante interpolazione. Nei calcoli effettuati, è stato adottato il sistema di riferimento standard utilizzato in geometria, in cui: | | # ''Fattori di distorsione'': Le immagini possono essere affette da distorsioni ottiche, che devono essere corrette calibrando la camera utilizzando, ad esempio, una scacchiera di riferimento. |
| *l'asse <math>X</math> rappresenta il movimento **antero-posteriore**,
| | # ''Effetto prospettico'': La scala di riferimento varia con la distanza dal piano di acquisizione. Per oggetti posti a diverse profondità, è necessario applicare fattori di scala specifici, calcolati utilizzando un modello come quello della pin-hole camera. |
| *l'asse <math>Y</math> rappresenta il movimento **latero-mediale**.
| | # ''Distorsioni prospettiche'': Queste possono essere corrette utilizzando ottiche telecentriche, particolarmente utili per applicazioni che richiedono un'elevata accuratezza, come nelle misurazioni spaziali o bioingegneristiche. |
|
| |
|
| Tuttavia, software come GeoGebra possono adottare convenzioni opposte, con: | | Con questa premessa, il fattore di scala utilizzato nel nostro studio rappresenta un'approssimazione valida nel contesto specifico delle immagini 2D acquisite in condizioni controllate. Tuttavia, per applicazioni più rigorose, come quelle descritte sopra, è necessario considerare strumenti e metodi avanzati per la calibrazione. |
| *<math>X</math> per il movimento **latero-mediale**,
| |
| *<math>Y</math> per il movimento **antero-posteriore**.
| |
|
| |
|
| Questa discrepanza non incide sul risultato delle distanze calcolate, poiché la formula della distanza euclidea è indipendente dall'orientamento degli assi. Le coordinate sono state riorganizzate solo per adattarsi alla convenzione predefinita del software.
| | '''Calcolo della Distanza tra i Punti''' |
|
| |
|
| | Le coordinate dei punti sono: |
|
| |
|
| ==Cinematica dei Condili==
| | <math>Q_2(525.3, -406)</math> e <math>R_2(764.4, -407.1)</math> |
| '''Traslazioni e Rotazioni dei Condili'''{{Tooltip|2='''Spiegazione del Movimento''': In sintesi, i condili si muovono nello spazio in modo tridimensionale complesso, combinando spostamenti lineari con rotazioni attorno agli assi cartesiani. La rappresentazione delle loro posizioni nel tempo tramite vettori permette di descrivere accuratamente le traiettorie durante il movimento masticatorio.'''Esempio di Movimento''' *Il '''condilo laterotrusivo''' non si limita a traslare lateralmente, ma ruota anche attorno agli assi <math>x</math>, <math>y</math> e <math>z</math>, influenzando la traiettoria dei punti dentali (come incisivo e molare) durante i movimenti mandibolari. Il 'condilo mediotrusivo' si sposta principalmente lungo l'asse mediale con una rotazione secondaria, necessaria per bilanciare il movimento della mandibola.'''Conclusione''' Questa rappresentazione vettoriale consente di calcolare con precisione le '''posizioni, velocità e accelerazioni''' dei condili in un modello tridimensionale, fondamentale per comprendere le dinamiche mandibolari durante il ciclo masticatorio.}}
| |
|
| |
|
| Nel contesto del movimento mandibolare, i condili non eseguono solo movimenti traslatori (spostamenti lineari nello spazio), ma anche rotatori (movimenti angolari attorno a specifici assi). Questo doppio movimento, noto come '''rototraslazione''', è essenziale per comprendere la complessità della cinematica mandibolare.
| | La formula per la distanza euclidea è: |
|
| |
|
| | <math>d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}</math> |
|
| |
|
| Per descrivere in modo accurato la posizione e il movimento di ciascun condilo nel tempo, possiamo utilizzare un insieme di vettori di posizione. Questi vettori, che rappresentano i punti nel sistema di riferimento cartesiano, variano in modulo e direzione a seguito del moto elicoidale. Il moto può essere descritto combinando spostamenti lineari e variazioni angolari, che influenzano la posizione dei vettori stessi all'interno dello spazio tridimensionale.
| | Sostituendo i valori: |
|
| |
|
| Vettori di Posizione del Condilo Laterotrusivo (Lavorante)
| | <math>d = \sqrt{(764.4 - 525.3)^2 + (-407.1 - (-406))^2}</math> |
|
| |
|
| Il condilo laterotrusivo si trova sul lato in cui avviene la laterotrusione, ovvero lo spostamento laterale della mandibola. Durante il movimento, la posizione del condilo può essere descritta mediante un vettore di posizione, definito come il segmento orientato che congiunge il condilo a un’origine del sistema di riferimento cartesiano scelto.Il vettore di posizione varia nel tempo sia in modulo che in direzione, a causa della natura complessa del moto elicoidale. Questo permette di rappresentare il movimento del condilo come una combinazione di spostamenti lineari e cambiamenti di orientamento nel sistema tridimensionale.
| | <math>d = \sqrt{(239.1)^2 + (-1.1)^2}</math> |
|
| |
|
| | <math>d = \sqrt{57121.81 + 1.21} = \sqrt{57123.02} \approx 239.02 \, \text{pixel}</math> |
|
| |
|
| | '''Conversione della Scala in mm''' |
| | |
|
| |
|
| Il '''vettore di posizione''' del condilo laterotrusivo nel tempo è descritto da:
| | Dato che il segmento di <math>239.02 \, \text{pixel}</math> equivale a <math>1 \, \text{cm} = 10 \, \text{mm}</math>, calcoliamo la conversione in mm/pixel: |
|
| |
|
| <math> | | <math>\text{Scala in mm/pixel} = \frac{\text{Lunghezza reale (in mm)}}{\text{Distanza in pixel}} = \frac{10}{239.02} \approx 0.04184 \, \text{mm/pixel}</math> |
| P_l(t) = [X_l(t), Y_l(t), Z_l(t), \theta_l(t), \phi_l(t), \psi_l(t)]
| | |
| </math> | | Quindi, ogni pixel nella figura corrisponde a circa: |
| | |
| | <math>0.04184 \, \text{mm/pixel}</math>. |
| | |
| | '''Esempio di Applicazione: Conversione Distanza in mm''' |
| | |
| | Supponiamo di voler calcolare una distanza in mm. Ad esempio, se la distanza in pixel fosse <math>d = 100 \, \text{pixel}</math>: |
| | |
| | <math>d_\text{mm} = 100 \cdot 0.04184 \approx 4.184 \, \text{mm} </math> |
|
| |
|
| Dove:
| | '''Risultato Finale''' |
|
| |
|
| *<math>X_l(t), Y_l(t), Z_l(t)</math>: Rappresentano gli '''spostamenti lineari''' del condilo laterotrusivo lungo i tre assi dello spazio cartesiano:
| | La scala è: |
| **<math>X_l(t)</math>: Spostamento lungo l'asse antero-posteriore (avanti e indietro). | | * <math>239.02 \, \text{pixel/cm}</math> |
| **<math>Y_l(t)</math>: Spostamento lungo l'asse latero-mediale (destra e sinistra).
| | * <math>0.04184 \, \text{mm/pixel}</math> |
| **<math>Z_l(t)</math>: Spostamento lungo l'asse verticale (alto e basso)
| |
| **<math>\theta_l(t)</math>, <math>\phi_l(t)</math>, <math>\psi_l(t)</math>: Sono le rotazioni angolari del condilo laterotrusivo attorno ai tre assi del sistema di riferimento cartesiano scelto. Queste rotazioni rappresentano il cambiamento di orientamento del condilo nello spazio, descritto utilizzando la convenzione degli angoli di Eulero. È fondamentale notare che le rotazioni non sono commutative, e quindi l'ordine in cui avvengono le rotazioni deve essere specificato per garantire una descrizione univoca.
| |
|
| |
|
| Nel nostro caso, adottiamo la convenzione <math>X,Y,Z</math> che descrive le rotazioni nel seguente ordine:
| | Questi valori possono essere usati per convertire qualsiasi distanza misurata in pixel nella figura in unità metriche come millimetri o centimetri. |
|
| |
|
| *<math>\theta_l(t)</math>: Rotazione attorno all'asse <math>x</math> (causa una torsione laterale della mandibola).
| | == Cinematica dei Condili == |
|
| |
|
| *<math>\phi_l(t)</math>: Rotazione attorno all'asse <math>y</math> (controlla l'apertura e la chiusura della mandibola).
| | '''Traslazioni e Rotazioni dei Condili''' |
|
| |
|
| *<math>\psi_l(t)</math>: Rotazione attorno all'asse <math>z</math> (controlla la rotazione laterale/mediale della mandibola).
| | Nel contesto del movimento mandibolare, i condili eseguono sia movimenti traslatori (spostamenti lineari) sia rotatori (movimenti angolari attorno a specifici assi). Questo doppio movimento, noto come '''rototraslazione''', è fondamentale per comprendere la cinematica mandibolare. |
|
| |
|
| Questa sequenza di rotazioni consente di determinare in modo univoco l'orientamento del condilo nello spazio, evitando ambiguità derivanti dalla non-commutatività delle rotazioni angolari.
| | Per descrivere la posizione e il movimento di ciascun condilo nel tempo, si utilizzano vettori di posizione, che variano in modulo e direzione a seguito del moto elicoidale. Il moto è descritto da una combinazione di spostamenti lineari e variazioni angolari che influenzano la posizione dei vettori nello spazio tridimensionale. |
|
| |
|
| ----
| | '''Vettori di Posizione del Condilo Laterotrusivo (Lavorante)''' |
| '''Vettori di Posizione del Condilo Mediotrusivo (non lavorante)''' | |
|
| |
|
| Questo condilo si trova sul lato opposto rispetto al condilo lavorante e si sposta principalmente '''medialmente e anteriormente''' durante il movimento laterale della mandibola conosciuto nel gergo gnatologico come 'Condilo orbitante' ma contestualmente non meno complesso del lavorante. Il '''vettore di posizione''' del condilo mediotrusivo nel tempo è descritto da:
| | Il condilo laterotrusivo si trova sul lato in cui avviene la laterotrusione (spostamento laterale della mandibola). Durante il movimento, la sua posizione è descritta dal seguente vettore: |
|
| |
|
| <math> | | <math> |
| P_m(t) = [X_m(t), Y_m(t), Z_m(t), \theta_m(t), \phi_m(t), \psi_m(t)]
| | P_l(t) = [X_l(t), Y_l(t), Z_l(t), \theta_l(t), \phi_l(t), \psi_l(t)] |
| </math> | | </math> |
|
| |
|
| Dove: | | Dove: |
| *<math>X_m(t), Y_m(t), Z_m(t)</math>: Sono gli '''spostamenti lineari''' del condilo mediotrusivo: | | * <math>X_l(t), Y_l(t), Z_l(t)</math>: Spostamenti lineari lungo gli assi cartesiani: |
| **<math>X_m(t)</math>: Spostamento antero-posteriore. | | ** <math>X_l(t)</math>: Spostamento antero-posteriore. |
| **<math>Y_m(t)</math>: Spostamento latero-mediale. | | ** <math>Y_l(t)</math>: Spostamento latero-mediale. |
| **<math>Z_m(t)</math>: Spostamento verticale. | | ** <math>Z_l(t)</math>: Spostamento verticale. |
|
| |
|
| *<math>\theta_m(t), \phi_m(t), \psi_m(t)</math>: Descrivono le '''rotazioni angolari''' attorno ai tre assi: | | * <math>\theta_l(t)</math>, <math>\phi_l(t)</math>, <math>\psi_l(t)</math>: Rotazioni angolari attorno agli assi <math>X</math>, <math>Y</math> e <math>Z</math>, descritte con gli angoli di Eulero. |
| **<math>\theta_m(t)</math>: Rotazione attorno all'asse <math>x</math>.
| |
| **<math>\phi_m(t)</math>: Rotazione attorno all'asse <math>y</math>.
| |
| **<math>\psi_m(t)</math>: Rotazione attorno all'asse <math>z</math>.
| |
| <blockquote>Questa prima descrizione rappresenta solo il primo livello di complessità perchè i movimenti dei condili laterotrusivo e mediotrusivo si influenzano reciprocamente durante i cicli masticatori. Il condilo laterotrusivo esegue una rototraslazione lungo un arco che descrive una combinazione di rotazione attorno all'asse verticale <math>_vHA</math> ed uno spostamento laterale. Al contrario, il condilo mediotrusivo si sposta principalmente medialmente e anteriormente. Descriviamone la dinamica </blockquote>
| |
|
| |
|
| ==Rotazione del Condilo Laterotrusivo==
| | Adottiamo la convenzione <math>X,Y,Z</math>, che segue l’ordine: |
| La rotazione del condilo laterotrusivo attorno all'asse <math>Z</math> (verticale) è descritta matematicamente utilizzando una trasformazione lineare nel piano trasversale <math>(X, Y)</math>. Questa trasformazione è rappresentata dalla seguente matrice di rotazione:
| | * <math>\theta_l(t)</math>: Rotazione attorno a <math>X</math> (torsione laterale). |
| | * <math>\phi_l(t)</math>: Rotazione attorno a <math>Y</math> (apertura/chiusura). |
| | * <math>\psi_l(t)</math>: Rotazione attorno a <math>Z</math> (rotazione laterale/mediale). |
|
| |
|
| <math>
| | Questa sequenza consente una descrizione univoca dell’orientamento del condilo nello spazio. |
| R_\psi = \begin{pmatrix}
| |
| \cos(\psi) & -\sin(\psi) \\
| |
| \sin(\psi) & \cos(\psi)
| |
| \end{pmatrix}
| |
| \cdot
| |
| \begin{pmatrix}
| |
| X_L \\
| |
| Y_L
| |
| \end{pmatrix}
| |
| </math>
| |
|
| |
|
| Dove:
| | <gallery mode="slideshow"> |
| *<math>\psi</math> rappresenta l'angolo di rotazione attorno all'asse <math>Z</math> (asse verticale).
| | File:Sirignathograph rotazione asse Y.jpg|'''Figura 2:''' Tracciati cinematici masticatori sul piano sagittale. |
| *<math>(X_L, Y_L)</math> sono le coordinate del condilo laterotrusivo nel piano trasversale.
| | File:Sirognathograph frontal angle.jpg|'''Figura 3:''' Tracciati cinematici masticatori sul piano coronale. |
| | File:Final HA 10.jpg|'''Figura 4:''' Tracciati cinematici masticatori sul piano assiale. |
| | </gallery> |
|
| |
|
| Questo descrive il cambiamento di posizione del condilo laterotrusivo nel piano <math>(X, Y)</math> dovuto alla rotazione angolare.
| | '''Traslazione del Condilo Mediotrusivo''' |
|
| |
|
| ==Traslazione del Condilo Mediotrusivo==
| | Il condilo mediotrusivo, sul lato opposto al movimento laterale, si muove principalmente con una traslazione anteriore e mediale nello spazio tridimensionale. La traslazione è descritta dal seguente vettore: |
| Il condilo mediotrusivo si muove principalmente con una traslazione nello spazio tridimensionale, lungo i piani trasversale e sagittale, generando un tragitto noto come "tragitto orbitante". La traslazione è descritta dal seguente vettore: | |
|
| |
|
| <math> | | <math> |
| T_M(t) =\begin{pmatrix} | | T_M(t) = \begin{pmatrix} |
| X_M(t) \\ | | X_M(t) \\ |
| Y_M(t) \\ | | Y_M(t) \\ |
| Z_M(t) | | Z_M(t) |
| \end{pmatrix} | | \end{pmatrix} |
| </math>
| | </math> |
| | |
| Dove:
| |
| *<math>(X_M(t), Y_M(t), Z_M(t))</math> rappresentano le coordinate temporali del condilo mediotrusivo nello spazio cartesiano tridimensionale.
| |
| <blockquote>Questa traslazione rappresenta il movimento anteriore e mediale del condilo mediotrusivo. Inoltre, il condilo mediotrusivo può anche incorporare una rotazione attorno all'asse <math>Z</math> (asse verticale), influenzando significativamente la dinamica complessiva del ciclo masticatorio.
| |
| | |
| Da qui possiamo procedere con l'analisi combinata degli spostamenti lineari e angolari, descrivendo in modo completo il moto sia dei condili (laterotrusivo e mediotrusivo) che dei punti di riferimento principali come molare e incisivo.</blockquote> ==Descrizione delle misure lineari ed angolari==
| |
| | |
| ===Rappresentazione scalare dei tracciati condilari===
| |
| '''Descrizione delle distanze e delle direzioni'''
| |
| | |
| Di seguito sono riportate le distanze calcolate tra i punti rispetto al punto di partenza (punto 1) considerato il unto di riferimento essendo la mandibola in una posizione di Massima Intercuspidazione e le relative direzioni nello spazio, utilizzando le coordinate corrette per gli assi <math>X</math> (antero-posteriore) e <math>Y</math> (latero-mediale).
| |
| | |
| ==Calcolo delle distanze tra i punti==
| |
| | |
| **Coordinate dei punti:**
| |
| ***1L**: <math>(63.1721, -59.6914)</math>
| |
| ***2L**: <math>(62.9,-76.6) </math>
| |
| ***3L**: <math>(57.1, -108.3)</math>
| |
| ***4L**: <math>(56.5, -124.6)</math>
| |
| ***5L**: <math>(54.1, -93.3)</math>
| |
| ***6L**: <math>(54.7, -53.4)</math>
| |
| ***7L**: <math>(57.7,-50.8)</math>
| |
| ***8L**: <math>(60.2,-56.6)</math>
| |
| | |
| **Fattore di conversione:** <math>0.1007 \, \text{mm/pixel}</math>
| |
| | |
| **Distanze rispetto a 1L:**
| |
| ***2L**:
| |
| <math>d = \sqrt{(62.9 - 63.1721)^2 + (-76.6 - (-59.6914))^2} = \sqrt{(-0.2721)^2 + (-16.9086)^2} \approx 16.91 \, \text{pixel}</math>
| |
| <math>d = 16.91 \cdot 0.1007 \approx 1.70 \text{mm}</math>
| |
|
| |
|
| ***3L**:
| | Dove: |
| <math>d = \sqrt{(57.1 - 63.1721)^2 + (-108.3 - (-59.6914))^2} = \sqrt{(-6.0721)^2 + (-48.6086)^2} \approx 48.97 \, \text{pixel}</math> | | * <math>(X_M(t), Y_M(t), Z_M(t))</math>: Coordinate temporali del condilo mediotrusivo nello spazio cartesiano. |
| <math>d = 48.97 \cdot 0.1007 \approx 4.93 \text{mm}</math>
| |
|
| |
|
| ***4L**:
| | <blockquote>Questo tipo di traslazione influenza significativamente i tracciati occlusali, generando variazioni di orientamento durante il ciclo masticatorio.</blockquote> |
| <math>d = \sqrt{(56.5 - 63.1721)^2 + (-124.6 - (-59.6914))^2} = \sqrt{(-6.6721)^2 + (-64.9086)^2} \approx 65.25 \, \text{pixel}</math> | |
| <math>d = 65.25 \cdot 0.1007 \approx 6.57 \, \text{mm}</math>
| |
|
| |
|
| ***5L**:
| | == Descrizione delle misure lineari ed angolari == |
| <math>d = \sqrt{(54.1 - 63.1721)^2 + (-93.3 - (-59.6914))^2} = \sqrt{(-9.0721)^2 + (-33.6086)^2} \approx 34.81 \, \text{pixel}</math>
| |
| <math>d = 34.81 \cdot 0.1007 \approx 3.51 \, \text{mm}</math>
| |
|
| |
|
| ***6L**:
| | === Rappresentazione scalare dei tracciati condilari === |
| <math>d = \sqrt{(54.7 - 63.1721)^2 + (-53.4 - (-59.6914))^2} = \sqrt{(-8.4721)^2 + (6.2914)^2} \approx 10.64 \, \text{pixel}</math>
| |
| <math>d = 10.64 \cdot 0.1007 \approx 1.07 \, \text{mm}</math>
| |
|
| |
|
| ***7L**:
| | '''Descrizione delle distanze e delle direzioni''' |
| <math>d = \sqrt{(57.7 - 63.1721)^2 + (-50.8 - (-59.6914))^2} = \sqrt{(-5.4721)^2 + (8.8914)^2} \approx 10.45 \, \text{pixel}</math>
| |
| <math>d = 10.45 \cdot 0.1007 \approx 1.05 \, \text{mm}</math>
| |
|
| |
|
| ***8L**:
| | Di seguito sono riportate le distanze calcolate tra i punti rispetto al punto di partenza (punto 1, massima intercuspidazione), considerato punto di riferimento, e le relative direzioni nello spazio, utilizzando le coordinate corrette per gli assi <math>X</math> (antero-posteriore) e <math>Y</math> (latero-mediale). |
| <math>d = \sqrt{(60.2 - 63.1721)^2 + (-56.6 - (-59.6914))^2} = \sqrt{(-2.9721)^2 + (3.0914)^2} \approx 4.29 \, \text{pixel}</math> | |
| <math>d = 4.29 \cdot 0.1007 \approx 0.43 \, \text{mm}</math> | |
|
| |
|
| **Tabella riepilogativa:**
| | '''Calcolo delle distanze tra i punti''' |
| {| class="wikitable"
| |
| |+Distanze rispetto a 1L
| |
| |-
| |
| !Punto!! Distanza (pixel)!!Distanza (mm)
| |
| |-
| |
| |2L ||<math>16.91</math> ||<math>1.70</math>
| |
| |-
| |
| |3L||<math>48.97</math> ||<math>4.93</math>
| |
| |-
| |
| |4L||<math>65.25</math>||<math>6.57</math>
| |
| |-
| |
| |5L||<math>34.81</math>|| <math>3.51</math>
| |
| |-
| |
| |6L||<math>10.64</math>||<math>1.07</math>
| |
| |-
| |
| |7L|| <math>10.45</math>||<math>1.05</math>
| |
| |-
| |
| |8L||<math>4.29</math>||<math>0.43</math>
| |
| |}
| |
|
| |
|
| | Le coordinate dei punti estrapolate da Geogebra dopo calibrazione, per il condilo laterotrusivo, sono: |
| | * 1L: <math>(58.3, -50.9)</math> |
| | * 2L: <math>(59, -92.3)</math> |
| | * 3L: <math>(46.3, -169.5)</math> |
| | * 4L: <math>(44.1, -207.7)</math> |
| | * 5L: <math>(38.4, -136.2)</math> |
| | * 6L: <math>(36.4, -48.2)</math> |
| | * 7L: <math>(44, -34.9)</math> |
| | * 8L: <math>(52.9, -48)</math> |
|
| |
|
|
| |
|
| | '''Fattore di scala:''' <math>0.04184 \, \text{mm/pixel}</math> |
|
| |
|
| | Distanze rispetto a <math>1L_c</math>: |
|
| |
|
| e così via per le altre zone di misurazione.{{Tooltip|2=L'obiettivo dell'analisi è determinare l'angolo tra due movimenti all'interno di un sistema articolare, in particolare nell'area di studio della cinematica masticatoria. La comprensione di questi angoli ci consente di: '''Valutare la dinamica mandibolare''': Calcolare gli angoli tra i segmenti mandibolari può fornire informazioni essenziali su come la mandibola si sposta durante il movimento, aiutando a descrivere i pattern del movimento articolare. '''Modellare la biomeccanica del sistema masticatorio''': Gli angoli tra i punti permettono di costruire modelli accurati che simulano il comportamento meccanico del sistema mandibolare, utilizzabili in applicazioni cliniche per diagnosi e trattamenti. '''Confrontare con angoli standard''': Gli angoli misurati possono essere confrontati con valori normali o patologici per identificare eventuali alterazioni nei movimenti mandibolari che potrebbero indicare disturbi dell'articolazione temporomandibolare (ATM). Questo calcolo è fondamentale per fornire una descrizione matematica precisa della cinetica mandibolare e per migliorare la modellazione biomeccanica di strutture orofacciali, cruciali per la diagnosi e l'intervento clinico.}}<blockquote>A questo punto non ci resta altro da fare che rappresentare e simulare la posizione spaziale dei punti dinamici marcati dalla figura, quantificandone lo spostamento lineare ed angolare.</blockquote> == Distanze e Direzioni ==
| | '''<math>2L_c</math>:''' |
| ----
| |
|
| |
|
| ===Condilo Laterotrusivo=== | | <math>d = \sqrt{(59 - 58.3)^2 + (-92.3 - (-50.9))^2} = \sqrt{(0.7)^2 + (-41.4)^2} = \sqrt{0.49 + 1714.36} \approx 41.41 \, \text{pixel}</math> <math>d = 41.41 \cdot 0.04184 \approx 1.734 \, \text{mm}</math> |
| Questo paragrafo illustra un processo matematico utilizzato per calcolare la distanza e l'angolo formato tra due segmenti in un piano 2D, con applicazione nella cinematica mandibolare. La spiegazione riguarda come determinare l'angolo tra due vettori che rappresentano movimenti articolari all'interno di un sistema articolare, ad esempio i condili durante i movimenti della mandibola (Figura 2 e Tabella 1).
| |
|
| |
|
| <Center>
| | '''<math>3L_c</math>:''' |
| {|
| |
| ! colspan="5" |Tabella 1
| |
| |-
| |
| !Tracciato masticatorio
| |
| !Markers
| |
| !Distanza (mm)
| |
| !Direzione
| |
| (X - antero-posteriore)
| |
| !Direzione dinamica
| |
| (Y - latero-mediale)
| |
| |-
| |
| | rowspan="8" |[[File:Figura Condilo laterotrusico.jpg|center|400x400px|'''Figura 2:''' Rappresentazione grafica reale dei punti marcati nel ciclo masticatorio]]'''Figura 2''':
| |
| |2
| |
| |1.70
| |
| |Nessuno
| |
| |Lateralizzazione
| |
| |-
| |
| |3
| |
| |4.93
| |
| |Avanti
| |
| |Lateralizzazione
| |
| |-
| |
| |4
| |
| |6.57
| |
| |Avanti
| |
| |Lateralizzazione
| |
| |-
| |
| |5
| |
| |3.51
| |
| |Avanti
| |
| |Lateralizzazione
| |
| |-
| |
| |6
| |
| |1.07
| |
| |Indietro
| |
| |Medializzazione
| |
| |-
| |
| |7*
| |
| |1.05
| |
| |Indietro
| |
| |Medializzazione
| |
| |-
| |
| |8
| |
| |0.43
| |
| |Indietro
| |
| |Medializzazione
| |
| |-
| |
| | colspan="4" |
| |
| |}
| |
| </Center>
| |
|
| |
|
| Osservando la figura e la tabella, possiamo estrapolare le distanze dei punti marcati dallo strumento di replicazione dei movimenti mandibolari. Nello specifico, la distanza tra il punto <math>1L</math> e il punto <math>7L</math> è stata correttamente calcolata come circa <math>1.05 \, \text{mm}</math>, con una direzione calcolata come:
| | <math>d = \sqrt{(46.3 - 58.3)^2 + (-169.5 - (-50.9))^2} = \sqrt{(-12)^2 + (-118.6)^2} = \sqrt{144 + 14063.96} \approx 119.17 \, \text{pixel}</math> |
| <math>\theta = \arccos(0.840) \approx 33.57^\circ</math> | | <math>d = 119.17 \cdot 0.04184 \approx 4.99 \, \text{mm}</math> |
|
| |
|
| Per chi desidera approfondire il formalismo matematico, riportiamo il calcolo dettagliato nel popup interattivo.
| | '''<math>4L_c</math>:''' |
|
| |
|
| {{Tooltip|2=Dobbiamo calcolare la distanza euclidea tra i punti <math>P_1 = (63.1721, -59.6914)</math> e <math>P_7 = (57.7, -50.8)</math>. La formula per la distanza euclidea tra due punti <math>(x_1, y_1)</math> e <math>(x_2, y_2)</math> è:
| | <math>d = \sqrt{(44.1 - 58.3)^2 + (-207.7 - (-50.9))^2} = \sqrt{(-14.2)^2 + (-156.8)^2} = \sqrt{201.64 + 24589.44} \approx 157.43 \, \text{pixel}</math> |
| <math>\text{distanza} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.</math> '''Sostituendo i valori''': <math>\text{distanza} = \sqrt{(57.7 - 63.1721)^2 + (-50.8 - (-59.6914))^2}</math> <math>\text{distanza} = \sqrt{(-5.4721)^2 + (8.8914)^2} = \sqrt{29.96 + 79.06} = \sqrt{109.02} \approx 10.45 \, \text{pixel}.</math>. A questo punto, per convertire in millimetri, moltiplichiamo la distanza in pixel per il fattore di conversione: <math>\text{distanza in mm} = 10.45 \times 0.1007 \approx 1.05 \, \text{mm}.</math>
| | <math>d = 157.43 \cdot 0.04184 \approx 6.59 \, \text{mm}</math> |
| Ora possiamo calcolare l'angolo <math>\theta</math> utilizzando la formula per il coseno dell'angolo tra due vettori:
| |
| <math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}.</math> Infine, l'angolo <math>\theta</math> è calcolato tramite la funzione arccoseno: <math>\theta = \arccos(0.840) \approx 33.57^\circ.</math>}}
| |
| ===Molare Laterotrusivo===
| |
| Il testo descrive un'analisi dettagliata dei movimenti articolari del molare ipsilaterale al condilo laterotrusivo (Figura 3 e Tabella 2). L'analisi si basa sul calcolo delle distanze tra punti e degli angoli formati tra i vettori utilizzando la trigonometria vettoriale.
| |
|
| |
|
| <Center>
| | '''<math>5L_c</math>:''' |
| {|
| |
| ! colspan="5" |Tabella 2
| |
| |-
| |
| !Tracciato masticatorio
| |
| !Markers
| |
| !Distanza (mm)
| |
| !Direzione in X
| |
| (antero-posteriore)
| |
| !Direzione dinamica
| |
| (Y - latero-mediale)
| |
| |-
| |
| | rowspan="8" |[[File:Figura Molare laterotrusivo.jpg|center|400x400px|'''Figura 3:''' Rappresentazione delle distanze tra punti nel molare ipsilaterale alla laterotrusione]]
| |
| |2
| |
| |0.86
| |
| |Indietro
| |
| |Lateralizzazione
| |
| |-
| |
| |3
| |
| |5.47
| |
| |Indietro
| |
| |Lateralizzazione
| |
| |-
| |
| |4
| |
| |8.48
| |
| |Indietro
| |
| |Lateralizzazione
| |
| |-
| |
| |5
| |
| |13.52
| |
| |Indietro
| |
| |Lateralizzazione
| |
| |-
| |
| |6
| |
| |16.43
| |
| |Indietro
| |
| |Inversione
| |
| |-
| |
| |7*
| |
| |9.05
| |
| |Indietro
| |
| |Medializzazione
| |
| |-
| |
| |8
| |
| |2.72
| |
| |Indietro
| |
| |Medializzazione
| |
| |-
| |
| | colspan="4" |
| |
| |}
| |
| </Center>
| |
|
| |
|
| Osservando la figura e la tabella, possiamo estrapolare le distanze e le direzioni dei punti marcati. Nello specifico, la distanza del punto <math>7^*</math> rispetto al punto iniziale è stata calcolata come circa <math>9.05 \, \text{mm}</math>, con un angolo formato tra i vettori pari a <math>72.80^\circ</math>.
| | <math>d = \sqrt{(38.4 - 58.3)^2 + (-136.2 - (-50.9))^2} = \sqrt{(-19.9)^2 + (-85.3)^2} = \sqrt{396.01 + 7275.09} \approx 87.6 \, \text{pixel}</math> |
| | | <math>d = 87.6 \cdot 0.04184 \approx 3.66 \, \text{mm}</math> |
| {{Tooltip|2=**Iter matematico per il calcolo dell'angolo:**
| |
| * Il vettore tra il punto <math>P1_m</math> e il punto <math>P7_m</math>:
| |
| <math>\vec{AB} = P7_m - P1_m = (147.2, -380.7) - (185.2, -392.7) = (-38.0, 12.0)</math>
| |
| * Il vettore tra il punto <math>P1_m</math> e il punto di riferimento <math>R_p</math>:
| |
| <math>\vec{AC} = R_p - P1_m = (185.6, -308.9) - (185.2, -392.7) = (0.4, 83.8)</math>
| |
| | |
| Calcolo del coseno dell'angolo:
| |
| <math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}</math>
| |
| Sostituendo i valori:
| |
| <math>\cos(\theta) = \frac{990.4}{39.87 \cdot 83.80} \approx 0.2964</math>.
| |
| | |
| Infine, l'angolo <math>\theta</math> è calcolato tramite la funzione arccoseno:
| |
| <math>\theta = \arccos(0.2964) \approx 72.80^\circ</math>.}}==Incisal==
| |
| Il paragrafo caricato descrive un'analisi matematica dei movimenti articolari dell'incisivo sul lato lavorante. Utilizzando le coordinate di tre punti nello spazio 2D (\(P_1\), \(P_7\) e \(R_p\)), vengono calcolate le distanze lineari tra i punti, oltre all'angolo tra i segmenti che collegano questi punti.
| |
| | |
| <Center>
| |
| {|
| |
| ! colspan="5" | Tabella 3
| |
| |-
| |
| !Tracciato masticatorio
| |
| !Markers
| |
| !Distanza (mm)
| |
| !Direzione in X
| |
| (antero-posteriore)
| |
| !Direzione dinamica
| |
| (Y-latero-mediale)
| |
| |-
| |
| | rowspan="8" |[[File:Figura Incisal point.jpg|center|400x400px|Figura 3: Rappresentazione delle distanze tra punti dell'incisivo]]'''Figura 3:'''
| |
| | 2
| |
| |1.88
| |
| | Indietro
| |
| |Lateralizzazione
| |
| |-
| |
| |3
| |
| |3.84
| |
| |Indietro
| |
| |Lateralizzazione
| |
| |-
| |
| |4
| |
| |8.78
| |
| |Indietro
| |
| |Lateralizzazione
| |
| |-
| |
| |5
| |
| |14.71
| |
| |Indietro
| |
| |Lateralizzazione
| |
| |-
| |
| |6
| |
| |19.34
| |
| |Indietro
| |
| |Inversione
| |
| |-
| |
| |7*
| |
| |13.42
| |
| |Indietro
| |
| |Medializzazione
| |
| |-
| |
| |8
| |
| |2.57
| |
| |Indietro
| |
| |Medializzazione
| |
| |-
| |
| | colspan="4" |
| |
| |}
| |
| </Center>
| |
| | |
| Per quanto riguarda i tracciati nell'area dell'incisivo tra il punto <math>P_1</math> e <math>P_7</math>, la distanza risulta essere di **13.42 mm** con un angolo approssimativamente pari a **82°**. Per approfondimenti di calcolo, vedi la spiegazione dettagliata qui sotto.
| |
| | |
| {{Tooltip|2=Coordinate dei punti: <math>P_1 = (305.4, -520.0)</math>, <math>P_7 = (257.5, -515.7)</math>, <math>R_p = (305.4, -439.3)</math>. Il vettore tra <math>P_1</math> e <math>P_7</math> è: <math>\vec{AB} = P_7 - P_1 = (257.5, -515.7) - (305.4, -520.0) = (-47.9, 4.3)</math>. Il vettore tra <math>P_1</math> e <math>R_p</math> è: <math>\vec{AC} = R_p - P_1 = (305.4, -439.3) - (305.4, -520.0) = (0, 80.7)</math>. Il prodotto scalare tra i vettori è calcolato come: <math>\vec{AB} \cdot \vec{AC} = AB_x \cdot AC_x + AB_y \cdot AC_y = (-47.9) \cdot 0 + (4.3) \cdot (80.7) = 0 + 347.01 = 347.01</math>. Le norme dei vettori sono: <math>|\vec{AB}| = \sqrt{(-47.9)^2 + (4.3)^2} = \sqrt{2294.41 + 18.49} = \sqrt{2312.90} \approx 48.10</math> e <math>|\vec{AC}| = \sqrt{(0)^2 + (80.7)^2} = \sqrt{0 + 6508.49} = \sqrt{6508.49} \approx 80.7</math>. Il coseno dell'angolo tra i vettori è dato da: <math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|} = \frac{347.01}{48.10 \cdot 80.7} = \frac{347.01}{3879.87} \approx 0.0895</math>. Infine, l'angolo è: <math>\theta = \arccos(0.0895) \approx 82^\circ</math>.}}
| |
| | |
| Infine, l'angolo è:
| |
| <nowiki><math>\theta = Il risultato lineare ed angolare è di **13.42 mm** rispetto al punto golare è di **1 e con un angolo approssimativamente pari a **82°**.}}</nowiki>==Molare controlaterale==
| |
| | |
| Osservando il moto cinematico mandibolare a livello del molare mediotrusivo, si nota come cambia sia la direzione (angolo rispetto all'asse perpendicolare che interseca il punto 1 del condilo mediotrusivo) sia la medializzazione nel ritorno allo stato iniziale, che corrisponde sostanzialmente allo svincolo mediotrusivo tra la cuspide centrale e distale del primo molare.
| |
| | |
| <Center>
| |
| {|
| |
| ! colspan="5" |Tabella 4
| |
| |-
| |
| !Tracciato masticatorio
| |
| !Markers
| |
| !Distanza
| |
| (mm)
| |
| !Direzione in X
| |
| (antero-posteriore)
| |
| !Direzione
| |
| dinamica
| |
| | |
| (Y -latero-mediale)
| |
| |-
| |
| | rowspan="11" |[[File:Figura molare mediotrusivo.jpg|center|400x400px|'''Figura 4:''']]'''Figura 4:'''
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |-
| |
| |2||1.11
| |
| |Avanti||Medializzazione
| |
| |-
| |
| |3||3.89
| |
| |Avanti||Medializzazione
| |
| |-
| |
| |4||7.76
| |
| |Avanti||Medializzazione
| |
| |-
| |
| |5||13.75
| |
| |Avanti||Medializzazione
| |
| |-
| |
| |6||15.71
| |
| |Indietro||Inversione
| |
| |-
| |
| |7*||8.99
| |
| |Indietro||Lateralizzazione
| |
| |-
| |
| |8||2.43
| |
| |Indietro||Lateralizzazione
| |
| |-
| |
| | colspan="4" |
| |
| |}
| |
| </Center>
| |
| | |
| <br />
| |
| | |
| Come per i precedenti, la distanza lineare tra il punto 1 ed il punto 7* è risultata essere <math>8.99</math> mm e l'angolo <math>\theta</math> è calcolato tramite la funzione arcoseno: <math>\theta = \arccos(-0.0232) \approx 91.33^\circ</math>.
| |
| | |
| Per approfondire la procedura matematica vedi {{Tooltip|2=I tre punti nello spazio 2D sono <math>P1_{mm}</math> (punto 1 del molare mediotrusivo), <math>P7_{mm}</math> (punto 7 del molare mediotrusivo) e <math>R_p</math> (punto di riferimento), con coordinate <math>P1_{mm} = (422.5, -396.1)</math>, <math>P7_{mm} = (383.8, -395.1)</math>, <math>R_p = (422.7, -336.6)</math>. Il vettore tra <math>P1_{mm}</math> e <math>P7_{mm}</math> è <math>\vec{AB} = (-38.7, 1.0)</math>, mentre il vettore tra <math>P1_{mm}</math> e <math>R_p</math> è <math>\vec{AC} = (0.2, 59.5)</math>. Prodotto scalare: <math>\vec{AB} \cdot \vec{AC} = (-38.7) \cdot (0.2) + (1.0) \cdot (59.5) = -7.74 + 59.5 = 51.76</math>. Norme: <math>|\vec{AB}| = \sqrt{(-38.7)^2 + (1.0)^2} = \sqrt{1498.69 + 1.0} = \sqrt{1499.69} \approx 38.73</math>, <math>|\vec{AC}| = \sqrt{(0.2)^2 + (59.5)^2} = \sqrt{0.04 + 3540.25} = \sqrt{3540.29} \approx 59.54</math>. Coseno: <math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|} = \frac{51.76}{38.73 \cdot 59.54} \approx 0.0226</math>. Angolo: <math>\theta = \arccos(0.0226) \approx 91.33^\circ</math>. Distanza lineare: <math>d = \sqrt{1499.69} \approx 38.73 \, \text{pixel}</math>, convertita in millimetri: <math>d = 38.73 \cdot 0.1 = 8.99 \, \text{mm}</math>.}}===Condilo Mediotrusivo===
| |
| | |
| Questi punti rappresentano tre posizioni specifiche all'interno di un sistema articolare che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti <math>P1_{M}</math> e <math>P7_{M}</math>, e il segmento che unisce i punti <math>P1_{M}</math> e <math>R_p</math>. Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio.
| |
| | |
| | |
| | |
| ----
| |
| ===Condilo Mediotrusivo===
| |
| | |
| Questi punti rappresentano tre posizioni specifiche all'interno di un sistema articolare che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti <math>P1_{M}</math> e <math>P7_{M}</math>, e il segmento che unisce i punti <math>P1_{M}</math> e <math>R_p</math>. Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio.
| |
| | |
| <Center>
| |
| {|
| |
| ! colspan="5" |Tabella 5
| |
| |-
| |
| !Tracciato masticatorio
| |
| !Markers!!Distanza (mm)!!Direzione in X (antero-posteriore)!!Direzione (Y-latero-mediale)
| |
| |-
| |
| | rowspan="8" |[[File:Figura condilo mediotrusivo mod..jpg|center|408x408px]]'''Figura 5:'''
| |
| |2||5.09||Protrusiva||Medializzazione
| |
| |-
| |
| |3||14.81||Protrusiva||Medializzazione
| |
| |-
| |
| |4||25.58||Protrusiva||Medializzazione
| |
| |-
| |
| |5||26.54||Protrusiva||Inversione
| |
| |-
| |
| |6||14.57||Protrusiva||Lateralizzazione
| |
| |-
| |
| |7*||6.25||Protrusiva||Lateralizzazione
| |
| |-
| |
| |8||1.19||Protrusiva||Lateralizzazione
| |
| |-
| |
| | colspan="4" |
| |
| |}
| |
| </Center>
| |
| | |
| Per quanto riguarda le distanze e la direzione del punto 7 nel condilo mediotrusivo abbiamo una distanza dal punto di partenza di 6.25 mm ed un angolo calcolato sull'arcoseno <math>\theta = \arccos(-0.971) \approx 166^\circ</math>. Infine, sottraendo questo angolo da 180°, otteniamo un angolo di <math>13.57^\circ</math>, noto come '''Angolo di Bennett'''. Per approfondire la procedura matematica vedi {{Tooltip|2=L'angolo tra due segmenti può essere calcolato utilizzando la trigonometria vettoriale. Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti: il vettore tra il punto <math>P1_{M}</math> e il punto <math>P7_{M}</math>: <math>\vec{AB} = P7_{M}-P1_{M}=(522.5, -87)-(530.6, -61.8)=(-8.1, -25.2)</math>. Il vettore tra il punto <math>P1_{M}</math> e il punto di riferimento <math>R_p</math>: <math>\vec{AC}=R_p-P1_{M}=(530.8, -9.3)-(530.6, -61.8)=(0.2, 52.5)</math>. Il prodotto scalare tra i vettori <math>\vec{AB}</math> e <math>\vec{AC}</math> è dato dalla formula: <math>\vec{AB} \cdot \vec{AC} = AB_x \cdot AC_x + AB_y \cdot AC_y</math>. Sostituendo i valori calcolati: <math>\vec{AB} \cdot \vec{AC} = (-8.1) \cdot (0.2) + (-25.2) \cdot (52.5) = -1.62 - 1323.0 = -1324.62</math>. Le norme dei vettori sono: <math>|\vec{AB}| = \sqrt{(-8.1)^2 + (-25.2)^2} = \sqrt{65.61 + 635.04} = \sqrt{700.65} \approx 26.47</math> e <math>|\vec{AC}| = \sqrt{(0.2)^2 + (52.5)^2} = \sqrt{0.04 + 2756.25} = \sqrt{2756.29} \approx 52.50</math>. Ora possiamo usare la formula per il coseno dell'angolo tra i due vettori: <math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}</math>. Sostituendo i valori: <math>\cos(\theta) = \frac{-1324.62}{26.47 \cdot 52.50} = \frac{-1324.62}{1388.68} \approx -0.971</math>. L'angolo <math>\theta</math> è calcolato tramite la funzione arccoseno: <math>\theta = \arccos(-0.971) \approx 166.43^\circ</math>. Infine, sottraendo questo angolo da 180°, otteniamo un angolo di <math>13.57^\circ</math>, noto come '''Angolo di Bennett'''.}} == Conclusione Integrata: Il Peso dei Condili e il Ruolo dei Tracciati Occlusali ==
| |
| | |
| L’analisi delle traiettorie mandibolari evidenzia una complessa interazione tra movimenti lineari e angolari. Questi movimenti, rilevati nei punti chiave della mandibola, riflettono l'equilibrio tra stabilità e adattabilità dinamica durante la funzione masticatoria. La combinazione dei pesi lineari e angolari offre una visione integrata del contributo relativo di ogni punto articolare, fornendo una base interpretativa robusta per il bilanciamento occlusale.
| |
| | |
| === Tabella Riassuntiva dei Pesi ===
| |
| | |
| {| class="wikitable"
| |
| |+ **Contributo Lineare e Angolare ai Tracciati Occlusali**
| |
| |-
| |
| ! Area Analizzata !! Distanza (mm) !! Angolo Calcolato (°) !! Reciproco (°) !! Peso Lineare (%) !! Peso Angolare (%) !! Peso Combinato (%)
| |
| |-
| |
| | Condilo Laterotrusivo || 3.16 || 33.57 || 146.43 || 7.8 || 16.7 || 12.3
| |
| |-
| |
| | Molare Laterotrusivo || 9.10 || 72.80 || 107.20 || 22.4 || 12.2 || 17.3
| |
| |-
| |
| | Incisivo || 13.84 || 82.00 || 98.00 || 34.1 || 11.2 || 22.7
| |
| |-
| |
| | Molare Mediotrusivo || 8.99 || 91.33 || 88.67 || 22.1 || 10.1 || 16.1
| |
| |-
| |
| | Condilo Mediotrusivo || 6.25 || 166.00 || 14.00 || 15.4 || 49.8 || 32.6
| |
| |}
| |
| | |
| === Metodo di Calcolo dei Pesi ===
| |
| | |
| Il peso combinato tiene conto di due parametri fondamentali:
| |
| | |
| # Peso Lineare: Determinato dalla distanza percorsa dal punto analizzato rispetto al punto di riferimento (solitamente <math>P_1</math>).
| |
| # Peso Angolare: Calcolato come la normalizzazione dell'angolo reciproco rispetto alla somma di tutti i reciproci degli angoli analizzati.
| |
| | |
| I pesi relativi sono ottenuti mediante la seguente procedura:
| |
| | |
| Peso Lineare Normalizzato:
| |
| | |
| <math>P_L = \frac{\text{Distanza del punto}}{\text{Somma di tutte le distanze}}</math>.
| |
| | |
| Peso Angolare Normalizzato:
| |
| | |
| <math>P_A = \frac{\text{Reciproco dell'angolo del punto}}{\text{Somma di tutti i reciproci degli angoli}}</math>. | |
| | |
| Peso Combinato:
| |
| | |
| <math>P_C = 0.5 \cdot P_L + 0.5 \cdot P_A</math>, per dare, in questo contesto, pari importanza alle componenti lineari e angolari.
| |
| | |
| === Considerazioni Finali ===
| |
| | |
| Condilo Laterotrusivo (Lavorante)**
| |
| Con una distanza percorsa relativamente ridotta (3.16 mm) e un angolo di 33.57° (reciproco di 146.43°), il condilo laterotrusivo evidenzia un peso combinato del 12.3%. Questo sottolinea il suo ruolo stabilizzatore durante i movimenti laterali, caratterizzato da un'azione vincolata e guidata sul lato lavorante.
| |
| | |
| Molare Laterotrusivo: La distanza di 9.10 mm e l’angolo di 72.80° (reciproco di 107.20°) assegnano al molare laterotrusivo un peso combinato del 17.3%. Questo riflette la sua rilevanza nel definire i tracciati occlusali laterali, in stretta interazione con il condilo lavorante. Incisivo: Con la maggiore distanza percorsa (13.84 mm) e un angolo di 82.00° (reciproco di 98.00°), l'incisivo presenta il peso combinato più alto tra i denti (22.7%). Questo conferma il suo ruolo dominante nel bilanciare i movimenti mandibolari anteriori e laterali. Molare Mediotrusivo (Controlaterale): Il molare mediotrusivo, con una distanza di 8.99 mm e un angolo di 91.33° (reciproco di 88.67°), ha un peso combinato del 16.1%. Questo dimostra la sua funzione di supporto nella distribuzione delle forze laterali e nella stabilizzazione della traiettoria masticatoria. Condilo Mediotrusivo (Non Lavorante): Nonostante la distanza ridotta (6.25 mm), il condilo mediotrusivo presenta il comportamento angolare più marcato (166.00°, reciproco di 14.00°). Con un peso combinato del 32.6%, enfatizza la sua funzione compensatoria, essenziale per la dinamica orbitale e per mantenere l’equilibrio articolare.
| |
| | |
| L’analisi dei pesi combinati permette di quantificare il contributo specifico dei condili e dei denti alla funzione occlusale, fornendo una visione integrata dei movimenti mandibolari. Questo approccio può essere esteso a modelli clinici per prevedere disfunzioni o pianificare trattamenti personalizzati, migliorando la comprensione biomeccanica della funzione masticatoria.
| |
| | |
| {{Rosso inizio}}qui {{Rosso Fine}}
| |
| | |
|
| |
| [[File:Question 2.jpg|left|100x100px]]
| |
| ----
| |
| ==C==
| |
| ----
| |
| ==La scelta della conica a 5 punti==
| |
| La scelta di una conica a 5 punti rappresenta un approccio matematico e geometrico efficace per modellare i tracciati articolari reali rispetto a un'ellisse ideale.
| |
| | |
| ===Definizione della conica===
| |
| Una conica è una curva definita in geometria analitica come il luogo dei punti che soddisfano un'equazione quadratica generale:
| |
| <math> A x^2 + B x y + C y^2 + D x + E y + F = 0 </math>
| |
| | |
| Dove:
| |
| * <math> A, B, C, D, E, F </math> sono coefficienti reali determinati dai punti dati.
| |
| * La forma della conica (ellisse, parabola o iperbole) dipende dal discriminante:
| |
| * **Ellisse** se <math> B^2 - 4 A C < 0 </math>
| |
| * **Parabola** se <math> B^2 - 4 A C = 0 </math>
| |
| * **Iperbole** se <math> B^2 - 4 A C > 0 </math>
| |
| | |
| ===Perché 5 punti?===
| |
| Una conica è univocamente determinata da **5 punti distinti non allineati**. Questo significa che se conosci 5 punti sperimentali, puoi ricostruire una sola conica che passa per quei punti.
| |
| | |
| ===Proprietà principali===
| |
| * **Univocità**: La conica è unica per 5 punti non allineati.
| |
| * **Adattabilità**: Si adatta meglio ai dati sperimentali rispetto a un'ellisse ideale.
| |
| * **Flessibilità**: Modella tracciati complessi, asimmetrici o irregolari, tipici della cinematica mandibolare.
| |
| | |
| ===Costruzione delle coniche specifiche===
| |
| Abbiamo costruito coniche specifiche per diverse aree della traiettoria mandibolare.
| |
| | |
| ====Conica del molare laterotrusivo====
| |
| La conica è stata costruita utilizzando 5 punti chiave lungo il tracciato sperimentale del **molare laterotrusivo**:
| |
| * <math> P_1 = (149.24, -380.71) </math>
| |
| * <math> P_2 = (187.30, -392.66) </math>
| |
| * <math> P_3 = (526.04, -87.36) </math>
| |
| * <math> P_4 = (530.57, -61.83) </math>
| |
| * <math> P_5 = (60.13, -51.29) </math>
| |
| | |
| ====Conica dell'incisivo====
| |
| La conica è stata determinata utilizzando punti significativi lungo la traiettoria reale dell'**incisivo**:
| |
| * <math> P_1 = (257.81, -513.52) </math>
| |
| * <math> P_2 = (305, -520) </math>
| |
| * <math> P_3 = (526.04, -87.36) </math>
| |
| * <math> P_4 = (530.57, -61.83) </math>
| |
| * <math> P_5 = (60.13, -51.29) </math>
| |
| | |
| ====Conica del molare mediotrusivo====
| |
| La conica è stata generata per il **molare mediotrusivo** usando i seguenti punti chiave:
| |
| * <math> P_1 = (383.79, -396.65) </math>
| |
| * <math> P_2 = (422.45, -396.15) </math>
| |
| * <math> P_3 = (526.04, -87.36) </math>
| |
| * <math> P_4 = (530.57, -61.83) </math>
| |
| * <math> P_5 = (60.13, -51.29) </math>
| |
| | |
| ===Costruzione della conica unificata===
| |
| Per ottenere una visione complessiva, abbiamo calcolato una **conica unificata** a partire dalle coniche specifiche. Questa conica è stata costruita mediando i coefficienti delle coniche delle diverse aree:
| |
| <math>
| |
| \text{Coefficienti Conica Unificata} = \frac{\text{Coeff}_\text{molare laterotrusivo} + \text{Coeff}_\text{incisale} + \text{Coeff}_\text{molare mediotrusivo}}{3} | |
| </math> | |
|
| |
|
| L'equazione risultante è:
| | '''<math>6L_c</math>:''' |
| <math> | |
| 5.0308e-05 \, x^2 + 1.5429e-05 \, x y + 3.1889e-06 \, y^2 - 0.02901 \, x - 0.01175 \, y + 0.99918 = 0
| |
| </math> | |
| [[File:Figura Conica.jpg|center|thumb|300x300px]]
| |
|
| |
|
| ===Applicazione della conica per individuare punti cinematici=== | | <math>d = \sqrt{(36.4 - 58.3)^2 + (-48.2 - (-50.9))^2} = \sqrt{(-21.9)^2 + (2.7)^2} = \sqrt{479.61 + 7.29} \approx 22.06 \, \text{pixel}</math> |
| Utilizzando la conica del molare laterotrusivo, è possibile **prevedere il punto C_L(7)** (condilo laterotrusivo) conoscendo due punti di riferimento (es. punto iniziale e finale sul tracciato molare). Questo approccio permette di:
| | <math>d = 22.06 \cdot 0.04184 \approx 0.923 \, \text{mm}</math> |
| * Determinare con precisione **dove cade il punto condilare laterotrusivo** sulla conica.
| |
| * Utilizzare la conica come strumento per analizzare deviazioni e adattamenti nei tracciati mandibolari reali.
| |
|
| |
|
| ===Riflessioni finali===
| | '''<math>7L_c</math>:''' |
| La costruzione delle coniche a 5 punti ha permesso di modellare con precisione i tracciati:
| |
| 1. **Molare laterotrusivo**
| |
| 2. **Incisivo**
| |
| 3. **Molare mediotrusivo**
| |
|
| |
|
| L'uso della **conica unificata** ha offerto una visione globale, ma per una maggiore precisione, le **coniche specifiche** risultano più adatte per localizzare punti chiave come il punto C_L(7).
| | <math>d = \sqrt{(44 - 58.3)^2 + (-34.9 - (-50.9))^2} = \sqrt{(-14.3)^2 + (16)^2} = \sqrt{204.49 + 256} \approx 21.47 \, \text{pixel}</math> |
| | <math>d = 21.47 \cdot 0.04184 \approx 0.898 \, \text{mm}</math> |
|
| |
|
| ===Prossimi passi===
| | '''<math>8L_c</math>:''' |
| * Approfondire l'uso della conica per prevedere tracciati mancanti o deviazioni nei movimenti articolari.
| |
| * Validare le coniche con dati sperimentali aggiuntivi.
| |
| * Studiare il comportamento delle coniche in relazione ai movimenti condilari mediotrusivi e laterotrusivi.
| |
|
| |
|
| | <math>d = \sqrt{(52.9 - 58.3)^2 + (-48 - (-50.9))^2} = \sqrt{(-5.4)^2 + (2.9)^2} = \sqrt{29.16 + 8.41} \approx 6.13 \, \text{pixel}</math> |
|
| |
|
| <br /> | | <math>d = 6.13 \cdot 0.04184 \approx 0.257 \, \text{mm}</math> |
Introduzione
Nel capitolo precedente, 'Transverse Hinge Axis', abbiamo introdotto la cinematica mandibolare concentrandoci sul piano sagittale. Durante i movimenti di protrusione e retrusione, la mandibola non si muove esclusivamente lungo l'asse  , ma ruota attorno al centro dell'asse
, ma ruota attorno al centro dell'asse  . Questo movimento condilare si manifesta anteriormente, dove l'incisivo mandibolare segue traiettorie curvilinee inverse, risultato di un complesso moto spaziale generato dalla rototraslazione sugli assi condilari. Lo spazio angolare risultante, noto come 'Spazio libero Interincisivo', è essenziale per consentire movimenti masticatori fluidi e senza ostacoli.
. Questo movimento condilare si manifesta anteriormente, dove l'incisivo mandibolare segue traiettorie curvilinee inverse, risultato di un complesso moto spaziale generato dalla rototraslazione sugli assi condilari. Lo spazio angolare risultante, noto come 'Spazio libero Interincisivo', è essenziale per consentire movimenti masticatori fluidi e senza ostacoli.
Questo 'Spazio libero Interincisivo' riveste un ruolo cruciale nelle funzioni masticatorie. Tuttavia, strumenti come il Sirognatograph e i sistemi elettromagnetici tradizionali trascurano la componente rotazionale dei movimenti condilari, focalizzandosi principalmente sulle traslazioni. Sebbene ciò possa essere sufficiente per alcune registrazioni, tale approccio è limitato nel cogliere la complessità dei movimenti mandibolari a sei gradi di libertà.
Cinematica Mandibolare a Sei Gradi di Libertà
Il movimento mandibolare avviene in uno spazio tridimensionale e può essere descritto come un complesso moto spaziale. Ogni condilo è associato a tre assi principali:
- Asse
 (latero-mediale): Definisce la rotazione attorno all'asse cerniera trasversale (
(latero-mediale): Definisce la rotazione attorno all'asse cerniera trasversale ( , transverse Hinge Axis).
, transverse Hinge Axis).
- **Asse
 (verticale):** Definisce la rotazione sull'asse cerniera verticale (
(verticale):** Definisce la rotazione sull'asse cerniera verticale ( ).
).
- **Asse
 (antero-posteriore): Definisce la rotazione attorno all'asse cerniera orizzontale (
(antero-posteriore): Definisce la rotazione attorno all'asse cerniera orizzontale ( ).
).
A ciascun asse corrisponde un piano di riferimento anatomico:
- Piano sagittale: Mostra il tracciato condilare prodotto dal movimento di rototraslazione dell'asse trasversale (
 ).
).
- Piano coronale: Associato all'asse orizzontale (
 ).
).
- Piano assiale: Legato al movimento generato attorno all'asse verticale (
 , noto anche come asse cerniera verticale).
, noto anche come asse cerniera verticale).
Va evidenziato che un piano non è generato da un asse; un asse può al massimo essere contenuto in un piano o rappresentare una direzione. Più precisamente, il movimento di un asse genera una 'superficie rigata', che descrive le traiettorie spaziali risultanti.
Asse cerniera verticale
Ci concentreremo sull’asse cerniera verticale ( ) per la sua rilevanza nei sistemi di registrazione cinematici come pantografi, elegnatografi e assiografi. Tuttavia, è necessario esaminare il razionale della Gnatologia Classica per comprendere l'interazione tra piani e assi nel descrivere i movimenti condilari.
) per la sua rilevanza nei sistemi di registrazione cinematici come pantografi, elegnatografi e assiografi. Tuttavia, è necessario esaminare il razionale della Gnatologia Classica per comprendere l'interazione tra piani e assi nel descrivere i movimenti condilari.
- Il pantografo analogico è stato considerato un dispositivo capace di riprodurre con precisione i movimenti di confine dei tracciati condilari e di trasferirli su un articolatore completamente regolabile tramite le sue 6 piastrine.[1][2][3]
- Successivamente, si è riportato che anche il pantografo elettronico registrava i determinanti condilari con un intervallo accettabile (argomento trattato nei capitoli successivi).[4]
- Un determinante particolare del movimento condilare, la traslazione laterale immediata mandibolare (Movimento di Bennett), è stato oggetto di dibattito e confusione nella letteratura protesica.[5] Tuttavia, una recente revisione della letteratura ha evidenziato una mancanza di prove sul significato clinico di questo movimento.[6]
Nota sulla Precisione e Sugli Obiettivi dello Studio
Questo studio mira a fornire una comprensione concettuale dei principi cinematici coinvolti nella dinamica masticatoria, con un focus sulla biomeccanica mandibolare. Sebbene i calcoli siano stati eseguiti con rigore, potrebbero verificarsi discrepanze dovute a:
- Approssimazioni nei dati numerici: Differenze nei valori cartesiani legate a variabili operative.
- Limiti di rappresentazione: Uso di numeri approssimati per motivi pratici.
- Finalità cliniche: Lo scopo è descrivere concetti piuttosto che ottenere precisione assoluta.
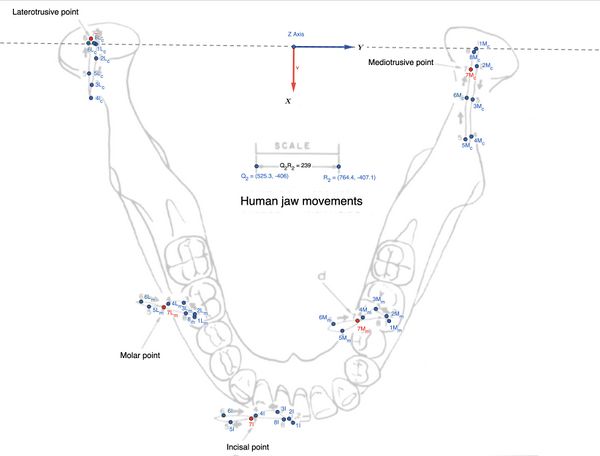
Figura 1: Cinematica mandibolare sul piano assiale rappresentata dai markers prelevati dallo strumento ogni 20 mSec. Questi punti rappresentano i condili laterotrusivi dal punto  e mediotrusivi
e mediotrusivi  . Il Laterotrusive point (a sinistra) e il Mediotrusive point (a destra) tracciano la posizione dei condili della mandibola durante un movimento masticatorio laterale, che include movimenti complessi di traslazione e rotazione. I punti numerati (
. Il Laterotrusive point (a sinistra) e il Mediotrusive point (a destra) tracciano la posizione dei condili della mandibola durante un movimento masticatorio laterale, che include movimenti complessi di traslazione e rotazione. I punti numerati ( ....
.... ) seguono il movimento del condilo laterotrusivo nel tempo, mentre i punti
) seguono il movimento del condilo laterotrusivo nel tempo, mentre i punti  ....
.... seguono il condilo mediotrusivo. Nell'area del Molar point e dell' Incisal point sono rappresentati i percorsi occlusali durante la masticazione.
seguono il condilo mediotrusivo. Nell'area del Molar point e dell' Incisal point sono rappresentati i percorsi occlusali durante la masticazione. Passi Successivi
In questo capitolo, analizzeremo la cinematica dell'asse verticale ( ) e il fenomeno masticatorio, rappresentandolo con tracciati estratti da lavori di riferimento come quello di Lund e Gibbs.[7](Figura 1)
) e il fenomeno masticatorio, rappresentandolo con tracciati estratti da lavori di riferimento come quello di Lund e Gibbs.[7](Figura 1)
Descrizione della Calibrazione: da Pixel a Millimetri
La calibrazione di un'immagine per ottenere misurazioni accurate richiede l'attenzione a diversi fattori critici. Estrarre distanze da un'immagine può essere complesso, poiché la precisione dipende da:
- Fattori di distorsione: Le immagini possono essere affette da distorsioni ottiche, che devono essere corrette calibrando la camera utilizzando, ad esempio, una scacchiera di riferimento.
- Effetto prospettico: La scala di riferimento varia con la distanza dal piano di acquisizione. Per oggetti posti a diverse profondità, è necessario applicare fattori di scala specifici, calcolati utilizzando un modello come quello della pin-hole camera.
- Distorsioni prospettiche: Queste possono essere corrette utilizzando ottiche telecentriche, particolarmente utili per applicazioni che richiedono un'elevata accuratezza, come nelle misurazioni spaziali o bioingegneristiche.
Con questa premessa, il fattore di scala utilizzato nel nostro studio rappresenta un'approssimazione valida nel contesto specifico delle immagini 2D acquisite in condizioni controllate. Tuttavia, per applicazioni più rigorose, come quelle descritte sopra, è necessario considerare strumenti e metodi avanzati per la calibrazione.
Calcolo della Distanza tra i Punti
Le coordinate dei punti sono:
 e
e 
La formula per la distanza euclidea è:

Sostituendo i valori:



Conversione della Scala in mm
Dato che il segmento di  equivale a
equivale a  , calcoliamo la conversione in mm/pixel:
, calcoliamo la conversione in mm/pixel:

Quindi, ogni pixel nella figura corrisponde a circa:
 .
.
Esempio di Applicazione: Conversione Distanza in mm
Supponiamo di voler calcolare una distanza in mm. Ad esempio, se la distanza in pixel fosse  :
:

Risultato Finale
La scala è:


Questi valori possono essere usati per convertire qualsiasi distanza misurata in pixel nella figura in unità metriche come millimetri o centimetri.
Cinematica dei Condili
Traslazioni e Rotazioni dei Condili
Nel contesto del movimento mandibolare, i condili eseguono sia movimenti traslatori (spostamenti lineari) sia rotatori (movimenti angolari attorno a specifici assi). Questo doppio movimento, noto come rototraslazione, è fondamentale per comprendere la cinematica mandibolare.
Per descrivere la posizione e il movimento di ciascun condilo nel tempo, si utilizzano vettori di posizione, che variano in modulo e direzione a seguito del moto elicoidale. Il moto è descritto da una combinazione di spostamenti lineari e variazioni angolari che influenzano la posizione dei vettori nello spazio tridimensionale.
Vettori di Posizione del Condilo Laterotrusivo (Lavorante)
Il condilo laterotrusivo si trova sul lato in cui avviene la laterotrusione (spostamento laterale della mandibola). Durante il movimento, la sua posizione è descritta dal seguente vettore:
![{\displaystyle P_{l}(t)=[X_{l}(t),Y_{l}(t),Z_{l}(t),\theta _{l}(t),\phi _{l}(t),\psi _{l}(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0460bad60fdbd2bf924fac810d7383a682d79d9e)
Dove:
 : Spostamenti lineari lungo gli assi cartesiani:
: Spostamenti lineari lungo gli assi cartesiani:
 : Spostamento antero-posteriore.
: Spostamento antero-posteriore. : Spostamento latero-mediale.
: Spostamento latero-mediale. : Spostamento verticale.
: Spostamento verticale.
 ,
,  ,
,  : Rotazioni angolari attorno agli assi
: Rotazioni angolari attorno agli assi  ,
,  e
e  , descritte con gli angoli di Eulero.
, descritte con gli angoli di Eulero.
Adottiamo la convenzione  , che segue l’ordine:
, che segue l’ordine:
 : Rotazione attorno a
: Rotazione attorno a  (torsione laterale).
(torsione laterale). : Rotazione attorno a
: Rotazione attorno a  (apertura/chiusura).
(apertura/chiusura). : Rotazione attorno a
: Rotazione attorno a  (rotazione laterale/mediale).
(rotazione laterale/mediale).
Questa sequenza consente una descrizione univoca dell’orientamento del condilo nello spazio.
Figura 2: Tracciati cinematici masticatori sul piano sagittale.
Figura 3: Tracciati cinematici masticatori sul piano coronale.
Figura 4: Tracciati cinematici masticatori sul piano assiale.
Traslazione del Condilo Mediotrusivo
Il condilo mediotrusivo, sul lato opposto al movimento laterale, si muove principalmente con una traslazione anteriore e mediale nello spazio tridimensionale. La traslazione è descritta dal seguente vettore:

Dove:
 : Coordinate temporali del condilo mediotrusivo nello spazio cartesiano.
: Coordinate temporali del condilo mediotrusivo nello spazio cartesiano.
Questo tipo di traslazione influenza significativamente i tracciati occlusali, generando variazioni di orientamento durante il ciclo masticatorio.
Descrizione delle misure lineari ed angolari
Rappresentazione scalare dei tracciati condilari
Descrizione delle distanze e delle direzioni
Di seguito sono riportate le distanze calcolate tra i punti rispetto al punto di partenza (punto 1, massima intercuspidazione), considerato punto di riferimento, e le relative direzioni nello spazio, utilizzando le coordinate corrette per gli assi  (antero-posteriore) e
(antero-posteriore) e  (latero-mediale).
(latero-mediale).
Calcolo delle distanze tra i punti
Le coordinate dei punti estrapolate da Geogebra dopo calibrazione, per il condilo laterotrusivo, sono:
- 1L:

- 2L:

- 3L:

- 4L:

- 5L:

- 6L:

- 7L:

- 8L:

Fattore di scala: 
Distanze rispetto a  :
:
 :
:


 :
:


 :
:


 :
:


 :
:


 :
:


 :
:


- ↑ Curtis, D.A. ∙ Sorensen, J.A. Errors incurred in programming a fully adjustable articulator with a pantograph J Prosthet Dent. 1986; 55:427-429
- ↑ Clayton, J.A. ∙ Kotowicz, W.E. ∙ Zahler, J.M. Pantographic tracings of mandibular movements and occlusion J Prosthet Dent. 1971; 75:389-395
- ↑ Shields, J.M. ∙ Clayton, J.A. ∙ Sindledecker, L.D. Using pantographic tracings to detect TMJ and muscle dysfunctions J Prosthet Dent. 1978; 39:80-87
- ↑ Payne, J. Condylar determinants in a patient population: electronic pantograph assessment J Oral Rehabil. 1997; 24:157-163
- ↑ Bennett, N.G. A contribution to the study of the movements of the mandible Proc R Soc Med. 1908; 1:79-98
- ↑ Taylor, T.D. ∙ Bidra, A.S. ∙ Nazarova, E. ... Clinical significance of immediate mandibular lateral translation: A systematic review J Prosthet Dent. 2016; 115:412-418
- ↑
N A Wickwire, C H Gibbs, A P Jacobson, H C Lundeen. Chewing patterns in normal children. Angle Orthod. 1981 Jan;51(1):48-60.


























![{\displaystyle P_{l}(t)=[X_{l}(t),Y_{l}(t),Z_{l}(t),\theta _{l}(t),\phi _{l}(t),\psi _{l}(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0460bad60fdbd2bf924fac810d7383a682d79d9e)