|
|
| (19 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| == Conclusione Integrata: Il Peso dei Condili e il Ruolo dei Tracciati Occlusali == | | == Discussione e Conclusioni == |
|
| |
|
| L’analisi delle traiettorie mandibolari evidenzia una complessa interazione tra movimenti lineari e angolari. Questi movimenti, rilevati nei punti chiave della mandibola, riflettono l'equilibrio tra stabilità e adattabilità dinamica durante la funzione masticatoria. La combinazione dei pesi lineari e angolari offre una visione integrata del contributo relativo di ogni punto articolare, fornendo una base interpretativa robusta per il bilanciamento occlusale.
| | ===Discussione sulla Rototraslazione Condilare e Tracciati Masticatori=== |
|
| |
|
| === Tabella Riassuntiva dei Pesi ===
| | La cinematica mandibolare è il risultato della complessa interazione tra i movimenti dei condili e i tracciati occlusali dei denti, analizzabili tramite i dati geometrici e cinematici. Ogni punto del sistema mandibolare (condili, molari, incisivi) segue traiettorie specifiche che riflettono la dinamica articolare e la relazione occlusale. L'obiettivo di questa discussione è fornire al lettore una comprensione delle correlazioni tra i tracciati condilari e dentali, nonché delle implicazioni cliniche. |
|
| |
|
| {| class="wikitable"
| | '''Relazione tra Condilo Laterotrusivo e Tracciati Occlusali''' |
| |+ **Contributo Lineare e Angolare ai Tracciati Occlusali**
| |
| |-
| |
| ! Area Analizzata !! Distanza (mm) !! Angolo Calcolato (°) !! Reciproco (°) !! Peso Lineare (%) !! Peso Angolare (%) !! Peso Combinato (%)
| |
| |-
| |
| | Condilo Laterotrusivo || 3.16 || 33.57 || 146.43 || 7.8 || 16.7 || 12.3
| |
| |-
| |
| | Molare Laterotrusivo || 9.10 || 72.80 || 107.20 || 22.4 || 12.2 || 17.3
| |
| |-
| |
| | Incisivo || 13.84 || 82.00 || 98.00 || 34.1 || 11.2 || 22.7
| |
| |-
| |
| | Molare Mediotrusivo || 8.99 || 91.33 || 88.67 || 22.1 || 10.1 || 16.1
| |
| |-
| |
| | Condilo Mediotrusivo || 6.25 || 166.00 || 14.00 || 15.4 || 49.8 || 32.6
| |
| |}
| |
|
| |
|
| === Metodo di Calcolo dei Pesi ===
| | Il condilo laterotrusivo rappresenta il lato lavorante e segue un tracciato combinato di rotazione e traslazione laterale. Le distanze e gli angoli calcolati (es. movimento di Bennett, distanza <math>1L_c-7L_c </math> pari a <math>0.898 \, \text{mm}</math>) dimostrano che il condilo cambia direzione durante il movimento masticatorio, invertendo il moto da protrusivo a retrusivo. Questo cambio di direzione corrisponde a una "inversione" dei tracciati occlusali, visibile anche nel molare ipsilaterale e negli incisivi. |
|
| |
|
| Il peso combinato tiene conto di due parametri fondamentali:
| | La figura e la tabella associata dimostrano che i tracciati del condilo laterotrusivo influenzano la distribuzione delle forze occlusali. Ad esempio, il punto estremo del condilo (<math>7L_c</math>) rappresenta un'importante transizione biomeccanica, che può essere utilizzata clinicamente per valutare la stabilità articolare e la simmetria funzionale.Si tenga conto che una pposizione di massima retrusione masticatoria è generata quasi esclusivamente dal muscolo temporale che ha una funzione di chiusura, lateralizzazione e retrusione mandibolare. In sostanza più si masticano cibo du elevata durezza più si sposta posteriormente e la chiusura masticatoria diventa lateroretrusiva.<ref>A Grigoriadis 1, R S Johansson, M Trulsson. Temporal profile and amplitude of human masseter muscle activity is adapted to food properties during individual chewing cycles.J Oral Rehabil. 2014 May;41(5):367-73.doi: 10.1111/joor.12155. Epub 2014 Mar 10. |
|
| |
|
| # Peso Lineare: Determinato dalla distanza percorsa dal punto analizzato rispetto al punto di riferimento (solitamente <math>P_1</math>).
| | </ref><ref>Tomohiro Ishii, Noriyuki Narita, Hiroshi Endo, Masanobu Wakami, Masakazu Okubo, Takeshi Uchida, Ikuo Kantake, Koh Shibutani. Coordinated features in jaw and neck muscle activities induced by chewing of soft and hard gum in healthy subjects. Clin Exp Dent Res. . 2021 Oct;7(5):868-876. doi: 10.1002/cre2.413. Epub 2021 Mar 9. |
| # Peso Angolare: Calcolato come la normalizzazione dell'angolo reciproco rispetto alla somma di tutti i reciproci degli angoli analizzati.
| |
|
| |
|
| I pesi relativi sono ottenuti mediante la seguente procedura:
| | </ref><ref>K Takada, S Miyawaki, M Tatsuta.The effects of food consistency on jaw movement and posterior temporalis and inferior orbicularis oris muscle activities during chewing in children. Arch Oral Biol.1994 Sep;39(9):793-805.doi: 10.1016/0003-9969(94)90009-4. |
|
| |
|
| Peso Lineare Normalizzato:
| | </ref> |
|
| |
|
| <math>P_L = \frac{\text{Distanza del punto}}{\text{Somma di tutte le distanze}}</math>.
| | '''Dinamica dei Molari Ipsilaterali''' |
|
| |
|
| Peso Angolare Normalizzato:
| | I molari ipsilaterali al condilo laterotrusivo seguono un tracciato coerente con il moto condilare, ma la loro traiettoria riflette una maggiore interazione con i punti di contatto occlusali. Come evidenziato nella Tabella 2, i molari mostrano un graduale spostamento laterale con una successiva medializzazione nel punto <math>7L_m</math>, in cui si osserva un angolo di circa <math>73^\circ</math>. |
|
| |
|
| <math>P_A = \frac{\text{Reciproco dell'angolo del punto}}{\text{Somma di tutti i reciproci degli angoli}}</math>.
| | '''Analisi degli Incisivi e la Transizione Occlusale''' |
|
| |
|
| Peso Combinato:
| | Gli incisivi laterotrusivi presentano tracciati che combinano retrusione e lateralizzazione. La distanza <math>1I-7I</math> di <math>5.12 \, \text{mm}</math> con un angolo <math>\theta \approx 85.1^\circ</math> sottolinea una progressiva convergenza verso la massima intercuspidazione. Clinicamente, ciò suggerisce che gli incisivi lavorano come guida durante i movimenti laterali, trasferendo il carico occlusale ai molari mediotrusivi. |
|
| |
|
| <math>P_C = 0.5 \cdot P_L + 0.5 \cdot P_A</math>, per dare, in questo contesto, pari importanza alle componenti lineari e angolari.
| | '''Correlazione con il Condilo Mediotrusivo''' |
|
| |
|
| === Considerazioni Finali ===
| | Il condilo mediotrusivo, che rappresenta il lato bilanciante, segue un tracciato con una combinazione di traslazione mediale e rotazione limitata. La distanza <math>1M_c-7M_c </math> di <math>2.61 \, \text{mm}</math> e un angolo <math>\theta \approx166^\circ </math> evidenziano un movimento più controllato rispetto al condilo laterotrusivo. Questa traiettoria è strettamente correlata con i tracciati del molare mediotrusivo, che seguono una direzione prevalentemente medializzante. |
|
| |
|
| Condilo Laterotrusivo (Lavorante)**
| | La dinamica del molare mediotrusivo, come mostrato nella Tabella 4, rivela un'inversione della direzione al punto <math>6M_m</math>, evidenziando una transizione critica per il bilanciamento delle forze masticatorie. Questo comportamento si collega direttamente al ruolo del condilo mediotrusivo nel controllo della traiettoria occlusale e della stabilità articolare. |
| Con una distanza percorsa relativamente ridotta (3.16 mm) e un angolo di 33.57° (reciproco di 146.43°), il condilo laterotrusivo evidenzia un peso combinato del 12.3%. Questo sottolinea il suo ruolo stabilizzatore durante i movimenti laterali, caratterizzato da un'azione vincolata e guidata sul lato lavorante.
| |
|
| |
|
| Molare Laterotrusivo**
| | '''Implicazioni Cliniche''' |
| La distanza di 9.10 mm e l’angolo di 72.80° (reciproco di 107.20°) assegnano al molare laterotrusivo un peso combinato del 17.3%. Questo riflette la sua rilevanza nel definire i tracciati occlusali laterali, in stretta interazione con il condilo lavorante.
| |
| Incisivo**
| |
| Con la maggiore distanza percorsa (13.84 mm) e un angolo di 82.00° (reciproco di 98.00°), l'incisivo presenta il peso combinato più alto tra i denti (22.7%). Questo conferma il suo ruolo dominante nel bilanciare i movimenti mandibolari anteriori e laterali.
| |
|
| |
|
| Molare Mediotrusivo (Controlaterale)**
| | L'analisi delle correlazioni tra tracciati condilari e occlusali permette di identificare anomalie biomeccaniche e disfunzioni articolari. Ad esempio: |
| Il molare mediotrusivo, con una distanza di 8.99 mm e un angolo di 91.33° (reciproco di 88.67°), ha un peso combinato del 16.1%. Questo dimostra la sua funzione di supporto nella distribuzione delle forze laterali e nella stabilizzazione della traiettoria masticatoria.
| | *Un angolo di Bennett eccessivo (<math>\theta > 20^\circ</math>) potrebbe indicare instabilità articolare o ipermobilità condilare. |
| | *Tracciati irregolari degli incisivi o dei molari possono riflettere asimmetrie muscolari o disfunzioni occlusali. |
|
| |
|
| Condilo Mediotrusivo (Non Lavorante)**
| | Questi dati possono essere utilizzati per ottimizzare i trattamenti protesici e ortodontici, garantendo una migliore distribuzione delle forze occlusali e una riduzione del rischio di disordini temporomandibolari. |
| Nonostante la distanza ridotta (6.25 mm), il condilo mediotrusivo presenta il comportamento angolare più marcato (166.00°, reciproco di 14.00°). Con un peso combinato del 32.6%, enfatizza la sua funzione compensatoria, essenziale per la dinamica orbitale e per mantenere l’equilibrio articolare.
| |
|
| |
|
| L’analisi dei pesi combinati permette di quantificare il contributo specifico dei condili e dei denti alla funzione occlusale, fornendo una visione integrata dei movimenti mandibolari. Questo approccio può essere esteso a modelli clinici per prevedere disfunzioni o pianificare trattamenti personalizzati, migliorando la comprensione biomeccanica della funzione masticatoria.
| | In conclusione la cinematica mandibolare è una rete complessa di rotazioni, traslazioni e interazioni occlusali. L'analisi combinata dei tracciati condilari e dentali offre una comprensione dettagliata della dinamica masticatoria, fornendo strumenti diagnostici essenziali per migliorare la funzione e la stabilità articolare. La costruzione di un modello matematico basato su dati cinematici, come illustrato nelle figure e tabelle, rappresenta un importante passo avanti nella comprensione della biomeccanica mandibolare. |
|
| |
|
| {{Rosso inizio}}qui {{Rosso Fine}}
| |
|
| |
| == Discussioni e conclusioni==
| |
|
| |
| Per rappresentare matematicamente l'interazione tra i condili e il tracciato del punto molare laterotrusivo, incisale, molare mediotrusivo e condilo mediotrusivo, sviluppiamo un formalismo che modelli i movimenti complessi dei condili e l'effetto risultante sul punto molare laterotrusivo.
| |
|
| |
|
| |
| ==Coordinate dei Condili e del Punto Molare==
| |
|
| |
| Consideriamo le coordinate dei condili e del punto molare laterotrusivo nel sistema di riferimento cartesiano tridimensionale:
| |
| * Asse <math>X</math>: orientamento antero-posteriore.
| |
| *Asse <math>Y</math>: lateralità.
| |
| *Asse <math>Z</math>: altezza.
| |
|
| |
| Definiamo:
| |
| *<math>\mathbf{C}_L(0) = (0, 10, 0) </math>: coordinate del condilo laterotrusivo al tempo <math>t = 0</math>.
| |
| *<math>\mathbf{C}_M(0)= (0, -10, 0) </math>: coordinate del condilo mediotrusivo al tempo <math>t = 0</math>.
| |
| *<math>\mathbf{M}_L(0) = (5, 5, -5)</math>: coordinate del punto molare laterotrusivo al tempo <math>t = 0</math>.
| |
|
| |
| ---
| |
|
| |
| ==Rotazione e Traslazione dei CondiliCondilo Laterotrusivo (Lavorante)==
| |
|
| |
| Il movimento del condilo laterotrusivo è descritto da una combinazione di:
| |
| ***Rotazione laterale** con angolo <math>\theta_L</math> rispetto all’asse verticale <math>Z</math>.
| |
| ***Traslazione retrusiva** lungo l'asse <math>X</math>, rappresentata da <math>\mathbf{d}_L </math>.
| |
| '''Rotaizone e traslazione dei condili'''
| |
|
| |
| '''Condilo laterotrusivo (lavorante)'''
| |
|
| |
| Se il moto è piano e la rotazione avviene attorno a un punto <math>\mathbf{P}</math> che non coincide con l'origine, la posizione del condilo laterotrusivo al tempo <math>t</math> è data da:
| |
|
| |
|
| |
| <math>
| |
| \mathbf{C}_L(t) = \mathbf{R}_Z(\theta_L) \cdot (\mathbf{C}_L(0) - \mathbf{P}) + \mathbf{P} + \mathbf{d}_L
| |
| </math>
| |
|
| |
| Dove:
| |
| *<math>\mathbf{R}_Z(\theta_L)</math> è la matrice di rotazione attorno all’asse <math>Z</math>, definita come:
| |
| <math>
| |
| \mathbf{R}_Z(\theta_L) =
| |
| \begin{pmatrix}
| |
| \cos(\theta_L) & -\sin(\theta_L) & 0 \\
| |
| \sin(\theta_L) & \cos(\theta_L) & 0 \\
| |
| 0 & 0 & 1
| |
| \end{pmatrix}
| |
| </math>
| |
|
| |
|
| |
| <math>\mathbf{P}</math> è il punto attorno al quale avviene la rotazione (ad esempio l'origine)
| |
|
| |
|
| |
| <math>\mathbf{d}_L = (-d_L, 0, 0)</math> rappresenta la traslazione retrusiva lungo l'asse <math>X</math>.
| |
|
| |
|
| |
| '''Condilo Mediotrusivo (Non Lavorante)'''
| |
|
| |
| Il condilo mediotrusivo segue un movimento orbitante più complesso, che combina una rotazione con angolo <math>\theta_M</math>.
| |
|
| |
| Se il moto è spaziale, si utilizza la 'formula di Rodrigues'. La posizione del condilo mediotrusivo al tempo <math>t</math> è data da:
| |
|
| |
| <math>
| |
| \mathbf{C}_M(t) = \mathbf{R} \cdot \mathbf{C}_M(0) + \mathbf{d}_M
| |
| </math>
| |
|
| |
| '''Formula di Rodrigues'''
| |
|
| |
| Se la rotazione avviene nello spazio tridimensionale attorno a un asse arbitrario, la formula di Rodrigues si applica come segue:
| |
|
| |
| <math>
| |
| \mathbf{v}_{rot} = \mathbf{v} \cos(\theta) + (\mathbf{k} \times \mathbf{v}) \sin(\theta) + \mathbf{k} (\mathbf{k} \cdot \mathbf{v})(1 - \cos(\theta))
| |
| </math>
| |
|
| |
| Dove:
| |
| *<math>\mathbf{v}</math> è il vettore da ruotare.
| |
| *<math>\mathbf{k}</math> è il versore dell’asse attorno al quale avviene la rotazione.
| |
| *<math>\theta</math> è l’angolo di rotazione.
| |
| '''Applicazione'''
| |
|
| |
| Nel nostro caso, per un moto spaziale:
| |
| *<math>\mathbf{k} = (0, 0, 1)</math> per una rotazione attorno all’asse <math>Z</math>.
| |
| *<math>\mathbf{v} = \mathbf{C}_M(0) - \mathbf{P}</math>, con <math>\mathbf{P}</math> punto di riferimento.
| |
| *La traslazione <math>\mathbf{d}_M </math> descrive il movimento orbitante e mediale.
| |
|
| |
|
| |
| '''Conclusione'''
| |
|
| |
| La descrizione del movimento dei condili deve essere adattata al contesto:
| |
| *Moto piano: Utilizzare la formula per rotazioni attorno a un punto non coincidente con l'origine.
| |
| * Moto spaziale: Adottare la formula di Rodrigues per rotazioni tridimensionali attorno a un asse arbitrario.
| |
|
| |
| Entrambi i metodi garantiscono una rappresentazione accurata dei movimenti combinati di rotazione e traslazione.
| |
|
| |
|
| |
| ===Tracciato del Punto Molarare Laterotrusivo===
| |
|
| |
| Il tracciato del punto molare laterotrusivo è influenzato sia dalla rotazione retrusiva del condilo laterotrusivo sia dal tragitto orbitante del condilo mediotrusivo. La posizione risultante del punto molare laterotrusivo è:
| |
|
| |
| <math>
| |
| \mathbf{M}_L(t) = \mathbf{M}_L(0) + R(\theta_L) \cdot \mathbf{M}_L(0) + \alpha \cdot \mathbf{C}_L(t) + \beta \cdot \mathbf{C}_M(t)
| |
| </math>
| |
|
| |
| dove:
| |
| * <math>R(\theta_L)</math> rappresenta la rotazione laterale del condilo laterotrusivo,
| |
| *<math>\alpha</math> e <math>\beta</math> sono coefficienti di influenza dei movimenti dei condili.
| |
|
| |
|
| |
| '''Formalizzazione della Componente Lateroretrusiva'''
| |
|
| |
| Per descrivere la componente lateroretrusiva, consideriamo l’effetto orbitante del condilo mediotrusivo come una elemento vettoriale aggiuntiva nel movimento del punto molare laterotrusivo:
| |
|
| |
| <math>
| |
| \mathbf{M}_{L,\text{ret}}(t)=\beta \cdot \mathbf{C}_M(t) + (-d_L, 0, -5)
| |
| </math>
| |
|
| |
| dove <math>\mathbf{M}_{L,\text{ret}}(t)</math> rappresenta la componente lateroretrusiva aggiornata, considerando la posizione inferiore del punto molare rispetto ai condili.
| |
|
| |
| Questa versione riveduta riflette la disposizione modificata:
| |
|
| |
| 1. I condili sono ora allineati lungo l'asse <math>Y</math>.
| |
|
| |
| 2. Il punto molare laterotrusivo si trova in una posizione più bassa sull'asse <math>Z</math>, rappresentando una configurazione spaziale in sintonia con la nuova disposizione.
| |
|
| |
| Estendiamo ora il formalismo matematico per includere il comportamento del punto incisale e del punto molare mediotrusivo, completando così la descrizione della dinamica tra i condili e i punti di contatto chiave della mandibola.
| |
|
| |
| ===Tracciato del Punto Incisale===
| |
|
| |
| Il punto incisale segue una traiettoria influenzata dalla combinazione dei movimenti di entrambi i condili, ma il suo spostamento è principalmente una funzione del **movimento globale della mandibola**. Questo tracciato può essere modellato considerando la somma delle componenti laterali e retrusive trasmesse dai condili, con pesi che riflettono la loro influenza sul movimento anteriore della mandibola.
| |
|
| |
| Definiamo il punto incisale come:
| |
|
| |
| <math>
| |
| \mathbf{I}(t) = (x_{I}(t), y_{I}(t), z_{I}(t))
| |
| </math>
| |
|
| |
| La posizione <math>\mathbf{I}(t)</math> è data da:
| |
|
| |
| <math>
| |
| \mathbf{I}(t) = \mathbf{I}(0) + \gamma \cdot R(\theta_L) \cdot \mathbf{C}_L(t) + \delta \cdot R(\theta_M) \cdot \mathbf{C}_M(t)
| |
| </math>
| |
| dove:
| |
| *<math>\gamma</math> e <math>\delta</math> sono coefficienti che riflettono l'influenza proporzionale dei condili sul tracciato incisale,
| |
| *<math>R(\theta_L)</math> e <math>R(\theta_M)</math> rappresentano le rotazioni dei condili laterotrusivo e mediotrusivo, rispettivamente, intorno all'asse verticale <math>Z</math>.
| |
|
| |
| ===Tracciato del Punto Molarare Mediotrusivo===
| |
|
| |
| Analogamente al punto molare laterotrusivo, il punto molare mediotrusivo (<math>\mathbf{M}_M</math>) è influenzato dai movimenti combinati dei due condili, ma con una maggiore influenza del condilo mediotrusivo. Definiamo:
| |
|
| |
| <math>
| |
| \mathbf{M}_M(t) = (x_{m_M}(t), y_{m_M}(t), z_{m_M}(t))
| |
| </math>
| |
|
| |
| Il tracciato di <math>\mathbf{M}_M(t)</math> può essere modellato come:
| |
|
| |
| <math>
| |
| \mathbf{M}_M(t) = \mathbf{M}_M(0) + \beta' \cdot R(\theta_L) \cdot \mathbf{C}_L(t) + \alpha' \cdot R(\theta_M) \cdot \mathbf{C}_M(t)
| |
| </math>
| |
|
| |
| dove:
| |
| *<math>\beta'</math> e <math>\alpha'</math> sono coefficienti che indicano il contributo proporzionale dei movimenti dei condili sul punto molare mediotrusivo,
| |
| *<math>R(\theta_L)</math> e <math>R(\theta_M)</math> descrivono le matrici di rotazione dei condili laterotrusivo e mediotrusivo intorno all'asse <math>Z</math>.
| |
|
| |
| ===Formalizzazione dei Tracciati e Delle Componenti Lateroretrusive===
| |
|
| |
| Per completare la rappresentazione della componente lateroretrusiva sui punti incisale e molari, è essenziale considerare la risultante delle **forze vettoriali** generate dai movimenti dei condili.
| |
|
| |
| Componente Lateroretrusiva del Punto Incisale
| |
|
| |
| <math>
| |
| \mathbf{I}_{\text{ret}}(t) = \delta \cdot \mathbf{C}_M(t) + (-d_I, 0, -5)
| |
| </math>
| |
|
| |
| dove <math>\mathbf{I}_{\text{ret}}(t)</math> rappresenta la traiettoria lateroretrusiva del punto incisale, considerando la componente di retrazione e la posizione inferiore dell'incisale rispetto ai condili sull'asse <math>Z</math>.
| |
| ==Cnclusioni==
| |
| ===Anomalia dell'Asse Cerniera Verticale Z===
| |
|
| |
| Nel campo odontoiatrico, l'asse verticale <math>Z</math> è generalmente considerato un punto di riferimento assoluto poiché determina la 'distanza intercondilare' tra i condili. Tale asse verticale è concepito come un asse cerniera stabile e statico, intorno al quale dovrebbe idealmente avvenire la rotazione laterotrusiva del condilo lavorante. Questa assunzione semplifica la modellizzazione dei movimenti mandibolari, rendendola più prevedibile.
| |
|
| |
| Tuttavia, nel nostro modello emerge una 'anomalia': la retrusione del condilo laterotrusivo non è unicamente influenzata dall’asse verticale <math>Z</math> come asse cerniera indipendente. In realtà, essa dipende anche dalla 'componente orbitante del condilo mediotrusivo', il che implica che i movimenti di entrambi i condili influiscono sul tracciato del punto molare laterotrusivo, del punto incisale e del molare mediotrusivo.
| |
|
| |
| Questo fenomeno rivela che l’asse verticale <math>Z</math> non è in realtà un asse cerniera assoluto e statico, ma piuttosto parte di una dinamica complessa in cui i condili interagiscono reciprocamente. Se si volesse mantenere l'asse <math>Z</math> come un vero asse cerniera stabile, sarebbe necessario ipotizzare che la rotazione laterotrusiva avvenga intorno a un 'centro di rotazione fisso e immutabile'.
| |
|
| |
| Di conseguenza, il formalismo matematico dovrebbe essere modificato come segue:
| |
|
| |
| 1. L'asse <math>Z</math> sarebbe trattato come un 'asse fisso di rotazione' per il condilo laterotrusivo, eliminando le componenti variabili associate alla traslazione retrusiva e all’influenza del condilo mediotrusivo.
| |
|
| |
| 2. Le relazioni cinematiche dovrebbero essere semplificate, assumendo che <math>R(\theta_L)</math> rappresenti una rotazione pura e invariante rispetto a un centro o asse fisso su <math>Z</math>, senza interazioni orbitali.
| |
|
| |
| Tale formalizzazione permetterebbe una descrizione semplificata e statica dei movimenti mandibolari, ma non terrebbe conto della complessità delle interazioni condilari effettive, come abbiamo osservato nel nostro modello fisiologico.
| |
|
| |
| A questo punto la faccenda sembrerebbe contorta ed incomprensibile rimanendo la solita domanda Amletica:
| |
| [[File:Question 2.jpg|left|100x100px]]
| |
| ---- | | ---- |
| ==Appendice== | | ===Discussione sul 'Residuo' dei vettori-conica=== |
| ==Conclusioni su 'Distanze e Direzioni'==
| | La costruzione delle coniche a 5 punti ha permesso di modellare con precisione i tracciati sul Molare laterotrusivo, Incisivo e Molare mediotrusivo. L'uso della 'Conica Unificata' ha offerto una visione globale, ma per una maggiore precisione, le 'coniche specifiche' risultano più adatte per localizzare punti chiave come il punto <math>7L_c </math>. |
| '''Condilo Laterotrusivo (Lavorante)''' | |
| L'analisi cinematica del condilo laterotrusivo evidenzia una traiettoria articolare risultante da una combinazione di movimenti rotatori e traslatori. La traiettoria comprende componenti antero-posteriore e latero-mediale, influenzate dall'interazione con il condilo mediotrusivo. Questo comportamento tridimensionale è essenziale per l'equilibrio funzionale mandibolare, poiché determina la traiettoria e la stabilità dei contatti occlusali durante il ciclo masticatorio. Dal punto di vista clinico, la comprensione dettagliata di queste dinamiche può aiutare a diagnosticare e trattare disfunzioni temporomandibolari (TMD) e asimmetrie mandibolari.
| |
|
| |
|
| '''Molare Laterotrusivo''' | | '''Vettore molare laterotrusivo ipsilaterale''' |
| Il molare laterotrusivo mostra spostamenti lineari di circa 9.1 mm rispetto al punto di massima intercuspidazione, con un angolo calcolato di 73.32°. Questi movimenti riflettono forze e vincoli strutturali imposti dalla morfologia condilare e dall'interazione con il condilo mediotrusivo, influenzando la traiettoria del molare durante la funzione masticatoria. Questo tipo di analisi contribuisce a una comprensione più profonda dei movimenti mandibolari e supporta valutazioni cliniche utili per pianificare interventi riabilitativi.
| |
|
| |
|
| '''Incisivo''' | | Il molare 'laterotrusivo ipsilaterale' mostra un comportamento quasi coincidente con il passaggio della conica. Questo fenomeno si spiega con la 'relazione diretta tra il condilo laterotrusivo e il molare ipsilaterale', poiché la 'rotazione del condilo laterotrusivo' attorno all'asse verticale produce una traiettoria ellittica regolare e la traslazione del condilo laterotrusivo lungo una traiettoria definita genera variazioni che rimangono vincolate alla conica. Matematicamente, considerando la conica com<math>Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0</math> |
| Il movimento dell'incisivo lavorante mostra variazioni di spostamento lineare fino a 13.84 mm. L'angolo tra i segmenti definiti è stato calcolato pari a 85.09°, indicando una significativa mobilità laterale. Questo comportamento riflette un'ampia capacità di adattamento dei muscoli e dei tessuti circostanti per mantenere stabilità e precisione durante la funzione masticatoria. L'analisi quantitativa degli spostamenti lineari e angolari contribuisce alla diagnosi di disfunzioni articolari e alla pianificazione di trattamenti personalizzati.
| |
| | |
| '''Molare Mediotrusivo (Controlaterale)''' | |
| Il molare controlaterale evidenzia una distanza lineare di 8.99 mm e un angolo di circa 91.33°, suggerendo un movimento quasi perpendicolare rispetto ai segmenti di riferimento. Questo movimento garantisce stabilità laterale e un bilanciamento funzionale durante i movimenti masticatori laterali, contribuendo a un'efficace distribuzione delle forze sul lato mediotrusivo. L'analisi matematica di angoli e distanze supporta la diagnosi di disfunzioni articolari e fornisce una base per pianificazioni terapeutiche orientate alla stabilizzazione del sistema masticatorio.
| |
| | |
| '''Condilo Mediotrusivo (Non Lavorante)'''
| |
| Il condilo mediotrusivo segue una traiettoria complessa, caratterizzata da un movimento orbitante che combina spostamenti mediali e anteriori. L'angolo calcolato tra i punti analizzati è risultato pari a 13.57° (Angolo di Bennett). Questo valore riflette un adattamento dinamico durante i movimenti mandibolari laterali, con variazioni angolari che suggeriscono forze anomale o alterazioni potenzialmente indicative di disfunzioni articolari. Queste informazioni sono essenziali per individuare asimmetrie funzionali e migliorare la gestione dei disturbi temporomandibolari.
| |
| | |
| ==Calcolo del Tracciato del Punto Molare Laterotrusivo==
| |
| | |
| ===Coordinate dei Condili e del Punto Molare===
| |
| Consideriamo le coordinate aggiornate per rappresentare i movimenti articolari:
| |
| *<math>\mathbf{C}_L(0) = (63.2,-59.7)</math>: coordinate del condilo laterotrusivo al tempo <math>t = 0</math>.
| |
| *<math>\mathbf{C}_M(0) = (530.6,-61.8)</math>: coordinate del condilo mediotrusivo al tempo <math>t = 0</math>.
| |
| *<math>\mathbf{M}_L(0) = (185.2,-392.7)</math>: coordinate del punto molare laterotrusivo al tempo <math>t = 0</math>.
| |
| | |
| ----
| |
| ===Calcolo del Tracciato del Punto Molare Laterotrusivo===
| |
|
| |
|
| Il tracciato del punto molare laterotrusivo è stato calcolato utilizzando un modello geometrico basato su un'ellisse che rappresenta il movimento ideale del molare, influenzato dai condili laterotrusivo e mediotrusivo. Questo modello tiene conto delle componenti lineari e angolari delle rototraslazioni dei condili, considerando un piano assiale bidimensionale (<math>x, y</math>). È importante sottolineare che le coordinate fornite da GeoGebra sono considerate con assi scambiati rispetto alla convenzione medica, ma ciò non altera i risultati matematici, solo l'interpretazione.
| | e il vettore posizione del molare laterotrusivo come <math>\mathbf{r}_{L_m}(t) = (x_{L_m}(t), y_{L_m}(t))</math>il discostarsi del vettore è determinato dal residuo: |
|
| |
|
| ====Coordinate iniziali====
| | <math>R_{L_m} = A(x_{L_m})^2 + Bx_{L_m}y_{L_m} + C(y_{L_m})^2 + Dx_{L_m} + Ey_{L_m} + F</math> |
| *<math>\mathbf{C}_L(0) = (63.2, -59.7)</math>: condilo laterotrusivo al tempo <math>t = 0</math>.
| |
| *<math>\mathbf{C}_M(0) = (530.6, -61.8)</math>: condilo mediotrusivo al tempo <math>t = 0</math>.
| |
| *<math>\mathbf{M}_L(0) = (185.2, -392.7)</math>: punto molare laterotrusivo al tempo <math>t = 0</math>.
| |
|
| |
|
| ====Modello geometrico basato sull'ellisse====
| | Essendo <math>R_{L_m} \approx 0</math>, il vettore segue quasi perfettamente il passaggio della conica. |
| Per rappresentare la traiettoria del punto molare, è stata costruita un'ellisse con:
| |
| ***Centro**: punto medio tra i condili laterotrusivo e mediotrusivo:
| |
| <math>\text{Centro} = \left( \frac{63.2 + 530.6}{2}, \frac{-59.7 + -61.8}{2} \right) = (296.9, -60.75)</math>
| |
| * **Semi-asse maggiore (<math>a</math>)**: distanza dal centro al condilo laterotrusivo (<math>C_L</math>):
| |
| <math>a = \sqrt{(296.9 - 63.2)^2 + (-60.75 - -59.7)^2} \approx 233.7.</math> | |
| ***Semi-asse minore (<math>b</math>)**: assunto pari a metà del semi-asse maggiore:
| |
| <math>b = \frac{a}{2} \approx 116.85 </math>
| |
|
| |
|
| L'equazione dell'ellisse è quindi:
| | '''Vettore molare controlaterale (mediotrusivo)''' |
| <math>\frac{(X - 296.9)^2}{233.7^2} + \frac{(Y + 60.75)^2}{116.85^2} = 1</math>
| |
|
| |
|
| ====Determinazione del punto <math>M_7</math>====
| | Il molare 'controlaterale' (mediotrusivo) si discosta maggiormente dalla conica. Questo fenomeno si verifica perché il condilo compie un movimento prevalentemente traslatorio con una componente minima di rotazione e la traiettoria del molare controlaterale risente delle variazioni angolari complesse del condilo mediotrusivo, generando deviazioni dal piano della conica. Geometricamente, la traiettoria del molare mediotrusivo non segue perfettamente la conica a causa delle componenti traslazionali che deviano il tracciato rispetto alla curva ellittica ideale. |
| Il punto <math>M_7</math>, rappresentante la posizione del molare laterotrusivo al tempo <math>t = 7</math>, deve soddisfare due condizioni:
| |
|
| |
|
| # Trovarsi sull'ellisse, rispettando l'equazione:
| | Matematicamente, il residuo per il molare mediotrusivo dato da<math>R_{M_m} = A(x_{M_m})^2 + Bx_{M_m}y_{M_m} + C(y_{M_m})^2 + Dx_{M_m} + Ey_{M_m} + F</math> |
| # <math>\frac{(X - 296.9)^2}{233.7^2} + \frac{(Y + 60.75)^2}{116.85^2} = 1 </math>
| |
| # Essere il più vicino possibile al punto reale osservato:
| |
| # <math>M_7 \approx (129.34, -380.40).</math>
| |
|
| |
|
| Attraverso un algoritmo iterativo, il punto <math>M_7</math> è stato calcolato come:
| | con<math>|R_{M_m}| > |R_{L_m}|</math>dimostra un maggiore scostamento rispetto alla conica. |
|
| |
|
| <math>M_7 = (129.34, -380.40).</math>
| | '''Vettore incisale''' |
|
| |
|
| ==== Conclusioni====
| | Il vettore incisale si colloca in una posizione intermedia rispetto ai molari ipsilaterali e controlaterali. Questo perchè gli 'incisivi' sono influenzati dalla combinazione dei movimenti del condilo laterotrusivo e del condilo mediotrusivo. La traiettoria degli incisivi segue una curva regolare ma leggermente deviata rispetto alla conica. Matematicamente,il residuo per il vettore incisale è dato da<math>R_I = A(x_I)^2 + Bx_Iy_I + C(y_I)^2 + Dx_I + Ey_I + F</math>con<math>|R_{L_m}| < |R_I| < |R_{M_m}|</math>dimostrando che il vettore incisale si discosta più del molare ipsilaterale ma meno del molare controlaterale. |
| L'ellisse definisce una traiettoria ideale per il molare laterotrusivo, influenzata dalle rototraslazioni dei condili laterotrusivo e mediotrusivo. Il punto <math>M_7</math> calcolato è coerente con i dati reali, mostrando come i movimenti condilari determinino direttamente il tracciato occlusale del molare. Questo approccio geometrico semplificato è utile per analizzare e correlare i movimenti articolari mandibolari ai tracciati dentali.
| | {{q2|C'è qualcosa che ancora non va?|......si certo è la nostra abitudine di osservare il sistema come una cinematica di un punto mentre dietro il fenomeno della magia della sfera condilare si celano altre verità}} |
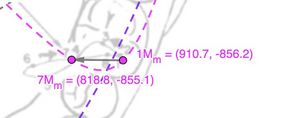
| | [[File:Residui Conica 1.jpg|thumb]]In conclusione, se osserviamo i tracciati rilevati dal Replicator sul molare mediotrusivo possiamo verificare come il vettore con direzione <math>7M_m</math> che sostanzialmente genera il solco mediotrusivo tra la cuspide centrale e distale del molare si discosta dalla ellisse generata dalla conica a 5 punti perchè è stato trascurata l'influenza che genera sul sistema cinematico la sfera condilare. Argomento che tratteremo al prossimo capitolo. |
Discussione e Conclusioni
Discussione sulla Rototraslazione Condilare e Tracciati Masticatori
La cinematica mandibolare è il risultato della complessa interazione tra i movimenti dei condili e i tracciati occlusali dei denti, analizzabili tramite i dati geometrici e cinematici. Ogni punto del sistema mandibolare (condili, molari, incisivi) segue traiettorie specifiche che riflettono la dinamica articolare e la relazione occlusale. L'obiettivo di questa discussione è fornire al lettore una comprensione delle correlazioni tra i tracciati condilari e dentali, nonché delle implicazioni cliniche.
Relazione tra Condilo Laterotrusivo e Tracciati Occlusali
Il condilo laterotrusivo rappresenta il lato lavorante e segue un tracciato combinato di rotazione e traslazione laterale. Le distanze e gli angoli calcolati (es. movimento di Bennett, distanza  pari a
pari a  ) dimostrano che il condilo cambia direzione durante il movimento masticatorio, invertendo il moto da protrusivo a retrusivo. Questo cambio di direzione corrisponde a una "inversione" dei tracciati occlusali, visibile anche nel molare ipsilaterale e negli incisivi.
) dimostrano che il condilo cambia direzione durante il movimento masticatorio, invertendo il moto da protrusivo a retrusivo. Questo cambio di direzione corrisponde a una "inversione" dei tracciati occlusali, visibile anche nel molare ipsilaterale e negli incisivi.
La figura e la tabella associata dimostrano che i tracciati del condilo laterotrusivo influenzano la distribuzione delle forze occlusali. Ad esempio, il punto estremo del condilo ( ) rappresenta un'importante transizione biomeccanica, che può essere utilizzata clinicamente per valutare la stabilità articolare e la simmetria funzionale.Si tenga conto che una pposizione di massima retrusione masticatoria è generata quasi esclusivamente dal muscolo temporale che ha una funzione di chiusura, lateralizzazione e retrusione mandibolare. In sostanza più si masticano cibo du elevata durezza più si sposta posteriormente e la chiusura masticatoria diventa lateroretrusiva.[1][2][3]
) rappresenta un'importante transizione biomeccanica, che può essere utilizzata clinicamente per valutare la stabilità articolare e la simmetria funzionale.Si tenga conto che una pposizione di massima retrusione masticatoria è generata quasi esclusivamente dal muscolo temporale che ha una funzione di chiusura, lateralizzazione e retrusione mandibolare. In sostanza più si masticano cibo du elevata durezza più si sposta posteriormente e la chiusura masticatoria diventa lateroretrusiva.[1][2][3]
Dinamica dei Molari Ipsilaterali
I molari ipsilaterali al condilo laterotrusivo seguono un tracciato coerente con il moto condilare, ma la loro traiettoria riflette una maggiore interazione con i punti di contatto occlusali. Come evidenziato nella Tabella 2, i molari mostrano un graduale spostamento laterale con una successiva medializzazione nel punto  , in cui si osserva un angolo di circa
, in cui si osserva un angolo di circa  .
.
Analisi degli Incisivi e la Transizione Occlusale
Gli incisivi laterotrusivi presentano tracciati che combinano retrusione e lateralizzazione. La distanza  di
di  con un angolo
con un angolo  sottolinea una progressiva convergenza verso la massima intercuspidazione. Clinicamente, ciò suggerisce che gli incisivi lavorano come guida durante i movimenti laterali, trasferendo il carico occlusale ai molari mediotrusivi.
sottolinea una progressiva convergenza verso la massima intercuspidazione. Clinicamente, ciò suggerisce che gli incisivi lavorano come guida durante i movimenti laterali, trasferendo il carico occlusale ai molari mediotrusivi.
Correlazione con il Condilo Mediotrusivo
Il condilo mediotrusivo, che rappresenta il lato bilanciante, segue un tracciato con una combinazione di traslazione mediale e rotazione limitata. La distanza  di
di  e un angolo
e un angolo  evidenziano un movimento più controllato rispetto al condilo laterotrusivo. Questa traiettoria è strettamente correlata con i tracciati del molare mediotrusivo, che seguono una direzione prevalentemente medializzante.
evidenziano un movimento più controllato rispetto al condilo laterotrusivo. Questa traiettoria è strettamente correlata con i tracciati del molare mediotrusivo, che seguono una direzione prevalentemente medializzante.
La dinamica del molare mediotrusivo, come mostrato nella Tabella 4, rivela un'inversione della direzione al punto  , evidenziando una transizione critica per il bilanciamento delle forze masticatorie. Questo comportamento si collega direttamente al ruolo del condilo mediotrusivo nel controllo della traiettoria occlusale e della stabilità articolare.
, evidenziando una transizione critica per il bilanciamento delle forze masticatorie. Questo comportamento si collega direttamente al ruolo del condilo mediotrusivo nel controllo della traiettoria occlusale e della stabilità articolare.
Implicazioni Cliniche
L'analisi delle correlazioni tra tracciati condilari e occlusali permette di identificare anomalie biomeccaniche e disfunzioni articolari. Ad esempio:
- Un angolo di Bennett eccessivo (
 ) potrebbe indicare instabilità articolare o ipermobilità condilare.
) potrebbe indicare instabilità articolare o ipermobilità condilare.
- Tracciati irregolari degli incisivi o dei molari possono riflettere asimmetrie muscolari o disfunzioni occlusali.
Questi dati possono essere utilizzati per ottimizzare i trattamenti protesici e ortodontici, garantendo una migliore distribuzione delle forze occlusali e una riduzione del rischio di disordini temporomandibolari.
In conclusione la cinematica mandibolare è una rete complessa di rotazioni, traslazioni e interazioni occlusali. L'analisi combinata dei tracciati condilari e dentali offre una comprensione dettagliata della dinamica masticatoria, fornendo strumenti diagnostici essenziali per migliorare la funzione e la stabilità articolare. La costruzione di un modello matematico basato su dati cinematici, come illustrato nelle figure e tabelle, rappresenta un importante passo avanti nella comprensione della biomeccanica mandibolare.
Discussione sul 'Residuo' dei vettori-conica
La costruzione delle coniche a 5 punti ha permesso di modellare con precisione i tracciati sul Molare laterotrusivo, Incisivo e Molare mediotrusivo. L'uso della 'Conica Unificata' ha offerto una visione globale, ma per una maggiore precisione, le 'coniche specifiche' risultano più adatte per localizzare punti chiave come il punto  .
.
Vettore molare laterotrusivo ipsilaterale
Il molare 'laterotrusivo ipsilaterale' mostra un comportamento quasi coincidente con il passaggio della conica. Questo fenomeno si spiega con la 'relazione diretta tra il condilo laterotrusivo e il molare ipsilaterale', poiché la 'rotazione del condilo laterotrusivo' attorno all'asse verticale produce una traiettoria ellittica regolare e la traslazione del condilo laterotrusivo lungo una traiettoria definita genera variazioni che rimangono vincolate alla conica. Matematicamente, considerando la conica com
e il vettore posizione del molare laterotrusivo come  il discostarsi del vettore è determinato dal residuo:
il discostarsi del vettore è determinato dal residuo:

Essendo  , il vettore segue quasi perfettamente il passaggio della conica.
, il vettore segue quasi perfettamente il passaggio della conica.
Vettore molare controlaterale (mediotrusivo)
Il molare 'controlaterale' (mediotrusivo) si discosta maggiormente dalla conica. Questo fenomeno si verifica perché il condilo compie un movimento prevalentemente traslatorio con una componente minima di rotazione e la traiettoria del molare controlaterale risente delle variazioni angolari complesse del condilo mediotrusivo, generando deviazioni dal piano della conica. Geometricamente, la traiettoria del molare mediotrusivo non segue perfettamente la conica a causa delle componenti traslazionali che deviano il tracciato rispetto alla curva ellittica ideale.
Matematicamente, il residuo per il molare mediotrusivo dato da
con dimostra un maggiore scostamento rispetto alla conica.
dimostra un maggiore scostamento rispetto alla conica.
Vettore incisale
Il vettore incisale si colloca in una posizione intermedia rispetto ai molari ipsilaterali e controlaterali. Questo perchè gli 'incisivi' sono influenzati dalla combinazione dei movimenti del condilo laterotrusivo e del condilo mediotrusivo. La traiettoria degli incisivi segue una curva regolare ma leggermente deviata rispetto alla conica. Matematicamente,il residuo per il vettore incisale è dato da con
con dimostrando che il vettore incisale si discosta più del molare ipsilaterale ma meno del molare controlaterale.
dimostrando che il vettore incisale si discosta più del molare ipsilaterale ma meno del molare controlaterale.
«C'è qualcosa che ancora non va?»
(......si certo è la nostra abitudine di osservare il sistema come una cinematica di un punto mentre dietro il fenomeno della magia della sfera condilare si celano altre verità)
In conclusione, se osserviamo i tracciati rilevati dal Replicator sul molare mediotrusivo possiamo verificare come il vettore con direzione  che sostanzialmente genera il solco mediotrusivo tra la cuspide centrale e distale del molare si discosta dalla ellisse generata dalla conica a 5 punti perchè è stato trascurata l'influenza che genera sul sistema cinematico la sfera condilare. Argomento che tratteremo al prossimo capitolo.
che sostanzialmente genera il solco mediotrusivo tra la cuspide centrale e distale del molare si discosta dalla ellisse generata dalla conica a 5 punti perchè è stato trascurata l'influenza che genera sul sistema cinematico la sfera condilare. Argomento che tratteremo al prossimo capitolo.
- ↑ A Grigoriadis 1, R S Johansson, M Trulsson. Temporal profile and amplitude of human masseter muscle activity is adapted to food properties during individual chewing cycles.J Oral Rehabil. 2014 May;41(5):367-73.doi: 10.1111/joor.12155. Epub 2014 Mar 10.
- ↑ Tomohiro Ishii, Noriyuki Narita, Hiroshi Endo, Masanobu Wakami, Masakazu Okubo, Takeshi Uchida, Ikuo Kantake, Koh Shibutani. Coordinated features in jaw and neck muscle activities induced by chewing of soft and hard gum in healthy subjects. Clin Exp Dent Res. . 2021 Oct;7(5):868-876. doi: 10.1002/cre2.413. Epub 2021 Mar 9.
- ↑ K Takada, S Miyawaki, M Tatsuta.The effects of food consistency on jaw movement and posterior temporalis and inferior orbicularis oris muscle activities during chewing in children. Arch Oral Biol.1994 Sep;39(9):793-805.doi: 10.1016/0003-9969(94)90009-4.