Difference between revisions of "Store:ACincisivo"
| (18 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<P>'''Incisal'''</P> | |||
Il paragrafo | |||
Il paragrafo descrive un'analisi matematica dei movimenti articolari dell'incisivo sul lato lavorante. Utilizzando le coordinate di tre punti nello spazio 2D <math> 1_ I </math>, <math>7_I</math> e <math>{R_p}^+</math>, vengono calcolate le distanze lineari tra i punti, oltre all'angolo tra i segmenti che collegano questi punti. | |||
<Center> | <Center> | ||
{| | {| class="wikitable" | ||
! colspan="5" | Tabella 3 | ! colspan="5" |Tabella 3 | ||
|- | |- | ||
!Tracciato masticatorio | !Tracciato masticatorio | ||
!Markers | !Markers | ||
!Distanza (mm) | !Distanza (mm) | ||
!Direzione | !Direzione | ||
<math>X</math> | |||
!Direzione dinamica | !Direzione dinamica | ||
<math>Y</math> | |||
|- | |- | ||
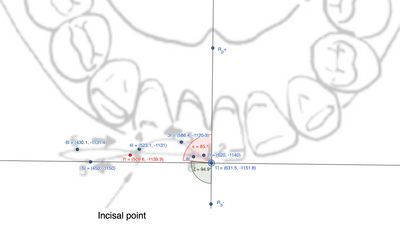
| rowspan="8" |[[File:Figura | | rowspan="8" |[[File:Figura 34finale.jpg|center|400x400px|Figura 3: Rappresentazione delle distanze tra punti dell'incisivo]]'''Figura 7:''' <small>Rappresentazione grafica dei markers rilevati dal 'Replicator'</small> <small>nella masticazione sul lato destro del paziente nell'area inccisale.</small> | ||
| 2 | |2 | ||
| | |0.69 | ||
| | |Retrusiva | ||
|Lateralizzazione | |Lateralizzazione | ||
|- | |- | ||
|3 | |3 | ||
| | |2.30 | ||
| | |Retrusiva | ||
|Lateralizzazione | |Lateralizzazione | ||
|- | |- | ||
|4 | |4 | ||
| | |4.61 | ||
| | |Retrusiva | ||
|Lateralizzazione | |Lateralizzazione | ||
|- | |- | ||
|5 | |5 | ||
| | |7.58 | ||
| | |Protrusivo | ||
|Lateralizzazione | |Lateralizzazione | ||
|- | |- | ||
|6 | |6 | ||
| | |8.54 | ||
| | |Retrusiva | ||
|Inversione | |Inversione | ||
|- | |- | ||
|7* | |7* | ||
| | |5.12 | ||
| | |Retrusiva | ||
|Medializzazione | |Medializzazione | ||
|- | |- | ||
|8 | |8 | ||
| | |1.75 | ||
| | |Retrusiva | ||
|Medializzazione | |Medializzazione | ||
|- | |- | ||
| Line 54: | Line 57: | ||
</Center> | </Center> | ||
Per quanto riguarda i tracciati nell'area dell'incisivo tra il punto <math> | Per quanto riguarda i tracciati nell'area dell'incisivo tra il punto <math>1I</math> e <math>7I</math>, la distanza risulta essere di <math>5.12_{mm}</math> con un angolo approssimativamente pari a <math>85.1^\circ</math>. Per approfondimenti di calcolo, vedi la spiegazione dettagliata qui | ||
{{Tooltip|2=Coordinate dei punti: <math>1I = (631.5, -1151.8)</math>, <math>7I = (509.6, -1139.9)</math>, <math>R_p^+ = (634.3, -912.8)</math>. Vettori: <math>\vec{1I7I} = (-121.9, 11.9)</math>, <math>\vec{1IR_p^+} = (2.8, 239)</math>. Norme: <math>|\vec{1I7I}| = 122.49</math>, <math>|\vec{1IR_p^+}| = 238.95</math>. Prodotto scalare: <math>\vec{1I7I} \cdot \vec{1IR_p^+} = 2502.78</math>. Coseno: <math>\cos(\theta) = \frac{2502.78}{122.49 \cdot 238.95} \approx 0.0855</math>. Angolo: <math>\theta = \arccos(0.0855) \approx 85.1^\circ</math>.}} | |||
{{Tooltip|2=Coordinate dei punti: <math> | |||
---- | |||
Latest revision as of 17:57, 26 December 2024
Incisal
Il paragrafo descrive un'analisi matematica dei movimenti articolari dell'incisivo sul lato lavorante. Utilizzando le coordinate di tre punti nello spazio 2D , e , vengono calcolate le distanze lineari tra i punti, oltre all'angolo tra i segmenti che collegano questi punti.
| Tabella 3 | ||||
|---|---|---|---|---|
| Tracciato masticatorio | Markers | Distanza (mm) | Direzione
|
Direzione dinamica
|
| Figura 7: Rappresentazione grafica dei markers rilevati dal 'Replicator' nella masticazione sul lato destro del paziente nell'area inccisale. | 2 | 0.69 | Retrusiva | Lateralizzazione |
| 3 | 2.30 | Retrusiva | Lateralizzazione | |
| 4 | 4.61 | Retrusiva | Lateralizzazione | |
| 5 | 7.58 | Protrusivo | Lateralizzazione | |
| 6 | 8.54 | Retrusiva | Inversione | |
| 7* | 5.12 | Retrusiva | Medializzazione | |
| 8 | 1.75 | Retrusiva | Medializzazione | |
Per quanto riguarda i tracciati nell'area dell'incisivo tra il punto e , la distanza risulta essere di con un angolo approssimativamente pari a . Per approfondimenti di calcolo, vedi la spiegazione dettagliata qui
![]() Coordinate dei punti: , , . Vettori: , . Norme: , . Prodotto scalare: . Coseno: . Angolo: .
Coordinate dei punti: , , . Vettori: , . Norme: , . Prodotto scalare: . Coseno: . Angolo: .