|
|
| (19 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| ===Molare laterotrusivo===
| | '''Molare Laterotrusivo''' |
| Il testo descrive un'analisi dettagliata dei movimenti articolari del molare ipsilaterale al condilo laterotrusivo (Figura 3 e tabella 2)e coinvolge vari punti nello spazio 2D per calcolare distanze e angoli utilizzando la trigonometria vettoriale. | | |
| | Il testo descrive un'analisi dettagliata dei movimenti articolari del molare ipsilaterale al condilo laterotrusivo (Figura 6 e Tabella 2). L'analisi si basa sul calcolo delle distanze tra punti e degli angoli formati tra i vettori utilizzando la trigonometria vettoriale. |
| | |
| <Center> | | <Center> |
| {| | | {| class="wikitable" |
| ! colspan="5" |Tabella 2 | | ! colspan="5" |Tabella 2 |
| |- | | |- |
| !Tracciato masticatorio | | !Tracciato masticatorio |
| !Markers | | !Markers |
| !Distance | | !Distanza |
| (mm) | | (mm) |
| !Direzione in X | | !Direzione |
| (antero-posteriore)
| | <math>X</math> |
| !Direzione | | !Direzione dinamica |
| dinamica | | <math>Y</math> |
| | |
| (Y-latero-mediale)
| |
| |- | | |- |
| | rowspan="8" |[[File:Angolo molare.jpg|'''Figura 3:''' Rappresentazione delle distanze tra punti nel molare ipsilaterale alla laterotrusione|center|400x400px]]'''Figura 2:''' | | | rowspan="8" |[[File:Figura 3 finale.jpg|center|399x399px|'''Figura 3:''' Rappresentazione delle distanze tra punti nel molare ipsilaterale alla laterotrusione]]'''Figura 6:''' <small>Rappresentazione grafica dei markers rilevati dal 'Replicator' nella masticazione sul lato destro del paziente</small> |
| |2 | | |2 |
| |0.8 | | |0.39 |
| |Indietro | | |Indietro |
| |Lateralizzazione | | |Lateralizzazione |
| |- | | |- |
| |3 | | |3 |
| |5.4 | | |2.18 |
| |Indietro | | |Indietro |
| |Lateralizzazione | | |Lateralizzazione |
| |- | | |- |
| | 4 | | |4 |
| |8.4 | | |3.57 |
| | Indietro | | |Indietro |
| |Lateralizzazione | | |Lateralizzazione |
| |- | | |- |
| |5 | | |5 |
| |13.4 | | |5.68 |
| |Indietro | | |Indietro |
| |Lateralizzazione | | |Lateralizzazione |
| |- | | |- |
| |6 | | |6 |
| |16.0 | | |6.76 |
| |Indietro | | |Indietro |
| |Inversione | | |Inversione |
| |- | | |- |
| | 7* | | |7* |
| |9.1 | | |3.93 |
| |Indietro | | |Indietro |
| |Medializzazione | | |Medializzazione |
| |- | | |- |
| |8 | | |8 |
| |2.7 | | |1.15 |
| |Indietro | | |Indietro |
| |Medializzazione | | |Medializzazione |
| Line 55: |
Line 55: |
| |} | | |} |
| </Center> | | </Center> |
| Il formalismo matematico è lo stesso di quello precedentemente descritto e inserito nella nota informativa {{Tooltip|2=Nel contesto della nostra analisi, abbiamo tre punti nello spazio 2D che ci interessano: Coordinate <math> P1_{m}</math> del punto 1 del molare ipsilaterale al condilo latorotrusivo:<math>(345.2, -844.5) </math> *Coordinate <math>P7_{m}</math> del punto 7 del molare ipsilaterale al condilo latorotrusivo: <math>(255.7, -816) </math> *Coordinate <math>R_p</math> del punto di riferimento del condilo mediotrusivo: <math>(347.7, -682.7)</math> Questi punti rappresentano tre posizioni specifiche all'interno di un sistema articolare che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti <math>P1_{m}</math> e <math>P7_{m}</math>, e il segmento che unisce i punti <math>P1_{m}</math> e <math>R_p</math>. Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio.'''Iter matematico per il calcolo dell'angolo''' L'angolo tra due segmenti può essere calcolato utilizzando la **trigonometria vettoriale** e, in particolare, il **prodotto scalare**. Questo metodo è utile quando vogliamo determinare la relazione angolare tra due movimenti distinti nello spazio. {{Tooltip|'''Definizione dei vettori'''| *Il vettore tra il punto <math>P1_{m}</math> e il punto <math>P7_{m}</math>: <math>\vec{AB} = P7_{m} -P1_{m} = (255.7, -816) - (345.2, -844.5) = (-89.5, 28.5)</math> *Il vettore tra il punto <math>P1_{m}</math> e il punto <math>H3 _{m}</math>: <math>\vec{AC} = \vec{R_p} - \vec{P_1} = (347.7, -682.7) - (345.2, -844.5) = (2.5, 161.8)</math>|2}}
| | |
| Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti: {{Tooltip|'''Prodotto scalare'''|Sostituendo i valori calcolati: <math>\vec{AB} \cdot \vec{AC} = (-89.5) \cdot (2.5) + (28.5) \cdot (161.8) = -223.75 + 4601.3 = 4377.55</math> |2}} Il **prodotto scalare** tra due vettori <math>\vec{AB}</math> e <math>\vec{AC }</math> è dato dalla formula: <math>\vec{AB} \cdot \vec{AC} = AB_x \cdot AC_x + AB_y \cdot AC_y</math>{{Tooltip|'''Calcolo delle norme'''| <math>|\vec{AB}| = \sqrt{AB_x^2 + AB_y^2} = \sqrt{(-89.5)^2 + (28.5)^2} = \sqrt{8010.25 + 812.25} = \sqrt{8822.5} \approx 93.96</math> <math>|\vec{AC}| = \sqrt{AC_x^2 + AC_y^2} = \sqrt{(2.5)^2 + (161.8)^2} = \sqrt{6.25 + 26178.44} = \sqrt{26184.69} \approx 161.78</math>.|2}} Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore {{Tooltip|'''Calcolo dell'angolo'''|<math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}</math> Sostituendo i valori: <math>\cos(\theta) = \frac{4377.55}{93.96 \cdot 161.78} = \frac{4377.55}{15193.68} \approx 0.288</math>|2}} Ora possiamo usare la formula per il coseno dell'angolo tra i due vettori: Infine, l'angolo <math>\theta</math> è calcolato tramite la funzione arcoseno: <math>\theta = \arccos(0.288) \approx 73.32^\circ</math> '''Motivo dell'analisi''' L'obiettivo dell'analisi è determinare l'angolo tra due movimenti all'interno di un sistema articolare, in particolare nell'area di studio della cinematica masticatoria.}} ed il risultato lineare ed angolare è di <math>9.1 </math> mm rispetto al punto <math>7^* </math> ed il coseno dell'angolo è stato calcolato come <math>0.288 </math> , con l'angolo risultante approssimativamente pari a <math>
| | Osservando la figura e la tabella, possiamo estrapolare le distanze e le direzioni dei punti marcati. Nello specifico, la distanza del punto <math>7L_m</math> rispetto al punto iniziale <math>1L_m</math> è stata calcolata come circa <math>3.93 \,_ \text{mm}</math>, con un angolo formato tra i vettori pari a <math>\cong 73 ^\circ</math>.{{Tooltip|2=Definizione dei vettori:<math>\vec{AB} = 7L_m - 1L_m = (255.7, -816.0) - (345.2, -844.5) = (-89.5, 28.5)</math>, <math>\vec{AC} = R_p - 1L_m = (346.6, -727.1) - (345.2, -844.5) = (1.4, 117.4)</math>. Magnitudine di <math>\vec{AB}</math>: <math>|\vec{AB}| = \sqrt{(-89.5)^2 + (28.5)^2} \approx 93.93</math>, magnitudine di <math>\vec{AC}</math>: <math>|\vec{AC}| = \sqrt{(1.4)^2 + (117.4)^2} \approx 117.41</math>. Prodotto scalare: <math>\vec{AB} \cdot \vec{AC} = (-89.5)(1.4) + (28.5)(117.4) = 2928.4</math>, <math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|} = \frac{2928.4}{93.93 \cdot 117.41} \approx 0.292</math>, angolo: <math>\theta = \arccos(0.292) \approx 73.02^\circ</math>}} |
| 73.32^\circ</math>.
| | |
| | |
| | ---- |
Latest revision as of 18:12, 26 December 2024
Molare Laterotrusivo
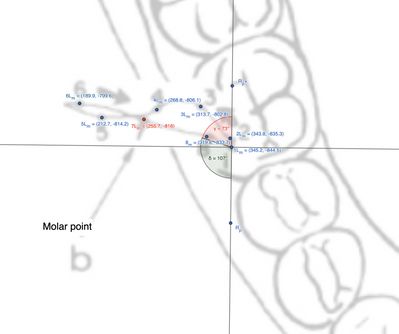
Il testo descrive un'analisi dettagliata dei movimenti articolari del molare ipsilaterale al condilo laterotrusivo (Figura 6 e Tabella 2). L'analisi si basa sul calcolo delle distanze tra punti e degli angoli formati tra i vettori utilizzando la trigonometria vettoriale.
| Tabella 2
|
| Tracciato masticatorio
|
Markers
|
Distanza
(mm)
|
Direzione

|
Direzione dinamica

|
| Figura 6: Rappresentazione grafica dei markers rilevati dal 'Replicator' nella masticazione sul lato destro del paziente
|
2
|
0.39
|
Indietro
|
Lateralizzazione
|
| 3
|
2.18
|
Indietro
|
Lateralizzazione
|
| 4
|
3.57
|
Indietro
|
Lateralizzazione
|
| 5
|
5.68
|
Indietro
|
Lateralizzazione
|
| 6
|
6.76
|
Indietro
|
Inversione
|
| 7*
|
3.93
|
Indietro
|
Medializzazione
|
| 8
|
1.15
|
Indietro
|
Medializzazione
|
|
|
Osservando la figura e la tabella, possiamo estrapolare le distanze e le direzioni dei punti marcati. Nello specifico, la distanza del punto  rispetto al punto iniziale
rispetto al punto iniziale  è stata calcolata come circa
è stata calcolata come circa  , con un angolo formato tra i vettori pari a
, con un angolo formato tra i vettori pari a  .
.  Definizione dei vettori:
Definizione dei vettori: ,
,  . Magnitudine di
. Magnitudine di  :
:  , magnitudine di
, magnitudine di  :
:  . Prodotto scalare:
. Prodotto scalare:  ,
,  , angolo:
, angolo: 
![]() Definizione dei vettori:, . Magnitudine di : , magnitudine di : . Prodotto scalare: , , angolo:
Definizione dei vettori:, . Magnitudine di : , magnitudine di : . Prodotto scalare: , , angolo: