Difference between revisions of "Store:Asse Cerniera verticale parte 1"

Latest revision as of 12:10, 29 December 2024

Introduzione

Nel capitolo precedente, 'Transverse Hinge Axis', abbiamo introdotto la cinematica mandibolare concentrandoci sul piano sagittale. Durante i movimenti di protrusione e retrusione, la mandibola non si muove esclusivamente lungo l'asse $X$ , ma ruota attorno al centro dell'asse $Y$ . Questo movimento condilare si manifesta anteriormente, dove l'incisivo mandibolare segue traiettorie curvilinee inverse, risultato di un complesso moto spaziale generato dalla rototraslazione sugli assi condilari. Lo spazio angolare risultante, noto come 'Spazio libero Interincisivo', è essenziale per consentire movimenti masticatori fluidi e senza ostacoli.

Questo 'Spazio libero Interincisivo' riveste un ruolo cruciale nelle funzioni masticatorie. Tuttavia, strumenti come il Sirognatograph e i sistemi elettromagnetici tradizionali trascurano la componente rotazionale dei movimenti condilari, focalizzandosi principalmente sulle traslazioni. Sebbene ciò possa essere sufficiente per alcune registrazioni, tale approccio è limitato nel cogliere la complessità dei movimenti mandibolari a sei gradi di libertà.

Cinematica Mandibolare a Sei Gradi di Libertà

Il movimento mandibolare avviene in uno spazio tridimensionale e può essere descritto come un complesso moto spaziale. Ogni condilo è associato a tre assi principali:

Asse $Y$ (latero-mediale): Definisce la rotazione attorno all'asse cerniera trasversale ( $_{t}HA$ , transverse Hinge Axis).
**Asse $Z$ (verticale):** Definisce la rotazione sull'asse cerniera verticale ( $_{v}HA$ ).
**Asse $X$ (antero-posteriore): Definisce la rotazione attorno all'asse cerniera orizzontale ( $_{o}HA$ ).

A ciascun asse corrisponde un piano di riferimento anatomico:

Piano sagittale: Mostra il tracciato condilare prodotto dal movimento di rototraslazione dell'asse trasversale ( $_{t}HA$ ).
Piano coronale: Associato all'asse orizzontale ( $_{o}HA$ ).
Piano assiale: Legato al movimento generato attorno all'asse verticale ( $_{v}HA$ , noto anche come asse cerniera verticale).

Va evidenziato che un piano non è generato da un asse; un asse può al massimo essere contenuto in un piano o rappresentare una direzione. Più precisamente, il movimento di un asse genera una 'superficie rigata', che descrive le traiettorie spaziali risultanti.

Asse cerniera verticale

Ci concentreremo sull’asse cerniera verticale ( $_{v}HA$ ) per la sua rilevanza nei sistemi di registrazione cinematici come pantografi, elegnatografi e assiografi. Tuttavia, è necessario esaminare il razionale della Gnatologia Classica per comprendere l'interazione tra piani e assi nel descrivere i movimenti condilari.

Il pantografo analogico è stato considerato un dispositivo capace di riprodurre con precisione i movimenti di confine dei tracciati condilari e di trasferirli su un articolatore completamente regolabile tramite le sue 6 piastrine.^[1]^[2]^[3]

Successivamente, si è riportato che anche il pantografo elettronico registrava i determinanti condilari con un intervallo accettabile (argomento trattato nei capitoli successivi).^[4]

Un determinante particolare del movimento condilare, la traslazione laterale immediata mandibolare (Movimento di Bennett), è stato oggetto di dibattito e confusione nella letteratura protesica.^[5] Tuttavia, una recente revisione della letteratura ha evidenziato una mancanza di prove sul significato clinico di questo movimento.^[6]

Nota sulla Precisione e Sugli Obiettivi dello Studio
Questo studio mira a fornire una comprensione concettuale dei principi cinematici coinvolti nella dinamica masticatoria, con un focus sulla biomeccanica mandibolare. Sebbene i calcoli siano stati eseguiti con rigore, potrebbero verificarsi discrepanze dovute a:

Approssimazioni nei dati numerici: Differenze nei valori cartesiani legate a variabili operative.

Limiti di rappresentazione: Uso di numeri approssimati per motivi pratici.

Finalità cliniche: Lo scopo è descrivere concetti piuttosto che ottenere precisione assoluta.

Figura 1: Cinematica mandibolare sul piano assiale rappresentata dai markers prelevati dallo strumento ogni 20 mSec. Questi punti rappresentano i condili laterotrusivi dal punto

L_{c}

e mediotrusivi

M_{c}

. Il Laterotrusive point (a sinistra) e il Mediotrusive point (a destra) tracciano la posizione dei condili della mandibola durante un movimento masticatorio laterale, che include movimenti complessi di traslazione e rotazione. I punti numerati (

1L_{c}

....

8L_{c}

) seguono il movimento del condilo laterotrusivo nel tempo, mentre i punti

1M_{c}

....

8M_{c}

seguono il condilo mediotrusivo. Nell'area del Molar point e dell' Incisal point sono rappresentati i percorsi occlusali durante la masticazione.

Passi Successivi

In questo capitolo, analizzeremo la cinematica dell'asse verticale ( $_{v}HA$ ) e il fenomeno masticatorio, rappresentandolo con tracciati estratti da lavori di riferimento come quello di Lund e Gibbs.^[7](Figura 1)

Descrizione della Calibrazione: da Pixel a Millimetri

La calibrazione di un'immagine per ottenere misurazioni accurate richiede l'attenzione a diversi fattori critici. Estrarre distanze da un'immagine può essere complesso, poiché la precisione dipende da:

Fattori di distorsione: Le immagini possono essere affette da distorsioni ottiche, che devono essere corrette calibrando la camera utilizzando, ad esempio, una scacchiera di riferimento.
Effetto prospettico: La scala di riferimento varia con la distanza dal piano di acquisizione. Per oggetti posti a diverse profondità, è necessario applicare fattori di scala specifici, calcolati utilizzando un modello come quello della pin-hole camera.
Distorsioni prospettiche: Queste possono essere corrette utilizzando ottiche telecentriche, particolarmente utili per applicazioni che richiedono un'elevata accuratezza, come nelle misurazioni spaziali o bioingegneristiche.

Con questa premessa, il fattore di scala utilizzato nel nostro studio rappresenta un'approssimazione valida nel contesto specifico delle immagini 2D acquisite in condizioni controllate. Tuttavia, per applicazioni più rigorose, come quelle descritte sopra, è necessario considerare strumenti e metodi avanzati per la calibrazione.

Calcolo della Distanza tra i Punti

Le coordinate dei punti sono:

$Q_{2}(525.3,-406)$ e $R_{2}(764.4,-407.1)$

La formula per la distanza euclidea è:

$d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}$

Sostituendo i valori:

$d={\sqrt {(764.4-525.3)^{2}+(-407.1-(-406))^{2}}}$

$d={\sqrt {(239.1)^{2}+(-1.1)^{2}}}$

$d={\sqrt {57121.81+1.21}}={\sqrt {57123.02}}\approx 239.02\,{\text{pixel}}$

Conversione della Scala in mm

Dato che il segmento di $239.02\,{\text{pixel}}$ equivale a $1\,{\text{cm}}=10\,{\text{mm}}$ , calcoliamo la conversione in mm/pixel:

${\text{Scala in mm/pixel}}={\frac {\text{Lunghezza reale (in mm)}}{\text{Distanza in pixel}}}={\frac {10}{239.02}}\approx 0.04184\,{\text{mm/pixel}}$

Quindi, ogni pixel nella figura corrisponde a circa:

$0.04184\,{\text{mm/pixel}}$ .

Esempio di Applicazione: Conversione Distanza in mm

Supponiamo di voler calcolare una distanza in mm. Ad esempio, se la distanza in pixel fosse $d=100\,{\text{pixel}}$ :

$d_{\text{mm}}=100\cdot 0.04184\approx 4.184\,{\text{mm}}$

Risultato Finale

La scala è:

$239.02\,{\text{pixel/cm}}$
$0.04184\,{\text{mm/pixel}}$

Questi valori possono essere usati per convertire qualsiasi distanza misurata in pixel nella figura in unità metriche come millimetri o centimetri.

Cinematica dei Condili

Traslazioni e Rotazioni dei Condili

Nel contesto del movimento mandibolare, i condili eseguono sia movimenti traslatori (spostamenti lineari) sia rotatori (movimenti angolari attorno a specifici assi). Questo doppio movimento, noto come rototraslazione, è fondamentale per comprendere la cinematica mandibolare.

Per descrivere la posizione e il movimento di ciascun condilo nel tempo, si utilizzano vettori di posizione, che variano in modulo e direzione a seguito del moto elicoidale. Il moto è descritto da una combinazione di spostamenti lineari e variazioni angolari che influenzano la posizione dei vettori nello spazio tridimensionale.

Vettori di Posizione del Condilo Laterotrusivo (Lavorante)

Il condilo laterotrusivo si trova sul lato in cui avviene la laterotrusione (spostamento laterale della mandibola). Durante il movimento, la sua posizione è descritta dal seguente vettore:

$P_{l}(t)=[X_{l}(t),Y_{l}(t),Z_{l}(t),\theta _{l}(t),\phi _{l}(t),\psi _{l}(t)]$

Dove:

$X_{l}(t),Y_{l}(t),Z_{l}(t)$ $X_{l}(t),Y_{l}(t),Z_{l}(t)$ : Spostamenti lineari lungo gli assi cartesiani:
- $X_{l}(t)$ : Spostamento antero-posteriore.
- $Y_{l}(t)$ : Spostamento latero-mediale.
- $Z_{l}(t)$ : Spostamento verticale.

$\theta _{l}(t)$ , $\phi _{l}(t)$ , $\psi _{l}(t)$ : Rotazioni angolari attorno agli assi $X$ , $Y$ e $Z$ , descritte con gli angoli di Eulero.

Adottiamo la convenzione $X,Y,Z$ , che segue l’ordine:

$\theta _{l}(t)$ : Rotazione attorno a $X$ (torsione laterale).
$\phi _{l}(t)$ : Rotazione attorno a $Y$ (apertura/chiusura).
$\psi _{l}(t)$ : Rotazione attorno a $Z$ (rotazione laterale/mediale).

Questa sequenza consente una descrizione univoca dell’orientamento del condilo nello spazio.

Figura 2: Tracciati cinematici masticatori sul piano sagittale.
Figura 3: Tracciati cinematici masticatori sul piano coronale.
Figura 4: Tracciati cinematici masticatori sul piano assiale.

Traslazione del Condilo Mediotrusivo

Il condilo mediotrusivo, sul lato opposto al movimento laterale, si muove principalmente con una traslazione anteriore e mediale nello spazio tridimensionale. La traslazione è descritta dal seguente vettore:

$T_{M}(t)={\begin{pmatrix}X_{M}(t)\\Y_{M}(t)\\Z_{M}(t)\end{pmatrix}}$

Dove:

$(X_{M}(t),Y_{M}(t),Z_{M}(t))$ : Coordinate temporali del condilo mediotrusivo nello spazio cartesiano.

Questo tipo di traslazione influenza significativamente i tracciati occlusali, generando variazioni di orientamento durante il ciclo masticatorio.

Descrizione delle misure lineari ed angolari

Rappresentazione scalare dei tracciati condilari

Descrizione delle distanze e delle direzioni

Di seguito sono riportate le distanze calcolate tra i punti rispetto al punto di partenza (punto 1, massima intercuspidazione), considerato punto di riferimento, e le relative direzioni nello spazio, utilizzando le coordinate corrette per gli assi $X$ (antero-posteriore) e $Y$ (latero-mediale).

Calcolo delle distanze tra i punti

Le coordinate dei punti estrapolate da Geogebra dopo calibrazione, per il condilo laterotrusivo, sono:

1L: $(58.3,-50.9)$
2L: $(59,-92.3)$
3L: $(46.3,-169.5)$
4L: $(44.1,-207.7)$
5L: $(38.4,-136.2)$
6L: $(36.4,-48.2)$
7L: $(44,-34.9)$
8L: $(52.9,-48)$

Fattore di scala: $0.04184\,{\text{mm/pixel}}$

Distanze rispetto a $1L_{c}$ :

$2L_{c}$ :

$d={\sqrt {(59-58.3)^{2}+(-92.3-(-50.9))^{2}}}={\sqrt {(0.7)^{2}+(-41.4)^{2}}}={\sqrt {0.49+1714.36}}\approx 41.41\,{\text{pixel}}$ $d=41.41\cdot 0.04184\approx 1.734\,{\text{mm}}$

$3L_{c}$ :

$d={\sqrt {(46.3-58.3)^{2}+(-169.5-(-50.9))^{2}}}={\sqrt {(-12)^{2}+(-118.6)^{2}}}={\sqrt {144+14063.96}}\approx 119.17\,{\text{pixel}}$ $d=119.17\cdot 0.04184\approx 4.99\,{\text{mm}}$

$4L_{c}$ :

$d={\sqrt {(44.1-58.3)^{2}+(-207.7-(-50.9))^{2}}}={\sqrt {(-14.2)^{2}+(-156.8)^{2}}}={\sqrt {201.64+24589.44}}\approx 157.43\,{\text{pixel}}$ $d=157.43\cdot 0.04184\approx 6.59\,{\text{mm}}$

$5L_{c}$ :

$d={\sqrt {(38.4-58.3)^{2}+(-136.2-(-50.9))^{2}}}={\sqrt {(-19.9)^{2}+(-85.3)^{2}}}={\sqrt {396.01+7275.09}}\approx 87.6\,{\text{pixel}}$ $d=87.6\cdot 0.04184\approx 3.66\,{\text{mm}}$

$6L_{c}$ :

$d={\sqrt {(36.4-58.3)^{2}+(-48.2-(-50.9))^{2}}}={\sqrt {(-21.9)^{2}+(2.7)^{2}}}={\sqrt {479.61+7.29}}\approx 22.06\,{\text{pixel}}$ $d=22.06\cdot 0.04184\approx 0.923\,{\text{mm}}$

$7L_{c}$ :

$d={\sqrt {(44-58.3)^{2}+(-34.9-(-50.9))^{2}}}={\sqrt {(-14.3)^{2}+(16)^{2}}}={\sqrt {204.49+256}}\approx 21.47\,{\text{pixel}}$ $d=21.47\cdot 0.04184\approx 0.898\,{\text{mm}}$

$8L_{c}$ :

$d={\sqrt {(52.9-58.3)^{2}+(-48-(-50.9))^{2}}}={\sqrt {(-5.4)^{2}+(2.9)^{2}}}={\sqrt {29.16+8.41}}\approx 6.13\,{\text{pixel}}$

$d=6.13\cdot 0.04184\approx 0.257\,{\text{mm}}$

↑ Curtis, D.A. ∙ Sorensen, J.A. Errors incurred in programming a fully adjustable articulator with a pantograph J Prosthet Dent. 1986; 55:427-429
↑ Clayton, J.A. ∙ Kotowicz, W.E. ∙ Zahler, J.M. Pantographic tracings of mandibular movements and occlusion J Prosthet Dent. 1971; 75:389-395
↑ Shields, J.M. ∙ Clayton, J.A. ∙ Sindledecker, L.D. Using pantographic tracings to detect TMJ and muscle dysfunctions J Prosthet Dent. 1978; 39:80-87
↑ Payne, J. Condylar determinants in a patient population: electronic pantograph assessment J Oral Rehabil. 1997; 24:157-163
↑ Bennett, N.G. A contribution to the study of the movements of the mandible Proc R Soc Med. 1908; 1:79-98
↑ Taylor, T.D. ∙ Bidra, A.S. ∙ Nazarova, E. ... Clinical significance of immediate mandibular lateral translation: A systematic review J Prosthet Dent. 2016; 115:412-418
↑ N A Wickwire, C H Gibbs, A P Jacobson, H C Lundeen. Chewing patterns in normal children. Angle Orthod. 1981 Jan;51(1):48-60.

[1] Curtis, D.A. ∙ Sorensen, J.A. Errors incurred in programming a fully adjustable articulator with a pantograph J Prosthet Dent. 1986; 55:427-429

[2] Clayton, J.A. ∙ Kotowicz, W.E. ∙ Zahler, J.M. Pantographic tracings of mandibular movements and occlusion J Prosthet Dent. 1971; 75:389-395

[3] Shields, J.M. ∙ Clayton, J.A. ∙ Sindledecker, L.D. Using pantographic tracings to detect TMJ and muscle dysfunctions J Prosthet Dent. 1978; 39:80-87

[4] Payne, J. Condylar determinants in a patient population: electronic pantograph assessment J Oral Rehabil. 1997; 24:157-163

[5] Bennett, N.G. A contribution to the study of the movements of the mandible Proc R Soc Med. 1908; 1:79-98

[6] Taylor, T.D. ∙ Bidra, A.S. ∙ Nazarova, E. ... Clinical significance of immediate mandibular lateral translation: A systematic review J Prosthet Dent. 2016; 115:412-418

[7] N A Wickwire, C H Gibbs, A P Jacobson, H C Lundeen. Chewing patterns in normal children. Angle Orthod. 1981 Jan;51(1):48-60.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

@@ Line 1: / Line 1: @@
 == Introduzione ==
-Nel capitolo precedente, ''[[Transverse Hinge Axis]]'', abbiamo introdotto la cinematica mandibolare concentrandoci sul piano sagittale, osservando come i movimenti di protrusione e retrusione della mandibola includano non solo traslazioni lungo l’asse <math>X</math>, ma anche rotazioni attorno all’asse <math>Y</math>. Questo movimento condilare si riflette in traiettorie curvilinee osservabili, ad esempio, nell'incisivo mandibolare, e rappresenta una combinazione di rotazioni e traslazioni nello spazio tridimensionale.
+Nel capitolo precedente, '[[Transverse Hinge Axis]]', abbiamo introdotto la cinematica mandibolare concentrandoci sul piano sagittale. Durante i movimenti di protrusione e retrusione, la mandibola non si muove esclusivamente lungo l'asse <math>X</math>, ma ruota attorno al centro dell'asse <math>Y</math>. Questo movimento condilare si manifesta anteriormente, dove l'incisivo mandibolare segue traiettorie curvilinee inverse, risultato di un complesso moto spaziale generato dalla rototraslazione sugli assi condilari. Lo spazio angolare risultante, noto come 'Spazio libero Interincisivo', è essenziale per consentire movimenti masticatori fluidi e senza ostacoli.
+Questo 'Spazio libero Interincisivo' riveste un ruolo cruciale nelle funzioni masticatorie. Tuttavia, strumenti come il Sirognatograph e i sistemi elettromagnetici tradizionali trascurano la componente rotazionale dei movimenti condilari, focalizzandosi principalmente sulle traslazioni. Sebbene ciò possa essere sufficiente per alcune registrazioni, tale approccio è limitato nel cogliere la complessità dei movimenti mandibolari a sei gradi di libertà.
 '''Cinematica Mandibolare a Sei Gradi di Libertà'''
-Il movimento mandibolare può essere descritto da un sistema tridimensionale con sei gradi di libertà: tre assi di traslazione (<math>X, Y, Z</math>) e tre assi di rotazione. Ogni condilo è associato a:
-* L'asse <math>Y</math> (latero-mediale) per la rotazione sull'asse cerniera trasversale (<math>tHA</math>).
-* L'asse <math>Z</math> (verticale) per la rotazione sull'asse cerniera verticale (<math>vHA</math>).
-* L'asse <math>X</math> (antero-posteriore) per la rotazione sull'asse cerniera orizzontale (<math>oHA</math>).
-I piani anatomici fondamentali (<math>(X,Y)</math>, <math>(X,Z)</math>, <math>(Y,Z)</math>) sono utilizzati per studiare le relazioni tra i movimenti articolari.
+Il movimento mandibolare avviene in uno spazio tridimensionale e può essere descritto come un complesso moto spaziale. Ogni condilo è associato a tre assi principali:
+* Asse <math>Y</math> (latero-mediale): Definisce la rotazione attorno all'asse cerniera trasversale (<math>_tHA</math>, transverse Hinge Axis).
+* **Asse <math>Z</math> (verticale):** Definisce la rotazione sull'asse cerniera verticale (<math>_vHA</math>).
+* **Asse <math>X</math> (antero-posteriore): Definisce la rotazione attorno all'asse cerniera orizzontale (<math>_oHA</math>).
+A ciascun asse corrisponde un piano di riferimento anatomico:
+* '''Piano sagittale:''' Mostra il tracciato condilare prodotto dal movimento di rototraslazione dell'asse trasversale (<math>_tHA</math>).
+* '''Piano coronale:''' Associato all'asse orizzontale (<math>_oHA</math>).
+* '''Piano assiale:''' Legato al movimento generato attorno all'asse verticale (<math>_vHA</math>, noto anche come asse cerniera verticale).
+Va evidenziato che un piano non è generato da un asse; un asse può al massimo essere contenuto in un piano o rappresentare una direzione. Più precisamente, il movimento di un asse genera una 'superficie rigata', che descrive le traiettorie spaziali risultanti.
+'''Asse cerniera verticale'''
+Ci concentreremo sull’asse cerniera verticale (<math>_vHA</math>) per la sua rilevanza nei sistemi di registrazione cinematici come pantografi, elegnatografi e assiografi. Tuttavia, è necessario esaminare il razionale della '''Gnatologia Classica''' per comprendere l'interazione tra piani e assi nel descrivere i movimenti condilari.
+* Il pantografo analogico è stato considerato un dispositivo capace di riprodurre con precisione i movimenti di confine dei tracciati condilari e di trasferirli su un articolatore completamente regolabile tramite le sue 6 piastrine.<ref>Curtis, D.A. ∙ Sorensen, J.A. Errors incurred in programming a fully adjustable articulator with a pantograph ''J Prosthet Dent.'' 1986; 55:427-429</ref><ref>Clayton, J.A. ∙ Kotowicz, W.E. ∙ Zahler, J.M. Pantographic tracings of mandibular movements and occlusion ''J Prosthet Dent.'' 1971; 75:389-395</ref><ref>Shields, J.M. ∙ Clayton, J.A. ∙ Sindledecker, L.D. Using pantographic tracings to detect TMJ and muscle dysfunctions ''J Prosthet Dent.'' 1978; 39:80-87</ref>
+* Successivamente, si è riportato che anche il pantografo elettronico registrava i determinanti condilari con un intervallo accettabile (argomento trattato nei capitoli successivi).<ref>Payne, J. Condylar determinants in a patient population: electronic pantograph assessment ''J Oral Rehabil.'' 1997; 24:157-163</ref>
+* Un determinante particolare del movimento condilare, la traslazione laterale immediata mandibolare (Movimento di Bennett), è stato oggetto di dibattito e confusione nella letteratura protesica.<ref>Bennett, N.G. A contribution to the study of the movements of the mandible ''Proc R Soc Med.'' 1908; 1:79-98</ref> Tuttavia, una recente revisione della letteratura ha evidenziato una mancanza di prove sul significato clinico di questo movimento.<ref>Taylor, T.D. ∙ Bidra, A.S. ∙ Nazarova, E. ... Clinical significance of immediate mandibular lateral translation: A systematic review ''J Prosthet Dent.'' 2016; 115:412-418</ref>
+<blockquote>'''Nota sulla Precisione e Sugli Obiettivi dello Studio'''
+Questo studio mira a fornire una comprensione concettuale dei principi cinematici coinvolti nella dinamica masticatoria, con un focus sulla biomeccanica mandibolare. Sebbene i calcoli siano stati eseguiti con rigore, potrebbero verificarsi discrepanze dovute a:
+* ''Approssimazioni nei dati numerici'': Differenze nei valori cartesiani legate a variabili operative.
+* ''Limiti di rappresentazione'': Uso di numeri approssimati per motivi pratici.
+* ''Finalità cliniche'': Lo scopo è descrivere concetti piuttosto che ottenere precisione assoluta.
+</blockquote>
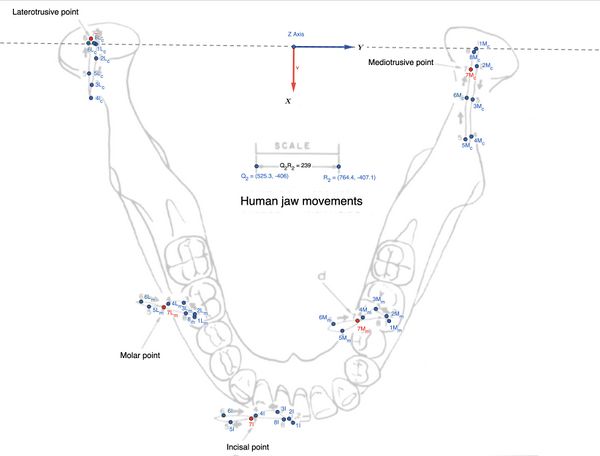
+[[File:Figura_1_finale_mod..jpg|center|thumb|600x600px|'''Figura 1:''' <small>Cinematica mandibolare sul piano assiale rappresentata dai markers prelevati dallo strumento ogni 20 mSec. Questi punti rappresentano i condili laterotrusivi dal punto <math>L_c </math> e mediotrusivi <math>M_c </math>.
+Il ''Laterotrusive point'' (a sinistra) e il ''Mediotrusive point'' (a destra) tracciano la posizione dei condili della mandibola durante un movimento masticatorio laterale, che include movimenti complessi di traslazione e rotazione. I punti numerati (<math>1L_c </math>....<math>8L_c </math>) seguono il movimento del condilo laterotrusivo nel tempo, mentre i punti <math>1M_c </math>....<math>8M_c </math> seguono il condilo mediotrusivo. Nell'area del ''Molar point'' e dell' ''Incisal point'' sono rappresentati i percorsi occlusali durante la masticazione.</small>]]
+'''Passi Successivi'''
+In questo capitolo, analizzeremo la cinematica dell'asse verticale (<math>_vHA</math>) e il fenomeno masticatorio, rappresentandolo con tracciati estratti da lavori di riferimento come quello di Lund e Gibbs.<ref>
+N A Wickwire, C H Gibbs, A P Jacobson, H C Lundeen. [https://pubmed.ncbi.nlm.nih.gov/6971588/ Chewing patterns in normal children]. Angle Orthod. 1981 Jan;51(1):48-60.</ref>(Figura 1)
+== Descrizione della Calibrazione: da Pixel a Millimetri ==
+La calibrazione di un'immagine per ottenere misurazioni accurate richiede l'attenzione a diversi fattori critici. Estrarre distanze da un'immagine può essere complesso, poiché la precisione dipende da:
+# ''Fattori di distorsione'': Le immagini possono essere affette da distorsioni ottiche, che devono essere corrette calibrando la camera utilizzando, ad esempio, una scacchiera di riferimento.
+# ''Effetto prospettico'': La scala di riferimento varia con la distanza dal piano di acquisizione. Per oggetti posti a diverse profondità, è necessario applicare fattori di scala specifici, calcolati utilizzando un modello come quello della pin-hole camera.
+# ''Distorsioni prospettiche'': Queste possono essere corrette utilizzando ottiche telecentriche, particolarmente utili per applicazioni che richiedono un'elevata accuratezza, come nelle misurazioni spaziali o bioingegneristiche.
+Con questa premessa, il fattore di scala utilizzato nel nostro studio rappresenta un'approssimazione valida nel contesto specifico delle immagini 2D acquisite in condizioni controllate. Tuttavia, per applicazioni più rigorose, come quelle descritte sopra, è necessario considerare strumenti e metodi avanzati per la calibrazione.
+'''Calcolo della Distanza tra i Punti'''
+Le coordinate dei punti sono:
+<math>Q_2(525.3, -406)</math> e <math>R_2(764.4, -407.1)</math>
+La formula per la distanza euclidea è:
+<math>d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}</math>
+Sostituendo i valori:
+<math>d = \sqrt{(764.4 - 525.3)^2 + (-407.1 - (-406))^2}</math>
+<math>d = \sqrt{(239.1)^2 + (-1.1)^2}</math>
+<math>d = \sqrt{57121.81 + 1.21} = \sqrt{57123.02} \approx 239.02 \, \text{pixel}</math>
+'''Conversione della Scala in mm'''
+Dato che il segmento di <math>239.02 \, \text{pixel}</math> equivale a <math>1 \, \text{cm} = 10 \, \text{mm}</math>, calcoliamo la conversione in mm/pixel:
+<math>\text{Scala in mm/pixel} = \frac{\text{Lunghezza reale (in mm)}}{\text{Distanza in pixel}} = \frac{10}{239.02} \approx 0.04184 \, \text{mm/pixel}</math>
+Quindi, ogni pixel nella figura corrisponde a circa:
+<math>0.04184 \, \text{mm/pixel}</math>.
+'''Esempio di Applicazione: Conversione Distanza in mm'''
+Supponiamo di voler calcolare una distanza in mm. Ad esempio, se la distanza in pixel fosse <math>d = 100 \, \text{pixel}</math>:
+<math>d_\text{mm} = 100 \cdot 0.04184 \approx 4.184 \, \text{mm} </math>
+'''Risultato Finale'''
+La scala è:
+* <math>239.02 \, \text{pixel/cm}</math>
+* <math>0.04184 \, \text{mm/pixel}</math>
+Questi valori possono essere usati per convertire qualsiasi distanza misurata in pixel nella figura in unità metriche come millimetri o centimetri.
+== Cinematica dei Condili ==
+'''Traslazioni e Rotazioni dei Condili'''
-== Coordinate dei Condili e Punti di Riferimento ==
+Nel contesto del movimento mandibolare, i condili eseguono sia movimenti traslatori (spostamenti lineari) sia rotatori (movimenti angolari attorno a specifici assi). Questo doppio movimento, noto come '''rototraslazione''', è fondamentale per comprendere la cinematica mandibolare.
-Consideriamo le coordinate iniziali:
-* Condilo laterotrusivo: <math>\mathbf{C}_L(0) = (0, 10, 0)</math>.
+Per descrivere la posizione e il movimento di ciascun condilo nel tempo, si utilizzano vettori di posizione, che variano in modulo e direzione a seguito del moto elicoidale. Il moto è descritto da una combinazione di spostamenti lineari e variazioni angolari che influenzano la posizione dei vettori nello spazio tridimensionale.
-* Condilo mediotrusivo: <math>\mathbf{C}_M(0) = (0, -10, 0)</math>.
-* Punto molare laterotrusivo: <math>\mathbf{M}_L(0) = (5, 5, -5)</math>.
+'''Vettori di Posizione del Condilo Laterotrusivo (Lavorante)'''
-* Punto incisale: <math>\mathbf{I}(0) = (0, 0, -10)</math>.
+Il condilo laterotrusivo si trova sul lato in cui avviene la laterotrusione (spostamento laterale della mandibola). Durante il movimento, la sua posizione è descritta dal seguente vettore:
-== Rotazione e Traslazione dei Condili ==
-=== Condilo Laterotrusivo ===
-La posizione al tempo <math>t</math> è:
 <math>
-\mathbf{C}_L(t) = \mathbf{R}_Z(\theta_L) \cdot \left(\mathbf{C}_L(0) - \mathbf{P}\right) + \mathbf{P} + \mathbf{d}_L
+P_l(t) = [X_l(t), Y_l(t), Z_l(t), \theta_l(t), \phi_l(t), \psi_l(t)]
 </math>
-Dove:
-* <math>\mathbf{R}_Z(\theta_L)</math>: matrice di rotazione attorno a <math>Z</math>.
+Dove:
-* <math>\mathbf{P}</math>: centro di rotazione (spesso origine del sistema).
+* <math>X_l(t), Y_l(t), Z_l(t)</math>: Spostamenti lineari lungo gli assi cartesiani:
-* <math>\mathbf{d}_L = (-d_L, 0, 0)</math>: traslazione retrusiva.
+** <math>X_l(t)</math>: Spostamento antero-posteriore.
+** <math>Y_l(t)</math>: Spostamento latero-mediale.
+** <math>Z_l(t)</math>: Spostamento verticale.
+* <math>\theta_l(t)</math>, <math>\phi_l(t)</math>, <math>\psi_l(t)</math>: Rotazioni angolari attorno agli assi <math>X</math>, <math>Y</math> e <math>Z</math>, descritte con gli angoli di Eulero.
+Adottiamo la convenzione <math>X,Y,Z</math>, che segue l’ordine:
+* <math>\theta_l(t)</math>: Rotazione attorno a <math>X</math> (torsione laterale).
+* <math>\phi_l(t)</math>: Rotazione attorno a <math>Y</math> (apertura/chiusura).
+* <math>\psi_l(t)</math>: Rotazione attorno a <math>Z</math> (rotazione laterale/mediale).
+Questa sequenza consente una descrizione univoca dell’orientamento del condilo nello spazio.
+<gallery mode="slideshow">
+File:Sirignathograph rotazione asse Y.jpg|'''Figura 2:''' Tracciati cinematici masticatori sul piano sagittale.
+File:Sirognathograph frontal angle.jpg|'''Figura 3:''' Tracciati cinematici masticatori sul piano coronale.
+File:Final HA 10.jpg|'''Figura 4:''' Tracciati cinematici masticatori sul piano assiale.
+</gallery>
+'''Traslazione del Condilo Mediotrusivo'''
+Il condilo mediotrusivo, sul lato opposto al movimento laterale, si muove principalmente con una traslazione anteriore e mediale nello spazio tridimensionale. La traslazione è descritta dal seguente vettore:
-=== Condilo Mediotrusivo ===
-Il movimento include rotazioni e traslazioni, descritte dalla formula di Rodrigues:
 <math>
-\mathbf{C}_M(t) = \mathbf{v} \cos(\theta) + (\mathbf{k} \times \mathbf{v}) \sin(\theta) + \mathbf{k} (\mathbf{k} \cdot \mathbf{v})(1 - \cos(\theta)) + \mathbf{d}_M
+T_M(t) = \begin{pmatrix}
-</math>
+X_M(t) \\
-Dove:
+Y_M(t) \\
-* <math>\mathbf{v}</math>: vettore da ruotare.
+Z_M(t)
-* <math>\mathbf{k} = (0, 0, 1)</math>: asse di rotazione.
+\end{pmatrix}
-* <math>\mathbf{d}_M</math>: traslazione mediale del condilo mediotrusivo.
+</math>
+Dove:
+* <math>(X_M(t), Y_M(t), Z_M(t))</math>: Coordinate temporali del condilo mediotrusivo nello spazio cartesiano.
+<blockquote>Questo tipo di traslazione influenza significativamente i tracciati occlusali, generando variazioni di orientamento durante il ciclo masticatorio.</blockquote>
-== Tracciati dei Punti di Interesse ==
+== Descrizione delle misure lineari ed angolari ==
-=== Punto Molare Laterotrusivo ===
-La posizione è influenzata dai condili e può essere descritta da:
+=== Rappresentazione scalare dei tracciati condilari ===
-<math>
-\mathbf{M}_L(t) = \mathbf{M}_L(0) + \alpha \cdot \mathbf{C}_L(t) + \beta \cdot \mathbf{C}_M(t)
+'''Descrizione delle distanze e delle direzioni'''
-</math>
-Con <math>\alpha</math> e <math>\beta</math> come coefficienti di influenza.
+Di seguito sono riportate le distanze calcolate tra i punti rispetto al punto di partenza (punto 1, massima intercuspidazione), considerato punto di riferimento, e le relative direzioni nello spazio, utilizzando le coordinate corrette per gli assi <math>X</math> (antero-posteriore) e <math>Y</math> (latero-mediale).
+'''Calcolo delle distanze tra i punti'''
+Le coordinate dei punti estrapolate da Geogebra dopo calibrazione, per il condilo laterotrusivo, sono:
+* 1L: <math>(58.3, -50.9)</math>
+* 2L: <math>(59, -92.3)</math>
+* 3L: <math>(46.3, -169.5)</math>
+* 4L: <math>(44.1, -207.7)</math>
+* 5L: <math>(38.4, -136.2)</math>
+* 6L: <math>(36.4, -48.2)</math>
+* 7L: <math>(44, -34.9)</math>
+* 8L: <math>(52.9, -48)</math>
+'''Fattore di scala:''' <math>0.04184 \, \text{mm/pixel}</math>
+Distanze rispetto a <math>1L_c</math>:
+'''<math>2L_c</math>:'''
+<math>d = \sqrt{(59 - 58.3)^2 + (-92.3 - (-50.9))^2} = \sqrt{(0.7)^2 + (-41.4)^2} = \sqrt{0.49 + 1714.36} \approx 41.41 \, \text{pixel}</math>  <math>d = 41.41 \cdot 0.04184 \approx 1.734 \, \text{mm}</math>
+'''<math>3L_c</math>:'''
+<math>d = \sqrt{(46.3 - 58.3)^2 + (-169.5 - (-50.9))^2} = \sqrt{(-12)^2 + (-118.6)^2} = \sqrt{144 + 14063.96} \approx 119.17 \, \text{pixel}</math>
+<math>d = 119.17 \cdot 0.04184 \approx 4.99 \, \text{mm}</math>
+'''<math>4L_c</math>:'''
+<math>d = \sqrt{(44.1 - 58.3)^2 + (-207.7 - (-50.9))^2} = \sqrt{(-14.2)^2 + (-156.8)^2} = \sqrt{201.64 + 24589.44} \approx 157.43 \, \text{pixel}</math>
+<math>d = 157.43 \cdot 0.04184 \approx 6.59 \, \text{mm}</math>
+'''<math>5L_c</math>:'''
+<math>d = \sqrt{(38.4 - 58.3)^2 + (-136.2 - (-50.9))^2} = \sqrt{(-19.9)^2 + (-85.3)^2} = \sqrt{396.01 + 7275.09} \approx 87.6 \, \text{pixel}</math>
+<math>d = 87.6 \cdot 0.04184 \approx 3.66 \, \text{mm}</math>
-=== Punto Incisale ===
+'''<math>6L_c</math>:'''
-Il tracciato incisale dipende dal movimento globale mandibolare:
-<math>
-\mathbf{I}(t) = \mathbf{I}(0) + \gamma \cdot \mathbf{C}_L(t) + \delta \cdot \mathbf{C}_M(t)
-</math>
-Con <math>\gamma</math> e <math>\delta</math> che riflettono i contributi condilari.
-=== Punto Molare Mediotrusivo ===
+<math>d = \sqrt{(36.4 - 58.3)^2 + (-48.2 - (-50.9))^2} = \sqrt{(-21.9)^2 + (2.7)^2} = \sqrt{479.61 + 7.29} \approx 22.06 \, \text{pixel}</math>
-Il punto molare mediotrusivo si sposta secondo:
+<math>d = 22.06 \cdot 0.04184 \approx 0.923 \, \text{mm}</math>
-<math>
-\mathbf{M}_M(t) = \mathbf{M}_M(0) + \alpha' \cdot \mathbf{C}_L(t) + \beta' \cdot \mathbf{C}_M(t)
-</math>
-== Sintesi dei Risultati ==
+'''<math>7L_c</math>:'''
-{| class="wikitable"
-! Punto !! Distanza da P<sub>1</sub> (mm) !! Direzione X !! Direzione Y !! Angolo (°)
-|-
-| Condilo laterotrusivo || 15.75 || Retrusiva || Laterale || 42.44
-|-
-| Punto molare laterotrusivo || 9.1 || Laterale || Laterale || 73.32
-|-
-| Punto incisale || 13.84 || Retrusiva || Laterale || 85.09
-|-
-| Punto molare mediotrusivo || 8.99 || Protrusiva || Mediale || 91.33
-|}
-Le distanze e gli angoli sono stati calcolati utilizzando la distanza euclidea e il prodotto scalare, descrivendo con precisione i movimenti lineari e angolari.
-== Discussioni e Conclusioni ==
+<math>d = \sqrt{(44 - 58.3)^2 + (-34.9 - (-50.9))^2} = \sqrt{(-14.3)^2 + (16)^2} = \sqrt{204.49 + 256} \approx 21.47 \, \text{pixel}</math>
-La cinematica mandibolare a sei gradi di libertà mostra che i movimenti condilari influenzano in modo complesso i punti di riferimento mandibolari. In particolare:
+<math>d = 21.47 \cdot 0.04184 \approx 0.898 \, \text{mm}</math>
-. Il condilo laterotrusivo segue un movimento combinato di rotazione retrusiva e traslazione.
-. Il condilo mediotrusivo contribuisce significativamente al movimento orbitante.
-. I tracciati dei punti molare e incisale riflettono l’interazione tra i condili.
-La comprensione di queste dinamiche è cruciale per:
+'''<math>8L_c</math>:'''
-* Diagnosticare disfunzioni temporomandibolari.
-* Pianificare interventi terapeutici e riabilitativi.
-* Modellare i movimenti mandibolari per simulazioni biomeccaniche.
-La cinematica mandibolare non può essere semplificata considerando l'asse verticale <math>Z</math> come un riferimento statico, poiché il movimento tridimensionale richiede un approccio integrato che tenga conto delle interazioni tra i condili.
+<math>d = \sqrt{(52.9 - 58.3)^2 + (-48 - (-50.9))^2} = \sqrt{(-5.4)^2 + (2.9)^2} = \sqrt{29.16 + 8.41} \approx 6.13 \, \text{pixel}</math>
-----
+<math>d = 6.13 \cdot 0.04184 \approx 0.257 \, \text{mm}</math>
-{{Bib}}