Difference between revisions of "Store:46laterotrusivo"

Latest revision as of 18:44, 13 December 2024

Molare Laterotrusivo

Il testo descrive un'analisi dettagliata dei movimenti articolari del molare ipsilaterale al condilo laterotrusivo (Figura 3 e Tabella 2). L'analisi si basa sul calcolo delle distanze tra punti e degli angoli formati tra i vettori utilizzando la trigonometria vettoriale.

Tabella 2
Tracciato masticatorio	Markers	Distanza (mm)	Direzione in X (antero-posteriore)	Direzione dinamica (Y - latero-mediale)
	2	0.86	Indietro	Lateralizzazione
	3	5.47	Indietro	Lateralizzazione
	4	8.48	Indietro	Lateralizzazione
	5	13.52	Indietro	Lateralizzazione
	6	16.43	Indietro	Inversione
	7*	9.05	Indietro	Medializzazione
	8	2.72	Indietro	Medializzazione

Osservando la figura e la tabella, possiamo estrapolare le distanze e le direzioni dei punti marcati. Nello specifico, la distanza del punto $7^{*}$ rispetto al punto iniziale è stata calcolata come circa $9.05\,{\text{mm}}$ , con un angolo formato tra i vettori pari a $72.80^{\circ }$ .

**Iter matematico per il calcolo dell'angolo:**

Il vettore tra il punto $P1_{m}$ e il punto $P7_{m}$ :

${\vec {AB}}=P7_{m}-P1_{m}=(147.2,-380.7)-(185.2,-392.7)=(-38.0,12.0)$

Il vettore tra il punto $P1_{m}$ e il punto di riferimento $R_{p}$ :

${\vec {AC}}=R_{p}-P1_{m}=(185.6,-308.9)-(185.2,-392.7)=(0.4,83.8)$

Calcolo del coseno dell'angolo: $\cos(\theta )={\frac {{\vec {AB}}\cdot {\vec {AC}}}{|{\vec {AB}}|\cdot |{\vec {AC}}|}}$ Sostituendo i valori: $\cos(\theta )={\frac {990.4}{39.87\cdot 83.80}}\approx 0.2964$ .

Infine, l'angolo $\theta$ è calcolato tramite la funzione arccoseno: $\theta =\arccos(0.2964)\approx 72.80^{\circ }$ .

@@ Line 1: / Line 1: @@
-===Molare laterotrusivo===
-Il testo descrive un'analisi dettagliata dei movimenti articolari del molare ipsilaterale al condilo laterotrusivo (Figura 3 e tabella 2)e coinvolge vari punti nello spazio 2D per calcolare distanze e angoli utilizzando la trigonometria vettoriale.
+===Molare Laterotrusivo===
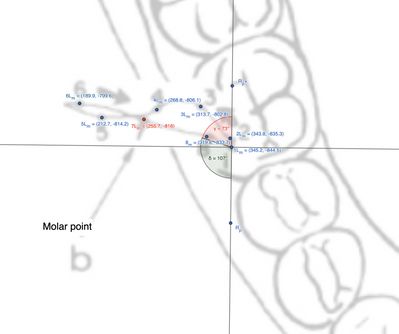
-[[File:Angolo molare.jpg|left|thumb|'''Figura 3:''' Rappresentazione delle distanze tra punti nel molare ipsilaterale alla laterotrusione]]
+Il testo descrive un'analisi dettagliata dei movimenti articolari del molare ipsilaterale al condilo laterotrusivo (Figura 3 e Tabella 2). L'analisi si basa sul calcolo delle distanze tra punti e degli angoli formati tra i vettori utilizzando la trigonometria vettoriale.
-{| class="wikitable"
-! colspan="4" |Tabella 2
+<Center>
+{|
+! colspan="5" |Tabella 2
 |-
-!Point
+!Tracciato masticatorio
-!Distance
+!Markers
-(mm)
+!Distanza (mm)
 !Direzione in X
 (antero-posteriore)
-!Direzione in Y
+!Direzione dinamica
-(latero-mediale)
+(Y - latero-mediale)
 |-
+| rowspan="8" |[[File:Figura Molare laterotrusivo.jpg|center|400x400px|'''Figura 3:''' Rappresentazione delle distanze tra punti nel molare ipsilaterale alla laterotrusione]]
 |2
-|0.874 mm
+|0.86
 |Indietro
-|Laterale
+|Lateralizzazione
 |-
 |3
-|5.442 mm
+|5.47
 |Indietro
-|Laterale
+|Lateralizzazione
 |-
-| 4
+|4
-|8.464 mm
+|8.48
-| Indietro
+|Indietro
-|Laterale
+|Lateralizzazione
 |-
 |5
-|13.448 mm
+|13.52
 |Indietro
-|Laterale
+|Lateralizzazione
 |-
 |6
-|16.059 mm
+|16.43
 |Indietro
-|Laterale
+|Inversione
 |-
-| 7*
+|7*
-|9.199 mm
+|9.05
 |Indietro
-|Laterale
+|Medializzazione
 |-
 |8
-|2.77 mm
+|2.72
 |Indietro
-|Laterale
+|Medializzazione
 |-
-| colspan="4" |Rappresentazione delle distanze e dell'angolo formato tra i puntimarcati nel ciclo masticatorio riferiti al punto 1 di massima intercuspidazione. IL punto 7* è il punto considerato per lo specifico calcolo del molare laterotrusivo
+| colspan="4" |
 |}
-Il formalismo matematico è lo stesso di quello precedentemente descritto e inserito nella nota informativa {{Tooltip|2=Nel contesto della nostra analisi, abbiamo tre punti nello spazio 2D che ci interessano: Coordinate <math> P1_{m}</math> del punto 1 del molare ipsilaterale al condilo latorotrusivo:<math>(345.2, -844.5) </math> *Coordinate <math>P7_{m}</math> del punto 7 del molare ipsilaterale al condilo latorotrusivo: <math>(255.7, -816)  </math> *Coordinate <math>R_p</math> del punto di riferimento del condilo mediotrusivo: <math>(347.7, -682.7)</math> Questi punti rappresentano tre posizioni specifiche all'interno di un sistema articolare che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti <math>P1_{m}</math> e <math>P7_{m}</math>, e il segmento che unisce i punti <math>P1_{m}</math> e <math>R_p</math>. Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio.'''Iter matematico per il calcolo dell'angolo''' L'angolo tra due segmenti può essere calcolato utilizzando la **trigonometria vettoriale** e, in particolare, il **prodotto scalare**. Questo metodo è utile quando vogliamo determinare la relazione angolare tra due movimenti distinti nello spazio. {{Tooltip|'''Definizione dei vettori'''| *Il vettore tra il punto <math>P1_{m}</math> e il punto <math>P7_{m}</math>: <math>\vec{AB} = P7_{m} -P1_{m} = (255.7, -816) - (345.2, -844.5) = (-89.5, 28.5)</math> *Il vettore tra il punto <math>P1_{m}</math> e il punto <math>H3 _{m}</math>: <math>\vec{AC} = \vec{R_p} - \vec{P_1} = (347.7, -682.7) - (345.2, -844.5) = (2.5, 161.8)</math>|2}}
+</Center>
-Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti:  {{Tooltip|'''Prodotto scalare'''|Sostituendo i valori calcolati: <math>\vec{AB} \cdot \vec{AC} = (-89.5) \cdot (2.5) + (28.5) \cdot (161.8) = -223.75 + 4601.3 = 4377.55</math> |2}} Il **prodotto scalare** tra due vettori <math>\vec{AB}</math> e <math>\vec{AC }</math> è dato dalla formula: <math>\vec{AB} \cdot \vec{AC} = AB_x \cdot AC_x + AB_y \cdot AC_y</math>{{Tooltip|'''Calcolo delle norme'''| <math>|\vec{AB}| = \sqrt{AB_x^2 + AB_y^2} = \sqrt{(-89.5)^2 + (28.5)^2} = \sqrt{8010.25 + 812.25} = \sqrt{8822.5} \approx 93.96</math> <math>|\vec{AC}| = \sqrt{AC_x^2 + AC_y^2} = \sqrt{(2.5)^2 + (161.8)^2} = \sqrt{6.25 + 26178.44} = \sqrt{26184.69} \approx 161.78</math>.|2}} Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore {{Tooltip|'''Calcolo dell'angolo'''|<math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}</math> Sostituendo i valori: <math>\cos(\theta) = \frac{4377.55}{93.96 \cdot 161.78} = \frac{4377.55}{15193.68} \approx 0.288</math>|2}} Ora possiamo usare la formula per il coseno dell'angolo tra i due vettori:  Infine, l'angolo <math>\theta</math> è calcolato tramite la funzione arcoseno: <math>\theta = \arccos(0.288) \approx 73.32^\circ</math> '''Motivo dell'analisi''' L'obiettivo dell'analisi è determinare l'angolo tra due movimenti all'interno di un sistema articolare, in particolare nell'area di studio della cinematica masticatoria.}} ed il risultato lineare ed angolare è di <math>9.1 </math> mm rispetto al punto <math>7^* </math> ed il coseno dell'angolo è stato calcolato come <math>0.288 </math> , con l'angolo risultante approssimativamente pari a <math>
-.32^\circ</math>.
-== Conclusione della cinematica del molare laterotrusivo ==
+Osservando la figura e la tabella, possiamo estrapolare le distanze e le direzioni dei punti marcati. Nello specifico, la distanza del punto <math>7^*</math> rispetto al punto iniziale è stata calcolata come circa <math>9.05 \, \text{mm}</math>, con un angolo formato tra i vettori pari a <math>72.80^\circ</math>.
-L'analisi del movimento articolare del molare ipsilaterale al condilo laterotrusivo fornisce una comprensione dettagliata delle dinamiche masticatorie laterali, con particolare attenzione agli spostamenti lineari e angolari che avvengono durante il movimento laterotrusivo. Utilizzando la trigonometria vettoriale e il prodotto scalare, è stato possibile calcolare la distanza e l'angolo tra i punti di riferimento selezionati, ottenendo risultati significativi che descrivono la traiettoria e l'orientamento del molare in relazione alla struttura condilare.
-In termini di spostamento lineare, il molare laterotrusivo mostra una distanza di circa <math>9.1</math>  mm rispetto al punto di massima intercuspidazione, rappresentato dal punto <math>7^*</math>. Questo movimento retrattivo e laterale riflette le forze e i vincoli strutturali imposti dalla morfologia condilare e dall'interazione con il condilo mediotrusivo, che influenzano la traiettoria del molare durante la funzione masticatoria.
+{{Tooltip|2=**Iter matematico per il calcolo dell'angolo:**
+* Il vettore tra il punto <math>P1_m</math> e il punto <math>P7_m</math>:
+<math>\vec{AB} = P7_m - P1_m = (147.2, -380.7) - (185.2, -392.7) = (-38.0, 12.0)</math>
+* Il vettore tra il punto <math>P1_m</math> e il punto di riferimento <math>R_p</math>:
+<math>\vec{AC} = R_p - P1_m = (185.6, -308.9) - (185.2, -392.7) = (0.4, 83.8)</math>
-Dal punto di vista angolare, il coseno dell'angolo calcolato tra i segmenti definiti è stato di <math>0.288</math>, che corrisponde a un angolo di <math>73.32^\circ</math>. Questo valore angolare offre informazioni fondamentali sulla direzione del movimento laterale e sul grado di deviazione del molare rispetto all'asse laterale di riferimento. Un angolo di questa entità indica una significativa deviazione laterale, suggerendo un elevato grado di libertà del molare durante il movimento, condizionato dalla tensione muscolare e dalla geometria articolare.
+Calcolo del coseno dell'angolo:
+<math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}</math>
+Sostituendo i valori:
+<math>\cos(\theta) = \frac{990.4}{39.87 \cdot 83.80} \approx 0.2964</math>.
-L'approccio matematico adottato permette non solo di quantificare lo spostamento, ma anche di inferire la qualità del movimento articolare, supportando così valutazioni cliniche che possono guidare sia diagnosi di anomalie masticatorie che interventi di riabilitazione mirati. In sintesi, i dati emersi da questa analisi costituiscono un'importante base di riferimento per comprendere i meccanismi biomeccanici sottostanti ai movimenti mandibolari e per migliorare la precisione dei trattamenti nell'ambito della riabilitazione masticatoria e della gestione dei disturbi temporomandibolari.
+Infine, l'angolo <math>\theta</math> è calcolato tramite la funzione arccoseno:
+<math>\theta = \arccos(0.2964) \approx 72.80^\circ</math>.}}