Difference between revisions of "Store:QLMde02"
Tags: Mobile web edit Mobile edit Visual edit |
|||
| Line 1: | Line 1: | ||
== | == Einführung == | ||
Die mathematischen Standardmethoden wurden ursprünglich entwickelt, um der klassischen Physik zu dienen. Die Realanalyse diente als mathematische Grundlage der Newtonschen Mechanik (Newton, 1687)<ref>{{cita libro | |||
| autore = Newton Isaac | | autore = Newton Isaac | ||
| titolo = Philosophiae naturalis principia mathematica | | titolo = Philosophiae naturalis principia mathematica | ||
| Line 16: | Line 16: | ||
| LCCN = | | LCCN = | ||
| OCLC = | | OCLC = | ||
}}</ref> ( | }}</ref> (und später des Hamiltonschen Formalismus); die klassische statistische Mechanik stimulierte den maßtheoretischen Ansatz der Wahrscheinlichkeitstheorie, formalisiert in Kolmogorovs Axiomatik (Kolmogorov, 1933)<ref>Kolmogorov A.N.Grundbegriffe Der Wahrscheinlichkeitsrechnung. Springer-Verlag, Berlin (1933)</ref>. Das Verhalten biologischer Systeme unterscheidet sich jedoch wesentlich vom Verhalten mechanischer Systeme, etwa starrer Körper, Gasmoleküle oder Flüssigkeiten. Obwohl die „klassische Mathematik“ immer noch die entscheidende Rolle bei der biologischen Modellierung spielt, scheint sie daher die reiche Komplexität von Biosystemen und Besonderheiten ihres Verhaltens – im Vergleich zu mechanischen Systemen – nicht vollständig beschreiben zu können. Neue mathematische Methoden zur Modellierung von Biosystemen sind gefragt.(a,b) | ||
In | In diesem Artikel stellen wir die Anwendungen des mathematischen Formalismus der Quantenmechanik und seiner Methodik zur Modellierung des Verhaltens von Biosystemen vor.(c) Die letzten Jahre waren gekennzeichnet durch eine Explosion des Interesses an Anwendungen der Quantentheorie außerhalb der Physik, insbesondere in der kognitiven Psychologie, Entscheidungsfindung, Informationsverarbeitung im Gehirn, Molekularbiologie, Genetik und Epigenetik und Evolutionstheorie.4 Wir nennen die entsprechenden Modelle quantenartig. Sie zielen nicht auf die Mikromodellierung echter quantenphysikalischer Prozesse in Biosystemen ab, etwa in Zellen oder Gehirnen (vgl. zu biologischen Anwendungen echter quantenphysikalischer Theorie Penrose 1989<ref>Penrose R. The Emperor’S New Mind Oxford Univ. Press, New-York (1989)</ref>, Umezawa 1993<ref>Umezawa H. Advanced Field Theory: Micro, Macro and Thermal Concepts AIP, New York (1993)</ref>, Hameroff 1994<ref>Hameroff S. Quantum coherence in microtubules. a neural basis for emergent con- sciousness? J. Cons. Stud., 1 (1994)</ref>, Vitiello 1995<ref>Vitiello G. Dissipation and memory capacity in the quantum brain model Internat. J. Modern Phys. B, 9 (1995), p. 973</ref>, Vitiello 2001<ref>Vitiello G. My Double Unveiled: The Dissipative Quantum Model of Brain, Advances in Consciousness Research, John Benjamins Publishing Company(2001)</ref>, Arndt et al., 2009<ref>Arndt M., Juffmann T., Vedral V. Quantum physics meets biology HFSP J., 3 (6) (2009), pp. 386-400, 10.2976/1.3244985</ref>, Bernroider und Summhammer 2012<ref>Bernroider G., Summhammer J. Can quantum entanglement between ion transition states effect action potential initiation? Cogn. Comput., 4 (2012), pp. 29-37</ref>, Bernroider 2017<ref>Bernroider G. Neuroecology: Modeling neural systems and environments, from the quantum to the classical level and the question of consciousness J. Adv. Neurosci. Res., 4 (2017), pp. 1-9</ref>). Quantenähnliche Modellierung arbeitet aus Sicht der Quantentheorie als Messtheorie. Dies ist der ursprüngliche Standpunkt Bohrs, der zur Kopenhagener Interpretation der Quantenmechanik führte (siehe Plotnitsky, 2009<ref>Plotnitsky A. Epistemology and Probability: Bohr, Heisenberg, SchrÖdinger and the Nature of Quantum-Theoretical Thinking Springer, Berlin, Germany; New York, NY, USA (2009</ref> für eine detaillierte und klare Darstellung von Bohrs Ansichten). Eine der wichtigsten Bio-Spezialitäten ist die Berücksichtigung von Selbstmessungen, die Biosysteme an sich selbst durchführen. In unserer Modellierung wird die Fähigkeit zur Durchführung von Selbstmessungen als grundlegendes Merkmal biologischer Funktionen betrachtet (siehe Abschnitt 8.2 und Artikel Khrennikov et al., 2018<ref name=":0">Khrennikov A., Basieva I., PothosE.M., Yamato I. Quantum Probability in Decision Making from Quantum Information Representation of Neuronal States, Sci. Rep., 8 (2018), Article 16225</ref>). | ||
Quantenähnliche Modelle (Khrennikov, 2004b<ref>Khrennikov A. On quantum-like probabilistic structure of mental information Open Syst. Inf. Dyn., 11 (3) (2004), pp. 267-275</ref>) spiegeln die Merkmale biologischer Prozesse wider, die natürlicherweise mit dem Quantenformalismus übereinstimmen. Bei einer solchen Modellierung ist es nützlich, die Quanteninformationstheorie zu untersuchen, die nicht nur auf die Mikrowelt der Quantensysteme angewendet werden kann. Im Allgemeinen müssen Systeme, die Informationen auf quantenähnliche Weise verarbeiten, keine quantenphysikalischen Systeme sein; insbesondere können sie makroskopische Biosysteme sein. Überraschenderweise kann dieselbe mathematische Theorie auf allen biologischen Ebenen angewendet werden: von Proteinen, Zellen und Gehirnen bis hin zu Menschen und Ökosystemen; wir können von Quanteninformationsbiologie sprechen (Asano et al., 2015a<ref name=":Asano et al., 2015a">Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Quantum information biology: from information interpretation of quantum mechanics to applications in molecular biology and cognitive psychology Found. Phys., 45 (10) (2015), pp. 1362-1378</ref>). | |||
In | In der quantenähnlichen Modellierung wird die Quantentheorie als Kalkül zur Vorhersage und Transformation von Wahrscheinlichkeiten betrachtet. Die Quantenwahrscheinlichkeitsrechnung (QP) (Abschnitt 2) unterscheidet sich wesentlich von der klassischen Wahrscheinlichkeitsrechnung (CP), die auf Kolmogorovs Axiomatik basiert (Kolmogorov, 1933<ref name=":2">Kolmogorov A.N. Grundbegriffe Der Wahrscheinlichkeitsrechnung Springer-Verlag, Berlin (1933)</ref>). In CP werden Zustände von Zufallssystemen durch Wahrscheinlichkeitsmaße und Observables durch Zufallsvariablen dargestellt; in QP werden Zustände zufälliger Systeme durch normalisierte Vektoren in einem komplexen Hilbert-Raum (reine Zustände) oder allgemein durch Dichteoperatoren (gemischte Zustände) dargestellt.5 Superpositionen, die durch reine Zustände dargestellt werden, werden verwendet, um Unsicherheiten zu modellieren, die noch nicht durch eine Messung aufgelöst wurden. Die Verwendung von Überlagerungen in der Biologie wird durch Abb. 1 veranschaulicht (siehe Abschnitt 10 und Artikel Khrennikov et al., 2018<ref name=":0" /> für das entsprechende Modell). Das aus einer Beobachtung resultierende QP-Update basiert auf dem Projektionspostulat oder allgemeineren Transformationen von Quantenzuständen – im Rahmen der Theorie von Quanteninstrumenten (Davies und Lewis, 1970<ref name=":3">Davies E.B., Lewis J.T. An operational approach to quantum probability Comm. Math. Phys., 17 (1970), pp. 239-260</ref>, Davies, 1976<ref name=":4">Davies E.B. Quantum Theory of Open Systems. Academic Press, London (1976)</ref>, Ozawa, 1984<ref name=":5">Ozawa M. Quantum measuring processes for continuous observables J. Math. Phys., 25 (1984), pp. 79-87</ref>, Yuen, 1987<ref name=":6">Yuen, H. P., 1987. Characterization and realization of general quantum measurements. M. Namiki and others (ed.) Proc. 2nd Int. Symp. Foundations of Quantum Mechanics, pp. 360–363.</ref>, Ozawa , 1997<ref name=":7">Ozawa M. An operational approach to quantum state reduction Ann. Phys., NY, 259 (1997), pp. 121-137</ref>, Ozawa, 2004<ref name=":8">Ozawa M. Uncertainty relations for noise and disturbance in generalized quantum measurements Ann. Phys., NY, 311 (2004), pp. 350-416</ref>, Okamura und Ozawa, 2016<ref name=":9">Okamura K., Ozawa M. Measurement theory in local quantum physics J. Math. Phys., 57 (2016), Article 015209</ref>) (Abschnitt 3). | ||
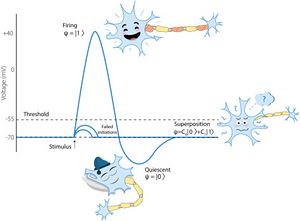
[[File:Schrodinger 1.jpeg|left|thumb|Fig. 1. Illustration for quantum-like representation of uncertainty generated by neuron’s action potential (originally published in Khrennikov et al. (2018)).]] | [[File:Schrodinger 1.jpeg|left|thumb|Fig. 1. Illustration for quantum-like representation of uncertainty generated by neuron’s action potential (originally published in Khrennikov et al. (2018)).]] | ||
Wir betonen, dass die quantenähnliche Modellierung die Rolle der Bequemlichkeit und Einfachheit der Quantendarstellung von Zuständen und Observablen erhöht. (Wir ignorieren pragmatisch das Problem der Wechselbeziehung von CP und QP.) Insbesondere hat der Quantenzustandsraum die lineare Struktur und lineare Modelle sind einfacher. Der Übergang von der klassischen nichtlinearen Dynamik elektrochemischer Prozesse in Biosystemen zur quantenlinearen Dynamik beschleunigt wesentlich die Zustandsentwicklung (Abschnitt 8.4). In diesem Rahmen ist „Zustand“ jedoch der Quanteninformationszustand eines Biosystems, der zur Verarbeitung spezieller Quantenunsicherheit verwendet wird (Abschnitt 8.2). | |||
Latest revision as of 11:44, 12 April 2023
Einführung
Die mathematischen Standardmethoden wurden ursprünglich entwickelt, um der klassischen Physik zu dienen. Die Realanalyse diente als mathematische Grundlage der Newtonschen Mechanik (Newton, 1687)[1] (und später des Hamiltonschen Formalismus); die klassische statistische Mechanik stimulierte den maßtheoretischen Ansatz der Wahrscheinlichkeitstheorie, formalisiert in Kolmogorovs Axiomatik (Kolmogorov, 1933)[2]. Das Verhalten biologischer Systeme unterscheidet sich jedoch wesentlich vom Verhalten mechanischer Systeme, etwa starrer Körper, Gasmoleküle oder Flüssigkeiten. Obwohl die „klassische Mathematik“ immer noch die entscheidende Rolle bei der biologischen Modellierung spielt, scheint sie daher die reiche Komplexität von Biosystemen und Besonderheiten ihres Verhaltens – im Vergleich zu mechanischen Systemen – nicht vollständig beschreiben zu können. Neue mathematische Methoden zur Modellierung von Biosystemen sind gefragt.(a,b)
In diesem Artikel stellen wir die Anwendungen des mathematischen Formalismus der Quantenmechanik und seiner Methodik zur Modellierung des Verhaltens von Biosystemen vor.(c) Die letzten Jahre waren gekennzeichnet durch eine Explosion des Interesses an Anwendungen der Quantentheorie außerhalb der Physik, insbesondere in der kognitiven Psychologie, Entscheidungsfindung, Informationsverarbeitung im Gehirn, Molekularbiologie, Genetik und Epigenetik und Evolutionstheorie.4 Wir nennen die entsprechenden Modelle quantenartig. Sie zielen nicht auf die Mikromodellierung echter quantenphysikalischer Prozesse in Biosystemen ab, etwa in Zellen oder Gehirnen (vgl. zu biologischen Anwendungen echter quantenphysikalischer Theorie Penrose 1989[3], Umezawa 1993[4], Hameroff 1994[5], Vitiello 1995[6], Vitiello 2001[7], Arndt et al., 2009[8], Bernroider und Summhammer 2012[9], Bernroider 2017[10]). Quantenähnliche Modellierung arbeitet aus Sicht der Quantentheorie als Messtheorie. Dies ist der ursprüngliche Standpunkt Bohrs, der zur Kopenhagener Interpretation der Quantenmechanik führte (siehe Plotnitsky, 2009[11] für eine detaillierte und klare Darstellung von Bohrs Ansichten). Eine der wichtigsten Bio-Spezialitäten ist die Berücksichtigung von Selbstmessungen, die Biosysteme an sich selbst durchführen. In unserer Modellierung wird die Fähigkeit zur Durchführung von Selbstmessungen als grundlegendes Merkmal biologischer Funktionen betrachtet (siehe Abschnitt 8.2 und Artikel Khrennikov et al., 2018[12]).
Quantenähnliche Modelle (Khrennikov, 2004b[13]) spiegeln die Merkmale biologischer Prozesse wider, die natürlicherweise mit dem Quantenformalismus übereinstimmen. Bei einer solchen Modellierung ist es nützlich, die Quanteninformationstheorie zu untersuchen, die nicht nur auf die Mikrowelt der Quantensysteme angewendet werden kann. Im Allgemeinen müssen Systeme, die Informationen auf quantenähnliche Weise verarbeiten, keine quantenphysikalischen Systeme sein; insbesondere können sie makroskopische Biosysteme sein. Überraschenderweise kann dieselbe mathematische Theorie auf allen biologischen Ebenen angewendet werden: von Proteinen, Zellen und Gehirnen bis hin zu Menschen und Ökosystemen; wir können von Quanteninformationsbiologie sprechen (Asano et al., 2015a[14]).
In der quantenähnlichen Modellierung wird die Quantentheorie als Kalkül zur Vorhersage und Transformation von Wahrscheinlichkeiten betrachtet. Die Quantenwahrscheinlichkeitsrechnung (QP) (Abschnitt 2) unterscheidet sich wesentlich von der klassischen Wahrscheinlichkeitsrechnung (CP), die auf Kolmogorovs Axiomatik basiert (Kolmogorov, 1933[15]). In CP werden Zustände von Zufallssystemen durch Wahrscheinlichkeitsmaße und Observables durch Zufallsvariablen dargestellt; in QP werden Zustände zufälliger Systeme durch normalisierte Vektoren in einem komplexen Hilbert-Raum (reine Zustände) oder allgemein durch Dichteoperatoren (gemischte Zustände) dargestellt.5 Superpositionen, die durch reine Zustände dargestellt werden, werden verwendet, um Unsicherheiten zu modellieren, die noch nicht durch eine Messung aufgelöst wurden. Die Verwendung von Überlagerungen in der Biologie wird durch Abb. 1 veranschaulicht (siehe Abschnitt 10 und Artikel Khrennikov et al., 2018[12] für das entsprechende Modell). Das aus einer Beobachtung resultierende QP-Update basiert auf dem Projektionspostulat oder allgemeineren Transformationen von Quantenzuständen – im Rahmen der Theorie von Quanteninstrumenten (Davies und Lewis, 1970[16], Davies, 1976[17], Ozawa, 1984[18], Yuen, 1987[19], Ozawa , 1997[20], Ozawa, 2004[21], Okamura und Ozawa, 2016[22]) (Abschnitt 3).
Wir betonen, dass die quantenähnliche Modellierung die Rolle der Bequemlichkeit und Einfachheit der Quantendarstellung von Zuständen und Observablen erhöht. (Wir ignorieren pragmatisch das Problem der Wechselbeziehung von CP und QP.) Insbesondere hat der Quantenzustandsraum die lineare Struktur und lineare Modelle sind einfacher. Der Übergang von der klassischen nichtlinearen Dynamik elektrochemischer Prozesse in Biosystemen zur quantenlinearen Dynamik beschleunigt wesentlich die Zustandsentwicklung (Abschnitt 8.4). In diesem Rahmen ist „Zustand“ jedoch der Quanteninformationszustand eines Biosystems, der zur Verarbeitung spezieller Quantenunsicherheit verwendet wird (Abschnitt 8.2).
- ↑ Newton Isaac, «Philosophiae naturalis principia mathematica», Benjamin Motte, 1687, London UK».
- ↑ Kolmogorov A.N.Grundbegriffe Der Wahrscheinlichkeitsrechnung. Springer-Verlag, Berlin (1933)
- ↑ Penrose R. The Emperor’S New Mind Oxford Univ. Press, New-York (1989)
- ↑ Umezawa H. Advanced Field Theory: Micro, Macro and Thermal Concepts AIP, New York (1993)
- ↑ Hameroff S. Quantum coherence in microtubules. a neural basis for emergent con- sciousness? J. Cons. Stud., 1 (1994)
- ↑ Vitiello G. Dissipation and memory capacity in the quantum brain model Internat. J. Modern Phys. B, 9 (1995), p. 973
- ↑ Vitiello G. My Double Unveiled: The Dissipative Quantum Model of Brain, Advances in Consciousness Research, John Benjamins Publishing Company(2001)
- ↑ Arndt M., Juffmann T., Vedral V. Quantum physics meets biology HFSP J., 3 (6) (2009), pp. 386-400, 10.2976/1.3244985
- ↑ Bernroider G., Summhammer J. Can quantum entanglement between ion transition states effect action potential initiation? Cogn. Comput., 4 (2012), pp. 29-37
- ↑ Bernroider G. Neuroecology: Modeling neural systems and environments, from the quantum to the classical level and the question of consciousness J. Adv. Neurosci. Res., 4 (2017), pp. 1-9
- ↑ Plotnitsky A. Epistemology and Probability: Bohr, Heisenberg, SchrÖdinger and the Nature of Quantum-Theoretical Thinking Springer, Berlin, Germany; New York, NY, USA (2009
- ↑ Jump up to: 12.0 12.1 Khrennikov A., Basieva I., PothosE.M., Yamato I. Quantum Probability in Decision Making from Quantum Information Representation of Neuronal States, Sci. Rep., 8 (2018), Article 16225
- ↑ Khrennikov A. On quantum-like probabilistic structure of mental information Open Syst. Inf. Dyn., 11 (3) (2004), pp. 267-275
- ↑ Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Quantum information biology: from information interpretation of quantum mechanics to applications in molecular biology and cognitive psychology Found. Phys., 45 (10) (2015), pp. 1362-1378
- ↑ Kolmogorov A.N. Grundbegriffe Der Wahrscheinlichkeitsrechnung Springer-Verlag, Berlin (1933)
- ↑ Davies E.B., Lewis J.T. An operational approach to quantum probability Comm. Math. Phys., 17 (1970), pp. 239-260
- ↑ Davies E.B. Quantum Theory of Open Systems. Academic Press, London (1976)
- ↑ Ozawa M. Quantum measuring processes for continuous observables J. Math. Phys., 25 (1984), pp. 79-87
- ↑ Yuen, H. P., 1987. Characterization and realization of general quantum measurements. M. Namiki and others (ed.) Proc. 2nd Int. Symp. Foundations of Quantum Mechanics, pp. 360–363.
- ↑ Ozawa M. An operational approach to quantum state reduction Ann. Phys., NY, 259 (1997), pp. 121-137
- ↑ Ozawa M. Uncertainty relations for noise and disturbance in generalized quantum measurements Ann. Phys., NY, 311 (2004), pp. 350-416
- ↑ Okamura K., Ozawa M. Measurement theory in local quantum physics J. Math. Phys., 57 (2016), Article 015209