Difference between revisions of "Store:QLMen02"
Gianfranco (talk | contribs) (Created page with "== Introduction == The standard mathematical methods were originally developed to serve classical physics. The real analysis served as the mathematical basis of Newtonian mechanics (Newton, 1687)<ref>{{cita libro | autore = Newton Isaac | titolo = Philosophiae naturalis principia mathematica | url = https://archive.org/details/bub_gb_6EqxPav3vIsC | volume = | opera = | anno = 1687 | editore = Benjamin Motte | città = London UK | ISBN = | DOI = | PMID =...") |
Tags: Mobile web edit Mobile edit Visual edit |
||
| (9 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
== | == Introducción == | ||
Los métodos matemáticos estándar se desarrollaron originalmente para servir a la física clásica. El análisis real sirvió como base matemática de la mecánica newtoniana (Newton, 1687)<ref>Newton Isaac. Philosophiae naturalis principia mathematica.1687, Ed. Benjamin Motte, London UK</ref> (y posterior formalismo hamiltoniano); la mecánica estadística clásica estimuló el enfoque teórico de la medida de la teoría de la probabilidad, formalizado en la axiomática de Kolmogorov (Kolmogorov, 1933).<ref>Kolmogorov A.N.Grundbegriffe Der Wahrscheinlichkeitsrechnung. Springer-Verlag, Berlin (1933)</ref> Sin embargo, el comportamiento de los sistemas biológicos difiere esencialmente del comportamiento de los sistemas mecánicos, digamos cuerpos rígidos, moléculas de gas o fluidos. Por lo tanto, aunque las “matemáticas clásicas” aún desempeñan un papel crucial en el modelado biológico, parece que no pueden describir completamente la rica complejidad de los biosistemas y las peculiaridades de su comportamiento, en comparación con los sistemas mecánicos. Se están solicitando nuevos métodos matemáticos para modelar biosistemas.(a,b) | |||
En este artículo, presentamos las aplicaciones del formalismo matemático de la mecánica cuántica y su metodología para modelar el comportamiento de los biosistemas. (c) Los últimos años se caracterizaron por una explosión de interés por las aplicaciones de la teoría cuántica fuera de la física, especialmente en la psicología cognitiva. toma de decisiones, procesamiento de información en el cerebro, biología molecular, genética y epigenética, y teoría de la evolución.4 Llamamos a los modelos correspondientes de tipo cuántico. No están dirigidos al modelado a nivel micro de procesos físicos cuánticos reales en biosistemas, digamos en células o cerebros (cf. con aplicaciones biológicas de la teoría física cuántica genuina Penrose 1989<ref>Penrose R. The Emperor’S New Mind Oxford Univ. Press, New-York (1989)</ref>, Umezawa 1993<ref>Umezawa H. Advanced Field Theory: Micro, Macro and Thermal Concepts AIP, New York (1993)</ref>, Hameroff 1994<ref>Hameroff S. Quantum coherence in microtubules. a neural basis for emergent con- sciousness? J. Cons. Stud., 1 (1994)</ref>, Vitiello 1995<ref>Vitiello G. Dissipation and memory capacity in the quantum brain model Internat. J. Modern Phys. B, 9 (1995), p. 973</ref>, Vitiello 2001<ref>Vitiello G. My Double Unveiled: The Dissipative Quantum Model of Brain, Advances in Consciousness Research, John Benjamins Publishing Company(2001)</ref>, Arndt et al. al., 2009<ref>Arndt M., Juffmann T., Vedral V. Quantum physics meets biology HFSP J., 3 (6) (2009), pp. 386-400, 10.2976/1.3244985</ref>, Bernroider y Summhammer 2012<ref>Bernroider G., Summhammer J. Can quantum entanglement between ion transition states effect action potential initiation? Cogn. Comput., 4 (2012), pp. 29-37</ref>, Bernroider 2017<ref>Bernroider G. Neuroecology: Modeling neural systems and environments, from the quantum to the classical level and the question of consciousness J. Adv. Neurosci. Res., 4 (2017), pp. 1-9</ref>). El modelado de tipo cuántico funciona desde el punto de vista de la teoría cuántica como teoría de la medición. Este es el punto de vista original de Bohr que condujo a la interpretación de Copenhague de la mecánica cuántica (ver Plotnitsky, 2009<ref>Plotnitsky A. Epistemology and Probability: Bohr, Heisenberg, SchrÖdinger and the Nature of Quantum-Theoretical Thinking Springer, Berlin, Germany; New York, NY, USA (2009</ref> para una presentación clara y detallada de los puntos de vista de Bohr). Una de las principales bioespecialidades es la consideración de las automedidas que los biosistemas realizan sobre sí mismos. En nuestro modelo, la capacidad de realizar automedidas se considera la característica básica de las funciones biológicas (consulte la Sección 8.2 y el artículo Khrennikov et al., 2018<ref name=":Khrennikov A., Basieva I., PothosE.M., Yamato I.">Khrennikov A., Basieva I., PothosE.M., Yamato I. Quantum Probability in Decision Making from Quantum Information Representation of Neuronal States, Sci. Rep., 8 (2018), Article 16225</ref>). | |||
Modelos de tipo cuántico (Khrennikov, 2004b<ref name=":Khrennikov A. (2004)">Khrennikov A. On quantum-like probabilistic structure of mental information Open Syst. Inf. Dyn., 11 (3) (2004), pp. 267-275</ref>) | |||
reflejan las características de los procesos biológicos que coinciden naturalmente con el formalismo cuántico. En dicho modelado, es útil explorar la teoría de la información cuántica, que se puede aplicar no solo al micromundo de los sistemas cuánticos. Generalmente, los sistemas que procesan información de forma cuántica no necesitan ser sistemas físicos cuánticos; en particular, pueden ser biosistemas macroscópicos. Sorprendentemente, la misma teoría matemática se puede aplicar a todas las escalas biológicas: desde proteínas, células y cerebros hasta humanos y ecosistemas; podemos hablar de biología de la información cuántica (Asano et al., 2015a <ref name=":Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y., Yamato I.(2015a)">Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Quantum information biology: from information interpretation of quantum mechanics to applications in molecular biology and cognitive psychology Found. Phys., 45 (10) (2015), pp. 1362-1378</ref>). | |||
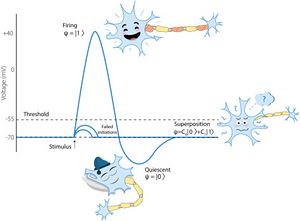
En el modelado de tipo cuántico, la teoría cuántica se considera como un cálculo para la predicción y transformación de probabilidades. El cálculo de probabilidad cuántica (QP) (Sección 2) difiere esencialmente del cálculo de probabilidad clásico (CP) basado en la axiomática de Kolmogorov (Kolmogorov, 1933<ref name=":2">Kolmogorov A.N. Grundbegriffe Der Wahrscheinlichkeitsrechnung Springer-Verlag, Berlin (1933)</ref>).En CP, los estados de los sistemas aleatorios están representados por medidas de probabilidad y los observables por variables aleatorias; en QP, los estados de los sistemas aleatorios se representan mediante vectores normalizados en un espacio de Hilbert complejo (estados puros) o, en general, mediante operadores de densidad (estados mixtos).5 Las superposiciones representadas por estados puros se utilizan para modelar la incertidumbre que aún no ha sido resuelta por una medición. El uso de superposiciones en biología se ilustra en la Fig. 1 (consulte la Sección 10 y el artículo Khrennikov et al., 2018) <ref name=":Khrennikov A., Basieva I., Pothos E.M., Yamato I.(2018)"> Khrennikov A., Basieva I., Pothos E.M., Yamato I.> Quantum Probability in Decision Making from Quantum Information Representation of Neuronal States, Sci. Rep., 8 (2018), Article 16225 </ref> | |||
para el modelo correspondiente). La actualización QP resultante de una observación se basa en el postulado de proyección o transformaciones más generales de estados cuánticos — en el marco de la teoría de instrumentos cuánticos (Davies y Lewis, 1970<ref name=":3">Davies E.B., Lewis J.T. An operational approach to quantum probability Comm. Math. Phys., 17 (1970), pp. 239-260</ref>, Davies, 1976<ref name=":4">Davies E.B. Quantum Theory of Open Systems. Academic Press, London (1976)</ref>, Ozawa, 1984<ref name=":5">Ozawa M. Quantum measuring processes for continuous observables J. Math. Phys., 25 (1984), pp. 79-87</ref>, Yuen, 1987<ref name=":6">Yuen, H. P., 1987. Characterization and realization of general quantum measurements. M. Namiki and others (ed.) Proc. 2nd Int. Symp. Foundations of Quantum Mechanics, pp. 360–363.</ref>, Ozawa , 1997<ref name=":7">Ozawa M. An operational approach to quantum state reduction Ann. Phys., NY, 259 (1997), pp. 121-137</ref>, Ozawa, 2004<ref name=":Ozawa M. Uncertainty ">Ozawa M. Uncertainty relations for noise and disturbance in generalized quantum measurements Ann. Phys., NY, 311 (2004), pp. 350-416</ref>, Okamura y Ozawa, 2016<ref name=":9">Okamura K., Ozawa M. Measurement theory in local quantum physics J. Math. Phys., 57 (2016), Article 015209</ref>) (Sección 3). | |||
[[File:Schrodinger 1.jpeg|left|thumb|Fig. 1. Illustration for quantum-like representation of uncertainty generated by neuron’s action potential (originally published in Khrennikov et al. (2018)).]] | [[File:Schrodinger 1.jpeg|left|thumb|Fig. 1. Illustration for quantum-like representation of uncertainty generated by neuron’s action potential (originally published in Khrennikov et al. (2018)).]] | ||
Hacemos hincapié en que el modelado de tipo cuántico eleva el papel de la conveniencia y la simplicidad de la representación cuántica de estados y observables. (Ignoramos pragmáticamente el problema de la interrelación de CP y QP). En particular, el espacio de estado cuántico tiene una estructura lineal y los modelos lineales son más simples. La transición de la dinámica no lineal clásica de los procesos electroquímicos en biosistemas a la dinámica lineal cuántica esencialmente acelera la evolución del estado (Sección 8.4). Sin embargo, en este marco, "estado" es el estado de información cuántica de un biosistema utilizado para el procesamiento de la incertidumbre cuántica especial (Sección 8.2). | |||
Latest revision as of 18:10, 16 April 2023
Introducción
Los métodos matemáticos estándar se desarrollaron originalmente para servir a la física clásica. El análisis real sirvió como base matemática de la mecánica newtoniana (Newton, 1687)[1] (y posterior formalismo hamiltoniano); la mecánica estadística clásica estimuló el enfoque teórico de la medida de la teoría de la probabilidad, formalizado en la axiomática de Kolmogorov (Kolmogorov, 1933).[2] Sin embargo, el comportamiento de los sistemas biológicos difiere esencialmente del comportamiento de los sistemas mecánicos, digamos cuerpos rígidos, moléculas de gas o fluidos. Por lo tanto, aunque las “matemáticas clásicas” aún desempeñan un papel crucial en el modelado biológico, parece que no pueden describir completamente la rica complejidad de los biosistemas y las peculiaridades de su comportamiento, en comparación con los sistemas mecánicos. Se están solicitando nuevos métodos matemáticos para modelar biosistemas.(a,b)
En este artículo, presentamos las aplicaciones del formalismo matemático de la mecánica cuántica y su metodología para modelar el comportamiento de los biosistemas. (c) Los últimos años se caracterizaron por una explosión de interés por las aplicaciones de la teoría cuántica fuera de la física, especialmente en la psicología cognitiva. toma de decisiones, procesamiento de información en el cerebro, biología molecular, genética y epigenética, y teoría de la evolución.4 Llamamos a los modelos correspondientes de tipo cuántico. No están dirigidos al modelado a nivel micro de procesos físicos cuánticos reales en biosistemas, digamos en células o cerebros (cf. con aplicaciones biológicas de la teoría física cuántica genuina Penrose 1989[3], Umezawa 1993[4], Hameroff 1994[5], Vitiello 1995[6], Vitiello 2001[7], Arndt et al. al., 2009[8], Bernroider y Summhammer 2012[9], Bernroider 2017[10]). El modelado de tipo cuántico funciona desde el punto de vista de la teoría cuántica como teoría de la medición. Este es el punto de vista original de Bohr que condujo a la interpretación de Copenhague de la mecánica cuántica (ver Plotnitsky, 2009[11] para una presentación clara y detallada de los puntos de vista de Bohr). Una de las principales bioespecialidades es la consideración de las automedidas que los biosistemas realizan sobre sí mismos. En nuestro modelo, la capacidad de realizar automedidas se considera la característica básica de las funciones biológicas (consulte la Sección 8.2 y el artículo Khrennikov et al., 2018[12]).
Modelos de tipo cuántico (Khrennikov, 2004b[13])
reflejan las características de los procesos biológicos que coinciden naturalmente con el formalismo cuántico. En dicho modelado, es útil explorar la teoría de la información cuántica, que se puede aplicar no solo al micromundo de los sistemas cuánticos. Generalmente, los sistemas que procesan información de forma cuántica no necesitan ser sistemas físicos cuánticos; en particular, pueden ser biosistemas macroscópicos. Sorprendentemente, la misma teoría matemática se puede aplicar a todas las escalas biológicas: desde proteínas, células y cerebros hasta humanos y ecosistemas; podemos hablar de biología de la información cuántica (Asano et al., 2015a [14]).
En el modelado de tipo cuántico, la teoría cuántica se considera como un cálculo para la predicción y transformación de probabilidades. El cálculo de probabilidad cuántica (QP) (Sección 2) difiere esencialmente del cálculo de probabilidad clásico (CP) basado en la axiomática de Kolmogorov (Kolmogorov, 1933[15]).En CP, los estados de los sistemas aleatorios están representados por medidas de probabilidad y los observables por variables aleatorias; en QP, los estados de los sistemas aleatorios se representan mediante vectores normalizados en un espacio de Hilbert complejo (estados puros) o, en general, mediante operadores de densidad (estados mixtos).5 Las superposiciones representadas por estados puros se utilizan para modelar la incertidumbre que aún no ha sido resuelta por una medición. El uso de superposiciones en biología se ilustra en la Fig. 1 (consulte la Sección 10 y el artículo Khrennikov et al., 2018) [16]
para el modelo correspondiente). La actualización QP resultante de una observación se basa en el postulado de proyección o transformaciones más generales de estados cuánticos — en el marco de la teoría de instrumentos cuánticos (Davies y Lewis, 1970[17], Davies, 1976[18], Ozawa, 1984[19], Yuen, 1987[20], Ozawa , 1997[21], Ozawa, 2004[22], Okamura y Ozawa, 2016[23]) (Sección 3).
Hacemos hincapié en que el modelado de tipo cuántico eleva el papel de la conveniencia y la simplicidad de la representación cuántica de estados y observables. (Ignoramos pragmáticamente el problema de la interrelación de CP y QP). En particular, el espacio de estado cuántico tiene una estructura lineal y los modelos lineales son más simples. La transición de la dinámica no lineal clásica de los procesos electroquímicos en biosistemas a la dinámica lineal cuántica esencialmente acelera la evolución del estado (Sección 8.4). Sin embargo, en este marco, "estado" es el estado de información cuántica de un biosistema utilizado para el procesamiento de la incertidumbre cuántica especial (Sección 8.2).
- ↑ Newton Isaac. Philosophiae naturalis principia mathematica.1687, Ed. Benjamin Motte, London UK
- ↑ Kolmogorov A.N.Grundbegriffe Der Wahrscheinlichkeitsrechnung. Springer-Verlag, Berlin (1933)
- ↑ Penrose R. The Emperor’S New Mind Oxford Univ. Press, New-York (1989)
- ↑ Umezawa H. Advanced Field Theory: Micro, Macro and Thermal Concepts AIP, New York (1993)
- ↑ Hameroff S. Quantum coherence in microtubules. a neural basis for emergent con- sciousness? J. Cons. Stud., 1 (1994)
- ↑ Vitiello G. Dissipation and memory capacity in the quantum brain model Internat. J. Modern Phys. B, 9 (1995), p. 973
- ↑ Vitiello G. My Double Unveiled: The Dissipative Quantum Model of Brain, Advances in Consciousness Research, John Benjamins Publishing Company(2001)
- ↑ Arndt M., Juffmann T., Vedral V. Quantum physics meets biology HFSP J., 3 (6) (2009), pp. 386-400, 10.2976/1.3244985
- ↑ Bernroider G., Summhammer J. Can quantum entanglement between ion transition states effect action potential initiation? Cogn. Comput., 4 (2012), pp. 29-37
- ↑ Bernroider G. Neuroecology: Modeling neural systems and environments, from the quantum to the classical level and the question of consciousness J. Adv. Neurosci. Res., 4 (2017), pp. 1-9
- ↑ Plotnitsky A. Epistemology and Probability: Bohr, Heisenberg, SchrÖdinger and the Nature of Quantum-Theoretical Thinking Springer, Berlin, Germany; New York, NY, USA (2009
- ↑ Khrennikov A., Basieva I., PothosE.M., Yamato I. Quantum Probability in Decision Making from Quantum Information Representation of Neuronal States, Sci. Rep., 8 (2018), Article 16225
- ↑ Khrennikov A. On quantum-like probabilistic structure of mental information Open Syst. Inf. Dyn., 11 (3) (2004), pp. 267-275
- ↑ Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Quantum information biology: from information interpretation of quantum mechanics to applications in molecular biology and cognitive psychology Found. Phys., 45 (10) (2015), pp. 1362-1378
- ↑ Kolmogorov A.N. Grundbegriffe Der Wahrscheinlichkeitsrechnung Springer-Verlag, Berlin (1933)
- ↑ Khrennikov A., Basieva I., Pothos E.M., Yamato I.> Quantum Probability in Decision Making from Quantum Information Representation of Neuronal States, Sci. Rep., 8 (2018), Article 16225
- ↑ Davies E.B., Lewis J.T. An operational approach to quantum probability Comm. Math. Phys., 17 (1970), pp. 239-260
- ↑ Davies E.B. Quantum Theory of Open Systems. Academic Press, London (1976)
- ↑ Ozawa M. Quantum measuring processes for continuous observables J. Math. Phys., 25 (1984), pp. 79-87
- ↑ Yuen, H. P., 1987. Characterization and realization of general quantum measurements. M. Namiki and others (ed.) Proc. 2nd Int. Symp. Foundations of Quantum Mechanics, pp. 360–363.
- ↑ Ozawa M. An operational approach to quantum state reduction Ann. Phys., NY, 259 (1997), pp. 121-137
- ↑ Ozawa M. Uncertainty relations for noise and disturbance in generalized quantum measurements Ann. Phys., NY, 311 (2004), pp. 350-416
- ↑ Okamura K., Ozawa M. Measurement theory in local quantum physics J. Math. Phys., 57 (2016), Article 015209