Difference between revisions of "Store:EEMIit08"
Gianfranco (talk | contribs) (Created page with "=== Table 2=== {| class="wikitable" !Stimulus !<math>\Delta x\Delta p_x</math> !<math>\Delta y\Delta p_y</math> !<math>\Delta x\Delta p_x</math> !<math>\Delta y\Delta p_y</math> !<math>\Delta x\Delta p_x</math> !<math>\Delta y\Delta p_y</math> !<math>\Delta x\Delta p_x</math> !<math>\Delta y\Delta p_y</math> |- | colspan="1" rowspan="1" |Taken | colspan="1" rowspan="1" |<small><math display="inline">(7\pm2.1)10^{-1}</math></small> | colspan="1" rowspan="1" |<small><math...") |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
=== | === Tabella 2=== | ||
{| class="wikitable" | {| class="wikitable" | ||
! | |+Vari valori estratti dall'andamento temporale dei prodotti <math>\Delta x(t)\Delta p_x(t)</math> e <math>\Delta y(t)\Delta p_y(t)</math>. | ||
!Stimolo | |||
!<math>\Delta x\Delta p_x</math> | !<math>\Delta x\Delta p_x</math> | ||
!<math>\Delta y\Delta p_y</math> | !<math>\Delta y\Delta p_y</math> | ||
| Line 12: | Line 13: | ||
!<math>\Delta y\Delta p_y</math> | !<math>\Delta y\Delta p_y</math> | ||
|- | |- | ||
| colspan="1" rowspan="1" |Taken | | colspan="1" rowspan="1" |Taken | ||
| colspan="1" rowspan="1" |<small><math display="inline">(7\pm2.1)10^{-1}</math></small> | | colspan="1" rowspan="1" |<small><math display="inline">(7\pm2.1)10^{-1}</math></small> | ||
| colspan="1" rowspan="1" |<small><math display="inline">(7.2\pm1.8)10^{-1}</math></small> | | colspan="1" rowspan="1" |<small><math display="inline">(7.2\pm1.8)10^{-1}</math></small> | ||
| Line 22: | Line 23: | ||
| colspan="1" rowspan="1" |<small><math display="inline">(1.3\pm0.4)10^{1}</math></small> | | colspan="1" rowspan="1" |<small><math display="inline">(1.3\pm0.4)10^{1}</math></small> | ||
|- | |- | ||
| colspan="1" rowspan="1" |Taken | | colspan="1" rowspan="1" |Taken Destrutturato | ||
| colspan="1" rowspan="1" |<small><math display="inline">(6.4\pm2.6)10^{-1}</math></small> | | colspan="1" rowspan="1" |<small><math display="inline">(6.4\pm2.6)10^{-1}</math></small> | ||
| colspan="1" rowspan="1" |<small><math display="inline">(6.8\pm2.1)10^{-1}</math></small> | | colspan="1" rowspan="1" |<small><math display="inline">(6.8\pm2.1)10^{-1}</math></small> | ||
| Line 32: | Line 33: | ||
| colspan="1" rowspan="1" |<small><math display="inline">(1.4\pm0.7)10^{1}</math></small> | | colspan="1" rowspan="1" |<small><math display="inline">(1.4\pm0.7)10^{1}</math></small> | ||
|- | |- | ||
| colspan="1" rowspan="1" |Bang! | | colspan="1" rowspan="1" |Bang! tu sei morto (BYD) | ||
| colspan="1" rowspan="1" |<small><math display="inline">(7.6\pm4.9)10^{-1}</math></small> | | colspan="1" rowspan="1" |<small><math display="inline">(7.6\pm4.9)10^{-1}</math></small> | ||
| colspan="1" rowspan="1" |<small><math display="inline">(7.5\pm3.1)10^{-1}</math></small> | | colspan="1" rowspan="1" |<small><math display="inline">(7.5\pm3.1)10^{-1}</math></small> | ||
| Line 42: | Line 43: | ||
| colspan="1" rowspan="1" |<small><math display="inline">(2.7\pm3.9)10^{1}</math></small> | | colspan="1" rowspan="1" |<small><math display="inline">(2.7\pm3.9)10^{1}</math></small> | ||
|- | |- | ||
|colspan="1" rowspan="1" |Bang! | | colspan="1" rowspan="1" |Bang! tu sei morto (BYD) | ||
Destrutturato | |||
| colspan="1" rowspan="1" |<small><math display="inline">(7.4\pm3.2)10^{-1}</math></small> | | colspan="1" rowspan="1" |<small><math display="inline">(7.4\pm3.2)10^{-1}</math></small> | ||
| colspan="1" rowspan="1" |<small><math display="inline">(7.1\pm2.9)10^{-1}</math></small> | | colspan="1" rowspan="1" |<small><math display="inline">(7.1\pm2.9)10^{-1}</math></small> | ||
| Line 52: | Line 54: | ||
| colspan="1" rowspan="1" |<small><math display="inline">(1.5\pm0.8)10^{1}</math></small> | | colspan="1" rowspan="1" |<small><math display="inline">(1.5\pm0.8)10^{1}</math></small> | ||
|- | |- | ||
|colspan="1" rowspan="1" |Rest (Pre-Taken) | | colspan="1" rowspan="1" |Rest (Pre-Taken) | ||
| colspan="1" rowspan="1" |<small><math display="inline">(9.7\pm4.2)10^{-1}</math></small> | | colspan="1" rowspan="1" |<small><math display="inline">(9.7\pm4.2)10^{-1}</math></small> | ||
| colspan="1" rowspan="1" |<small><math display="inline">(1.1\pm0.6)10^{0}</math></small> | | colspan="1" rowspan="1" |<small><math display="inline">(1.1\pm0.6)10^{0}</math></small> | ||
| Line 72: | Line 74: | ||
| colspan="1" rowspan="1" |<small><math display="inline">(1.9\pm0.8)10^{1}</math></small> | | colspan="1" rowspan="1" |<small><math display="inline">(1.9\pm0.8)10^{1}</math></small> | ||
|} | |} | ||
[[File:Figure 3.jpeg|center|thumb|788px|<small>'''Figura 3:''' | |||
Considerando il valore minimo che questi prodotti raggiungono per ogni soggetto, vediamo un valore costante sia in x che in y di <math>0,78\pm0,41\tfrac{cm^2}{4ms}</math>, un valore medio di <math>9,3\pm4,4\tfrac{cm^2}{4ms}</math> e una deviazione standard costante di <math>18\pm29\tfrac{cm^2}{4ms}</math>. L'unità di <math>\tfrac{cm^2}{4ms}</math> deriva dal campionamento di 250 Hz. I valori massimi differiscono a seconda della stimolazione. I valori sono riportati come media tra soggetti più o meno 1 deviazione standard. | |||
[[File:Figure 3.jpeg|center|thumb|788px|<small>'''Figura 3:''' Mappe di probabilità corrispondenti al punto temporale meno incerto per ciascuna delle sei condizioni sperimentali. '''(A)''' Le probabilità che portano all'incertezza minima definita dal minimo di . (B) Le probabilità che portano all'incertezza minima definita dal minimo di <math>\Delta x(t)\Delta p_x(t)</math>. '''(B)''' Le probabilità che portano all'incertezza minima definita dal minimo di <math>\Delta y(t)\Delta p_y(t)</math>.Viene visualizzato un soggetto per tutti gli stimoli Taken ed un altro per tutti gli stimoli Bang! Sei morto.</small>]] | |||
Latest revision as of 09:47, 30 March 2023
Tabella 2
| Stimolo | ||||||||
|---|---|---|---|---|---|---|---|---|
| Taken | ||||||||
| Taken Destrutturato | ||||||||
| Bang! tu sei morto (BYD) | ||||||||
| Bang! tu sei morto (BYD)
Destrutturato |
||||||||
| Rest (Pre-Taken) | ||||||||
| Rest (Pre-BYD) |
Considerando il valore minimo che questi prodotti raggiungono per ogni soggetto, vediamo un valore costante sia in x che in y di , un valore medio di e una deviazione standard costante di . L'unità di deriva dal campionamento di 250 Hz. I valori massimi differiscono a seconda della stimolazione. I valori sono riportati come media tra soggetti più o meno 1 deviazione standard.
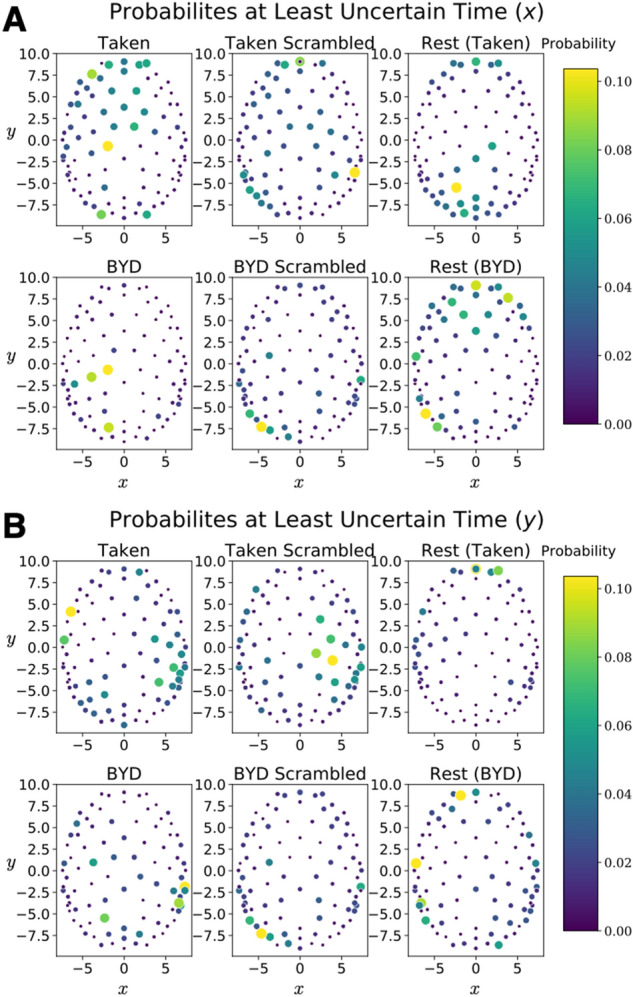
Figura 3: Mappe di probabilità corrispondenti al punto temporale meno incerto per ciascuna delle sei condizioni sperimentali. (A) Le probabilità che portano all'incertezza minima definita dal minimo di . (B) Le probabilità che portano all'incertezza minima definita dal minimo di . (B) Le probabilità che portano all'incertezza minima definita dal minimo di .Viene visualizzato un soggetto per tutti gli stimoli Taken ed un altro per tutti gli stimoli Bang! Sei morto.



















































