Difference between revisions of "Store:LPLit04"
Gianfranco (talk | contribs) (Created page with "==Probabilistic-causal analysis== From these premises it is clear that the clinical diagnosis is made using the so-called hypothetical-deductive method referred to as DN<ref name=":1">{{Cite book | autore = Sarkar S | titolo = Nagel on Reduction | url = https://pubmed.ncbi.nlm.nih.gov/26386529/ | volume = | opera = Stud Hist Philos Sci | anno = 2015 | editore = | città = | ISBN = | PMID = 26386529 | PMCID = | DOI = 10.1016/j.shpsa.2015.05.006 | oaf...") |
|||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Analisi probabilistico-causale == | |||
=== | Dalle premesse emerge che la diagnosi clinica viene effettuata tramite il metodo ipotetico-deduttivo, noto come DN<ref name=":1">{{Cite book | autore = Sarkar S | titolo = Nagel on Reduction | url = https://pubmed.ncbi.nlm.nih.gov/26386529/ | volume = | opera = Stud Hist Philos Sci | anno = 2015 | editore = | città = | ISBN = | PMID = 26386529 | PMCID = | DOI = 10.1016/j.shpsa.2015.05.006 | oaf = <!-- qualsiasi valore --> | LCCN = | OCLC = }}</ref> (modello deduttivo-nomologico)<ref>''DN model of scientific explanation'', also known as ''Hempel's model'', ''Hempel–Oppenheim model'', ''Popper–Hempel model'', or ''covering law model''</ref>. Tuttavia, questa rappresentazione non è realistica, in quanto le conoscenze mediche impiegate nel processo decisionale clinico raramente includono leggi deterministiche causali che consentono spiegazioni causali e, di conseguenza, la formulazione di diagnosi cliniche, soprattutto in ambito specialistico. Esaminiamo nuovamente il caso di Mary Poppins, tentando questa volta un approccio probabilistico-causale. | ||
Prendiamo in considerazione un gruppo di <math>n</math> individui, inclusi quelli che lamentano dolore orofacciale generalmente associato a degenerazione ossea dell'articolazione temporo-mandibolare. Tuttavia, potrebbero esistere altre cause apparentemente non correlate. È necessario tradurre matematicamente la "rilevanza" che queste incertezze causali rivestono nel determinare una diagnosi. | |||
---- | |||
=== La rilevanza causale === | |||
Per affrontare questa questione, consideriamo il grado di rilevanza causale <math>(cr)</math> di un evento <math>E_1</math> rispetto a un evento <math>E_2</math>, dove: | |||
* <math>E_1</math> = pazienti con degenerazione ossea dell'articolazione temporo-mandibolare. | |||
* <math>E_2</math> = pazienti che hanno riportato dolore orofacciale. | |||
* <math>E_3</math> = pazienti senza degenerazione ossea dell'articolazione temporo-mandibolare. | |||
<math> | La probabilità condizionata <math>P(A \mid B)</math> è usata per calcolare la probabilità che l'evento <math>A</math> si verifichi dato che l'evento <math>B</math> si è già verificato. | ||
La rilevanza causale <math>cr</math> del campione <math>E_1</math> di pazienti si determina come: | |||
<math>cr = P(E_2 \mid E_1) - P(E_2 \mid E_3)</math> | |||
dove: | |||
<blockquote><math>P(E_2 \mid E_1)</math> indica la probabilità che alcune persone (tra <math>n</math> considerate) soffrano di dolore orofacciale causato dalla degenerazione ossea dell'articolazione temporo-mandibolare,</blockquote> | |||
mentre | |||
<blockquote><math>P(E_2 \mid E_3)</math> indica la probabilità che altre persone (sempre tra <math>n</math> considerate) soffrano di dolore orofacciale causato da altri fattori non legati alla degenerazione ossea dell'articolazione temporo-mandibolare.</blockquote> | |||
Poiché tutte le probabilità suggeriscono che <math>P(A \mid B)</math>, il valore di <math>cr</math> sarà compreso tra <math>-1</math> e <math>1</math>. | |||
I significati attribuibili a questo valore sono: | |||
<blockquote><math>cr = 1</math> indica che l'unica causa di dolore orofacciale è la degenerazione ossea dell'ATM,</blockquote> | |||
<blockquote><math>cr = -1</math> indica che la degenerazione ossea dell'ATM non è mai la causa del dolore orofacciale, ma sempre qualcos'altro,</blockquote> | |||
<blockquote><math>cr = 0</math> indica che la probabilità che il dolore orofacciale sia causato dalla degenerazione ossea dell'ATM o da altri fattori è esattamente la stessa,</blockquote> | |||
e, nei casi intermedi, più realistici: | |||
<blockquote><math>cr > 0</math> indica che è più probabile che la degenerazione ossea dell'ATM sia la causa del dolore orofacciale,</blockquote> | |||
<blockquote><math>cr < 0</math> indica che è più probabile che la causa del dolore orofacciale non sia la degenerazione ossea dell'ATM.</blockquote> | |||
---- | |||
<center> | |||
---- | |||
===2° Approccio clinico === | |||
<gallery widths="350" heights="282" perrow="2" mode="slideshow"> | <gallery widths="350" heights="282" perrow="2" mode="slideshow"> | ||
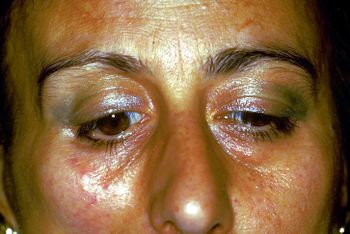
File:Spasmo emimasticatorio.jpg|''' | File:Spasmo emimasticatorio.jpg|'''Figura 1:''' Paziente che riferisce "Dolore orofacciale emilaterale destro" | ||
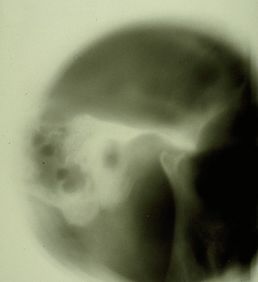
File:Spasmo emimasticatorio ATM.jpg|''' | File:Spasmo emimasticatorio ATM.jpg|'''Figura 2:''' Stratigrafia dell'ATM del paziente che mostra segni di appiattimento condilare e osteofiti | ||
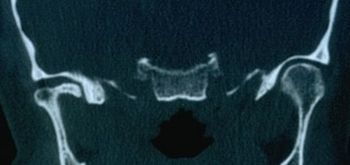
File:Atm1 sclerodermia.jpg|''' | File:Atm1 sclerodermia.jpg|'''Figura 3:''' Tomografia computerizzata dell'ATM | ||
File:Spasmo emimasticatorio assiografia.jpg|''' | File:Spasmo emimasticatorio assiografia.jpg|'''Figura 4:''' Assiografia del paziente che mostra un appiattimento del pattern masticatorio sul condilo destro | ||
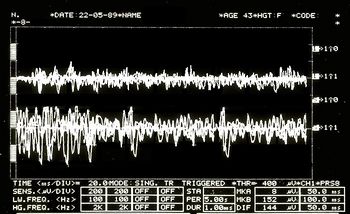
File:EMG2.jpg|''' | File:EMG2.jpg|'''Figura 5:''' Schema interferente EMG. Tracce superiori sovrapposte corrispondenti al massetere destro, in basso al massetere sinistro. | ||
</gallery> | </gallery> | ||
</center> | </center> | ||
Sia quindi <math>P(D)</math> la probabilità di identificare, nel nostro campione di <math>n</math> persone, individui che presentano gli elementi appartenenti all'insieme specificato <math>D={\delta_1,\delta_2,...,\delta_n}</math>. Per utilizzare le informazioni fornite da questo dataset, viene introdotto il concetto di partizione di rilevanza causale: | |||
==== La partizione della rilevanza causale ==== | |||
Essendo <math>n</math> il numero di persone su cui dobbiamo condurre le analisi, se dividiamo questo gruppo, in base a determinate condizioni come spiegato di seguito, in <math>k</math> sottoinsiemi <math>C_i</math> con <math>i=1,2,\dots,k</math>, viene creato un cluster chiamato "set di partizioni" <math>\pi</math>. | |||
<math>\pi = {C_1, C_2,\dots,C_k } \qquad \qquad \text{con} \qquad \qquad C_i \subset n ,</math> | |||
dove il simbolismo <math>C_i \subset n</math> indica che la sottoclasse <math>C_i</math> è contenuta nel numero <math>n</math>. | |||
Per poter definire la partizione <math>\pi</math> come partizione di rilevanza causale, deve possedere queste proprietà: <blockquote>Per ogni sottoclasse <math>C_i</math>, la condizione deve essere che <math>rc=P(D \mid C_i)- P(D) \neq 0,</math> ovvero la probabilità di trovare nel sottogruppo <math>C_i</math> una persona che presenti i sintomi, i segni clinici e gli elementi appartenenti all'insieme <math>D={\delta_1,\delta_2,...,\delta_n}</math>. Una partizione causalmente rilevante di questo tipo viene definita '''omogenea'''. | |||
Ogni sottoinsieme <math>C_i</math> deve essere 'elementare', cioè non deve essere ulteriormente suddiviso in altri sottoinsiemi, poiché, in tal caso, non avrebbero rilevanza causale.</blockquote> Assumiamo ora, ad esempio, che il campione di popolazione <math>n</math>, a cui appartiene la nostra paziente Mary Poppins, sia una categoria di soggetti dai 20 ai 70 anni. Supponiamo inoltre che in questa popolazione ci siano individui che presentano gli elementi appartenenti al set di dati <math>D={\delta_1,.....,\delta_n}</math>, corrispondenti alle prove di laboratorio menzionate e descritte in '[[La logica del linguaggio classico]]'. | |||
Supponiamo che in un campione di 10.000 soggetti dai 20 ai 70 anni abbiamo un'incidenza di 30 soggetti <math>p(D)=0.003</math> che presentano i segni clinici <math>\delta_1</math> e <math>\delta_4</math>. Abbiamo scelto di utilizzare questi dati per dimostrare il processo probabilistico perché in letteratura i dati relativi ai segni e sintomi clinici per i disturbi temporo-mandibolari variano ampiamente e presentano un'incidenza che riteniamo eccessivamente alta. | |||
<ref name=":2">{{Cite book | |||
| autore = Pantoja LLQ | | autore = Pantoja LLQ | ||
| autore2 = De Toledo IP | | autore2 = De Toledo IP | ||
| Line 208: | Line 187: | ||
}}</ref> | }}</ref> | ||
Un esempio di una partizione con presunta probabilità in cui la degenerazione dell'ATM (Deg.TMJ) si verifica in combinazione con i disturbi temporomandibolari (TMD) sarebbe il seguente: | |||
{| | {| | ||
|+ | |+ | ||
|<math>P(D| Deg.TMJ \cap TMDs)=0.95 \qquad \qquad \; </math> | |<math>P(D| Deg.TMJ \cap TMDs)=0.95 \qquad \qquad \; </math> | ||
| | | | ||
| | |dove | ||
| | | | ||
| | | | ||
| Line 220: | Line 200: | ||
|<math>P(D| Deg.TMJ \cap noTMDs)=0.3 \qquad \qquad \quad </math> | |<math>P(D| Deg.TMJ \cap noTMDs)=0.3 \qquad \qquad \quad </math> | ||
| | | | ||
| | |dove | ||
| | | | ||
| | | | ||
| Line 227: | Line 207: | ||
|<math>P(D| no Deg.TMJ \cap TMDs)=0.199 \qquad \qquad \; </math> | |<math>P(D| no Deg.TMJ \cap TMDs)=0.199 \qquad \qquad \; </math> | ||
| | | | ||
| | |dove | ||
| | | | ||
| | | | ||
| Line 234: | Line 214: | ||
|<math>P(D| noDeg.TMJ \cap noTMDs)=0.001 \qquad \qquad \;</math> | |<math>P(D| noDeg.TMJ \cap noTMDs)=0.001 \qquad \qquad \;</math> | ||
| | | | ||
| | |dove | ||
| | | | ||
| | | | ||
|<math> C_4\equiv noDeg.TMJ \cap noTMDs</math> | |<math> C_4\equiv noDeg.TMJ \cap noTMDs</math> | ||
|} | |} | ||
{{q2|Una partizione omogenea fornisce ciò che siamo abituati a chiamare Diagnosi Differenziale.|}} | |||
==== Situazioni cliniche ==== | |||
Queste probabilità condizionali dimostrano che ciascuna delle quattro sottoclassi della partizione è causalmente rilevante per i dati del paziente <math>D={\delta_1,.....\delta_n}</math> nel campione di popolazione <math>PO</math>. Date le suddette partizioni della classe di riferimento, abbiamo le seguenti situazioni cliniche: | |||
* <math>\mathbb{C}_1 \equiv</math> Mary Poppins <math>\in</math> degenerazione dell'articolazione temporo-mandibolare <math>\cap</math> Disturbi temporo-mandibolari | |||
* <math>\mathbb{C}_2 \equiv</math> Mary Poppins <math>\in</math> degenerazione dell'articolazione temporo-mandibolare <math>\cap</math> no Disturbi temporo-mandibolari | |||
*Mary Poppins <math>\in</math> | * <math>\mathbb{C}_3 \equiv</math> Mary Poppins <math>\in</math> no degenerazione dell'articolazione temporo-mandibolare <math>\cap</math> Disturbi temporo-mandibolari | ||
* <math>\mathbb{C}_4 \equiv</math> Mary Poppins <math>\in</math> no degenerazione dell'articolazione temporo-mandibolare <math>\cap</math> no Disturbi temporo-mandibolari Per arrivare alla diagnosi finale sopra menzionata, abbiamo condotto un'analisi probabilistico-causale dello stato di salute di Mary Poppins, i cui dati iniziali erano <math>D={\delta_1,.....\delta_n}</math>. | |||
In generale, possiamo fare riferimento a un processo logico in cui esaminiamo i seguenti elementi: | |||
* | * Un individuo: <math>a</math> | ||
* Il suo set di dati iniziale <math>D={\delta_1,.....\delta_n}</math> | |||
* Un campione di popolazione <math>n</math> a cui appartiene | |||
* Una probabilità di base <math>P(D)=0.003</math> | |||
A questo punto, dovremmo introdurre argomentazioni troppo specialistiche che distoglierebbero il lettore dall'argomento principale, ma che hanno un'elevata importanza epistemica. Pertanto, cercheremo di estrarre il filo logico più semplice descritto nel concetto Analysandum/Analysans. | |||
Nell'analisi probabilistico-causale di <math>D={\delta_1,.....\delta_n}</math>, si distinguono un paio delle seguenti forme logiche (Analysandum/Analysans): | |||
*'''Analysan <math>= \{\pi,a,KB\}</math> | <blockquote> | ||
* '''Analysandum''' <math>= \{P(D),a\}</math>: è una forma logica che contiene due parametri: la probabilità <math>P(D)</math> di selezionare una persona che presenta i sintomi e gli elementi appartenenti all'insieme <math>D=\{\delta_1,\delta_2,...,\delta_n\}</math> e il generico individuo <math>a</math> incline a quei sintomi. | |||
* '''Analysan''' <math>= \{\pi, a, KB\}</math>: è una forma logica che contiene tre parametri: la partizione <math>\pi</math>, il generico individuo <math>a</math> appartenente al campione di popolazione <math>n</math> e la <math>KB</math> (Conoscenza di base), che comprende un insieme di affermazioni di probabilità condizionata superiori a <math>n>1</math>. | |||
</blockquote> | |||
Ad esempio, si può concludere che la diagnosi definitiva sia la seguente: | |||
<math>P(D|Deg.TMJ \cap TMDs)=0.95</math> | |||
significa che la nostra Mary Poppins ha il 95% di probabilità di soffrire di Disturbi Temporo-Mandibolari (TMD), in quanto presenta una degenerazione dell'articolazione temporo-mandibolare oltre ad altri indicatori positivi inclusi nel set di dati <math>D={\delta_1,.....\delta_n}</math>. | |||
Latest revision as of 12:20, 29 March 2024
Analisi probabilistico-causale
Dalle premesse emerge che la diagnosi clinica viene effettuata tramite il metodo ipotetico-deduttivo, noto come DN[1] (modello deduttivo-nomologico)[2]. Tuttavia, questa rappresentazione non è realistica, in quanto le conoscenze mediche impiegate nel processo decisionale clinico raramente includono leggi deterministiche causali che consentono spiegazioni causali e, di conseguenza, la formulazione di diagnosi cliniche, soprattutto in ambito specialistico. Esaminiamo nuovamente il caso di Mary Poppins, tentando questa volta un approccio probabilistico-causale.
Prendiamo in considerazione un gruppo di individui, inclusi quelli che lamentano dolore orofacciale generalmente associato a degenerazione ossea dell'articolazione temporo-mandibolare. Tuttavia, potrebbero esistere altre cause apparentemente non correlate. È necessario tradurre matematicamente la "rilevanza" che queste incertezze causali rivestono nel determinare una diagnosi.
La rilevanza causale
Per affrontare questa questione, consideriamo il grado di rilevanza causale di un evento rispetto a un evento , dove:
- = pazienti con degenerazione ossea dell'articolazione temporo-mandibolare.
- = pazienti che hanno riportato dolore orofacciale.
- = pazienti senza degenerazione ossea dell'articolazione temporo-mandibolare.
La probabilità condizionata è usata per calcolare la probabilità che l'evento si verifichi dato che l'evento si è già verificato.
La rilevanza causale del campione di pazienti si determina come:
dove:
indica la probabilità che alcune persone (tra considerate) soffrano di dolore orofacciale causato dalla degenerazione ossea dell'articolazione temporo-mandibolare,
mentre
indica la probabilità che altre persone (sempre tra considerate) soffrano di dolore orofacciale causato da altri fattori non legati alla degenerazione ossea dell'articolazione temporo-mandibolare.
Poiché tutte le probabilità suggeriscono che , il valore di sarà compreso tra e . I significati attribuibili a questo valore sono:
indica che l'unica causa di dolore orofacciale è la degenerazione ossea dell'ATM,
indica che la degenerazione ossea dell'ATM non è mai la causa del dolore orofacciale, ma sempre qualcos'altro,
indica che la probabilità che il dolore orofacciale sia causato dalla degenerazione ossea dell'ATM o da altri fattori è esattamente la stessa,
e, nei casi intermedi, più realistici:
indica che è più probabile che la degenerazione ossea dell'ATM sia la causa del dolore orofacciale,
indica che è più probabile che la causa del dolore orofacciale non sia la degenerazione ossea dell'ATM.
2° Approccio clinico
Sia quindi la probabilità di identificare, nel nostro campione di persone, individui che presentano gli elementi appartenenti all'insieme specificato . Per utilizzare le informazioni fornite da questo dataset, viene introdotto il concetto di partizione di rilevanza causale:
La partizione della rilevanza causale
Essendo il numero di persone su cui dobbiamo condurre le analisi, se dividiamo questo gruppo, in base a determinate condizioni come spiegato di seguito, in sottoinsiemi con , viene creato un cluster chiamato "set di partizioni" .
dove il simbolismo indica che la sottoclasse è contenuta nel numero .
Per poter definire la partizione come partizione di rilevanza causale, deve possedere queste proprietà:
Per ogni sottoclasse , la condizione deve essere che ovvero la probabilità di trovare nel sottogruppo una persona che presenti i sintomi, i segni clinici e gli elementi appartenenti all'insieme . Una partizione causalmente rilevante di questo tipo viene definita omogenea. Ogni sottoinsieme deve essere 'elementare', cioè non deve essere ulteriormente suddiviso in altri sottoinsiemi, poiché, in tal caso, non avrebbero rilevanza causale.
Assumiamo ora, ad esempio, che il campione di popolazione , a cui appartiene la nostra paziente Mary Poppins, sia una categoria di soggetti dai 20 ai 70 anni. Supponiamo inoltre che in questa popolazione ci siano individui che presentano gli elementi appartenenti al set di dati , corrispondenti alle prove di laboratorio menzionate e descritte in 'La logica del linguaggio classico'.
Supponiamo che in un campione di 10.000 soggetti dai 20 ai 70 anni abbiamo un'incidenza di 30 soggetti che presentano i segni clinici e . Abbiamo scelto di utilizzare questi dati per dimostrare il processo probabilistico perché in letteratura i dati relativi ai segni e sintomi clinici per i disturbi temporo-mandibolari variano ampiamente e presentano un'incidenza che riteniamo eccessivamente alta.
Un esempio di una partizione con presunta probabilità in cui la degenerazione dell'ATM (Deg.TMJ) si verifica in combinazione con i disturbi temporomandibolari (TMD) sarebbe il seguente:
| dove | |||||
| dove | |||||
| dove | |||||
| dove |
Situazioni cliniche
Queste probabilità condizionali dimostrano che ciascuna delle quattro sottoclassi della partizione è causalmente rilevante per i dati del paziente nel campione di popolazione . Date le suddette partizioni della classe di riferimento, abbiamo le seguenti situazioni cliniche:
- Mary Poppins degenerazione dell'articolazione temporo-mandibolare Disturbi temporo-mandibolari
- Mary Poppins degenerazione dell'articolazione temporo-mandibolare no Disturbi temporo-mandibolari
- Mary Poppins no degenerazione dell'articolazione temporo-mandibolare Disturbi temporo-mandibolari
- Mary Poppins no degenerazione dell'articolazione temporo-mandibolare no Disturbi temporo-mandibolari Per arrivare alla diagnosi finale sopra menzionata, abbiamo condotto un'analisi probabilistico-causale dello stato di salute di Mary Poppins, i cui dati iniziali erano .
In generale, possiamo fare riferimento a un processo logico in cui esaminiamo i seguenti elementi:
- Un individuo:
- Il suo set di dati iniziale
- Un campione di popolazione a cui appartiene
- Una probabilità di base
A questo punto, dovremmo introdurre argomentazioni troppo specialistiche che distoglierebbero il lettore dall'argomento principale, ma che hanno un'elevata importanza epistemica. Pertanto, cercheremo di estrarre il filo logico più semplice descritto nel concetto Analysandum/Analysans.
Nell'analisi probabilistico-causale di , si distinguono un paio delle seguenti forme logiche (Analysandum/Analysans):
- Analysandum : è una forma logica che contiene due parametri: la probabilità di selezionare una persona che presenta i sintomi e gli elementi appartenenti all'insieme e il generico individuo incline a quei sintomi.
- Analysan : è una forma logica che contiene tre parametri: la partizione , il generico individuo appartenente al campione di popolazione e la (Conoscenza di base), che comprende un insieme di affermazioni di probabilità condizionata superiori a .
Ad esempio, si può concludere che la diagnosi definitiva sia la seguente:
significa che la nostra Mary Poppins ha il 95% di probabilità di soffrire di Disturbi Temporo-Mandibolari (TMD), in quanto presenta una degenerazione dell'articolazione temporo-mandibolare oltre ad altri indicatori positivi inclusi nel set di dati .
- ↑ Sarkar S, «Nagel on Reduction», in Stud Hist Philos Sci, 2015».
PMID:26386529
DOI:10.1016/j.shpsa.2015.05.006 - ↑ DN model of scientific explanation, also known as Hempel's model, Hempel–Oppenheim model, Popper–Hempel model, or covering law model
- ↑ Pantoja LLQ, De Toledo IP, Pupo YM, Porporatti AL, De Luca Canto G, Zwir LF, Guerra ENS, «Prevalence of degenerative joint disease of the temporomandibular joint: a systematic review», in Clin Oral Investig, 2019».
PMID:30311063
DOI:10.1007/s00784-018-2664-y - ↑ De Toledo IP, Stefani FM, Porporatti AL, Mezzomo LA, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of otologic signs and symptoms in adult patients with temporomandibular disorders: a systematic review and meta-analysis», in Clin Oral Investig, 2017».
PMID:27511214
DOI:10.1007/s00784-016-1926-9 - ↑ Bonotto D, Penteado CA, Namba EL, Cunali PA, Rached RN, Azevedo-Alanis LR, «Prevalence of temporomandibular disorders in rugby players», in Gen Dent».
PMID:31355769 - ↑ da Silva CG, Pachêco-Pereira C, Porporatti AL, Savi MG, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of clinical signs of intra-articular temporomandibular disorders in children and adolescents: A systematic review and meta-analysis», in Am Dent Assoc, 2016». - PMCID:26552334
DOI:10.1016/j.adaj.2015.07.017 - ↑ Gauer RL, Semidey MJ, «Diagnosis and treatment of temporomandibular disorders», in Am Fam Physician, 2015».
PMID:25822556 - ↑ Kohlmann T, «Epidemiology of orofacial pain», in Schmerz, 2002».
PMID:12235497
DOI:10.1007/s004820200000