Difference between revisions of "Store:FLde05"
Gianfranco (talk | contribs) (Created page with "==Fuzzy set <math>\tilde{A}</math> and membership function <math>\mu_{\displaystyle {\tilde {A}}}(x)</math>== We choose - as a formalism - to represent a fuzzy set with the 'tilde':<math>\tilde{A}</math>. A fuzzy set is a set where the elements have a 'degree' of belonging (consistent with fuzzy logic): some can be included in the set at 100%, others in lower percentages. To mathematically represent this degree of belonging is the function <math>\mu_{\displaystyle {\til...") |
|||
| Line 1: | Line 1: | ||
==Fuzzy | ==Fuzzy-Set <math>\tilde{A}</math> und Zugehörigkeitsfunktion <math>\mu_{\displaystyle {\tilde {A}}}(x)</math>== | ||
Wir wählen – als Formalismus – die Darstellung einer Fuzzy-Menge mit der „Tilde“: <math>\tilde{A}</math>. Eine Fuzzy-Menge ist eine Menge, bei der die Elemente einen „Grad“ der Zugehörigkeit haben (in Übereinstimmung mit der Fuzzy-Logik): einige können in die Menge aufgenommen werden bei 100 %, andere in niedrigeren Prozentsätzen. | |||
Um diesen Grad der Zugehörigkeit mathematisch darzustellen, gibt es die Funktion <math>\mu_{\displaystyle {\tilde {A}}}(x)</math>, die „'''Mitgliedschaftsfunktion'''“ genannt wird. Die Funktion <math>\mu_{\displaystyle {\tilde {A}}}(x)</math> ist eine kontinuierliche Funktion, die im Intervall <math>[0;1]</math> definiert ist, wo sie ist: | |||
*<math>\mu_ {\tilde {A}}(x) = 1\rightarrow </math> wenn <math>x</math> vollständig in <math>A</math> enthalten ist (diese Punkte werden "'''Kern'''" genannt, sie zeigen <u>plausible</u> Prädikatswerte an). | |||
*<math>\mu_ {\tilde {A}}(x) = 0\rightarrow </math>wenn <math>x</math> nicht enthalten ist <math>A</math> | |||
*<math>0<\mu_ {\tilde {A}}(x) < 1 \;\rightarrow </math> wenn <math>x</math> teilweise in <math>A</math> enthalten ist (diese Punkte werden 'Unterstützung' genannt, sie geben die möglichen Prädikatswerte an). | |||
*if <math>x</math> is partially contained in <math>A</math> (these points are called ''''support'''<nowiki/>', they indicate the <u>possible</u> predicate values). | |||
Die grafische Darstellung der Funktion <math>\mu_{\displaystyle {\tilde {A}}}(x)</math> kann variiert werden; von solchen mit linearen Linien (dreieckig, trapezförmig) bis hin zu solchen in Form von Glocken oder „S“ (sigmoidal), wie in Abbildung 1 dargestellt, die das gesamte grafische Konzept der Zugehörigkeitsfunktion enthält<ref>{{Cite book | |||
| autore = Zhang W | | autore = Zhang W | ||
| autore2 = Yang J | | autore2 = Yang J | ||
| Line 51: | Line 51: | ||
| OCLC = | | OCLC = | ||
}}</ref> | }}</ref> | ||
[[File:Fuzzy_crisp.svg|alt=|left|thumb|400px|''' | [[File:Fuzzy_crisp.svg|alt=|left|thumb|400px|'''Abbildung 1:''' Arten von Graphen für die Zugehörigkeitsfunktion.]] | ||
Die '''Unterstützungsmenge''' einer Fuzzy-Menge ist definiert als die Zone, in der der Zugehörigkeitsgrad <math>0<\mu_ {\tilde {A}}(x) < 1</math> ergibt; Andererseits wird der Kern als der Bereich definiert, in dem der Grad der Zugehörigkeit den Wert <math>\mu_ {\tilde {A}}(x) = 1</math> annimmt. | |||
Die „Unterstützungsmenge“ stellt die für möglich erachteten Werte des Prädikats dar, während der „'''Kern'''“ die für plausibler erachteten Werte darstellt. | |||
Wenn <math>{A}</math> eine Menge im gewöhnlichen Sinne des oben beschriebenen Begriffs oder der klassischen Sprachlogik darstellen würde, könnte ihre Zugehörigkeitsfunktion nur die Werte <math>1</math> oder <math>0</math> annehmen, <math>\mu_{\displaystyle {{A}}}(x)= 1 \; \lor \;\mu_{\displaystyle {{A}}}(x)= 0</math> je nachdem, ob das Element <math>x</math> zum betrachteten Ganzen gehört oder nicht. Abbildung 2 zeigt eine grafische Darstellung des klaren (starr definierten) oder unscharfen Konzepts der Mitgliedschaft, das deutlich an die Überlegungen von Smuts erinnert.<ref name=":0">•SMUTS J.C. 1926, [[wikipedia:Holism_and_Evolution|<!--139-->Holism and Evolution]], London: Macmillan.</ref> | |||
Gehen wir zurück zum konkreten Fall unserer Mary Poppins, in der wir eine Diskrepanz zwischen den Behauptungen des Zahnarztes und des Neurologen sehen und wir suchen einen Vergleich zwischen klassischer Logik und Fuzzy-Logik: | |||
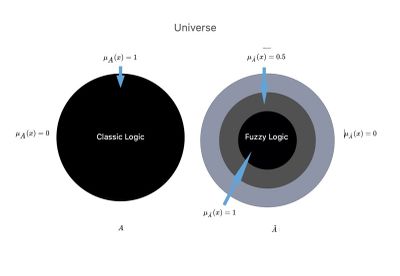
[[File:Fuzzy1.jpg|thumb|400x400px|''' | [[File:Fuzzy1.jpg|thumb|400x400px|'''Abbildung 2:''' Darstellung des Vergleichs zwischen einem klassischen und einem Fuzzy-Ensemble.]] | ||
Abbildung 2: Stellen wir uns das Wissenschaftsuniversum <math>U</math> vor, in dem es zwei parallele Welten oder Kontexte gibt, <math>{A}</math> und <math>\tilde{A}</math> | |||
<math>{A}=</math> | <math>{A}=</math> Im wissenschaftlichen Kontext das sogenannte „Crisp“, und wir haben in die Logik der klassischen Sprache überführt, in der der Arzt eine absolute wissenschaftliche Hintergrundinformation <math>KB</math> mit einer klaren Trennlinie hat, die wir <math>KB_c</math> genannt haben | ||
<math>\tilde{A}=</math> In | <math>\tilde{A}=</math> In einem anderen wissenschaftlichen Kontext, der „Fuzzy-Logik“ genannt wird und in dem es eine Vereinigung zwischen der Teilmenge <math>{A}</math> in <math>\tilde{A}</math> gibt, die wir so weit gehen können zu sagen: Vereinigung zwischen <math>KB_c</math>. | ||
Wir werden die folgenden Abzüge bemerkenswert bemerken: | |||
*''' | *'''Klassische Logik''' im zahnmedizinischen Kontext <math>{A}</math>, in der nur ein logischer Prozess möglich ist, der als Ergebnis <math>\mu_{\displaystyle {{A}}}(x)= 1 </math> liefert, oder <math>\mu_{\displaystyle {{A}}}(x)= 0 </math> ist der Datenbereich <math>D=\{\delta_1,\dots,\delta_4\}</math>, reduziert auf Grundwissen <math>KB</math> in der Menge <math>{A}</math>. Das bedeutet, dass es außerhalb der zahnmedizinischen Welt eine gibt void und dass der Begriff der Mengenlehre genau <math>\mu_{\displaystyle {{A}}}(x)= 0 </math> geschrieben wird und was gleichbedeutend ist mit einem hohen Bereich von: | ||
{{q2| | {{q2|Differentialdiagnosefehler|}} | ||
*'''Fuzzy | *'''Fuzzy-Logik''' im zahnmedizinischen Kontext <math>\tilde{A}</math>, in der sie über das Grundwissen <math>KB</math> hinaus repräsentiert werden des zahnmedizinischen Kontexts haben auch diejenigen, die teilweise aus der neurophysiologischen Welt <math>0<\mu_ {\tilde {A}}(x) < 1</math> erworben wurden, das Vorrecht, ein Ergebnis <math>\mu_\tilde{A}(x)= 1 | ||
</math> | </math> und ein Ergebnis <math>0<\mu_ {\tilde {A}}(x) < 1</math> aufgrund von Grundwissen <math>KB</math> zurückzugeben was an dieser Stelle durch die Vereinigung von <math>KB_c</math> dentalen und neurologischen Kontexten repräsentiert wird. Das Ergebnis dieser wissenschaftlich-klinischen Umsetzung der Zahnheilkunde würde a {{q2|Reduzierung des differenzialdiagnostischen Fehlers|}} | ||
Latest revision as of 19:15, 12 March 2023
Fuzzy-Set und Zugehörigkeitsfunktion
Wir wählen – als Formalismus – die Darstellung einer Fuzzy-Menge mit der „Tilde“: . Eine Fuzzy-Menge ist eine Menge, bei der die Elemente einen „Grad“ der Zugehörigkeit haben (in Übereinstimmung mit der Fuzzy-Logik): einige können in die Menge aufgenommen werden bei 100 %, andere in niedrigeren Prozentsätzen.
Um diesen Grad der Zugehörigkeit mathematisch darzustellen, gibt es die Funktion , die „Mitgliedschaftsfunktion“ genannt wird. Die Funktion ist eine kontinuierliche Funktion, die im Intervall definiert ist, wo sie ist:
- wenn vollständig in enthalten ist (diese Punkte werden "Kern" genannt, sie zeigen plausible Prädikatswerte an).
- wenn nicht enthalten ist
- wenn teilweise in enthalten ist (diese Punkte werden 'Unterstützung' genannt, sie geben die möglichen Prädikatswerte an).
- if is partially contained in (these points are called 'support', they indicate the possible predicate values).
Die grafische Darstellung der Funktion kann variiert werden; von solchen mit linearen Linien (dreieckig, trapezförmig) bis hin zu solchen in Form von Glocken oder „S“ (sigmoidal), wie in Abbildung 1 dargestellt, die das gesamte grafische Konzept der Zugehörigkeitsfunktion enthält[1][2]
Die Unterstützungsmenge einer Fuzzy-Menge ist definiert als die Zone, in der der Zugehörigkeitsgrad ergibt; Andererseits wird der Kern als der Bereich definiert, in dem der Grad der Zugehörigkeit den Wert annimmt.
Die „Unterstützungsmenge“ stellt die für möglich erachteten Werte des Prädikats dar, während der „Kern“ die für plausibler erachteten Werte darstellt.
Wenn eine Menge im gewöhnlichen Sinne des oben beschriebenen Begriffs oder der klassischen Sprachlogik darstellen würde, könnte ihre Zugehörigkeitsfunktion nur die Werte oder annehmen, je nachdem, ob das Element zum betrachteten Ganzen gehört oder nicht. Abbildung 2 zeigt eine grafische Darstellung des klaren (starr definierten) oder unscharfen Konzepts der Mitgliedschaft, das deutlich an die Überlegungen von Smuts erinnert.[3]
Gehen wir zurück zum konkreten Fall unserer Mary Poppins, in der wir eine Diskrepanz zwischen den Behauptungen des Zahnarztes und des Neurologen sehen und wir suchen einen Vergleich zwischen klassischer Logik und Fuzzy-Logik:
Abbildung 2: Stellen wir uns das Wissenschaftsuniversum vor, in dem es zwei parallele Welten oder Kontexte gibt, und
Im wissenschaftlichen Kontext das sogenannte „Crisp“, und wir haben in die Logik der klassischen Sprache überführt, in der der Arzt eine absolute wissenschaftliche Hintergrundinformation mit einer klaren Trennlinie hat, die wir genannt haben
In einem anderen wissenschaftlichen Kontext, der „Fuzzy-Logik“ genannt wird und in dem es eine Vereinigung zwischen der Teilmenge in gibt, die wir so weit gehen können zu sagen: Vereinigung zwischen .
Wir werden die folgenden Abzüge bemerkenswert bemerken:
- Klassische Logik im zahnmedizinischen Kontext , in der nur ein logischer Prozess möglich ist, der als Ergebnis liefert, oder ist der Datenbereich , reduziert auf Grundwissen in der Menge . Das bedeutet, dass es außerhalb der zahnmedizinischen Welt eine gibt void und dass der Begriff der Mengenlehre genau geschrieben wird und was gleichbedeutend ist mit einem hohen Bereich von:
- Fuzzy-Logik im zahnmedizinischen Kontext , in der sie über das Grundwissen hinaus repräsentiert werden des zahnmedizinischen Kontexts haben auch diejenigen, die teilweise aus der neurophysiologischen Welt erworben wurden, das Vorrecht, ein Ergebnis und ein Ergebnis aufgrund von Grundwissen zurückzugeben was an dieser Stelle durch die Vereinigung von dentalen und neurologischen Kontexten repräsentiert wird. Das Ergebnis dieser wissenschaftlich-klinischen Umsetzung der Zahnheilkunde würde a «Reduzierung des differenzialdiagnostischen Fehlers»
- ↑ Zhang W, Yang J, Fang Y, Chen H, Mao Y, Kumar M, «Analytical fuzzy approach to biological data analysis», in Saudi J Biol Sci, 2017».
PMID:28386181 - PMCID:PMC5372457
DOI:10.1016/j.sjbs.2017.01.027 - ↑ Lazar P, Jayapathy R, Torrents-Barrena J, Mol B, Mohanalin, Puig D, «Fuzzy-entropy threshold based on a complex wavelet denoising technique to diagnose Alzheimer disease», in Healthc Technol Lett, The Institution of Engineering and Technology, 2016».
PMID:30800318 - PMCID:PMC6371778
DOI:10.1049/htl.2016.0022 - ↑ •SMUTS J.C. 1926, Holism and Evolution, London: Macmillan.


![{\displaystyle [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3bf59a5da5d8181083b228c8933efbda133483)