Difference between revisions of "Store:LPLes04"
| Line 20: | Line 20: | ||
Consideremos un número <math>n</math> de personas, incluidas las personas que informan dolor orofacial que generalmente tienen degeneración ósea de la articulación temporomandibular. Sin embargo, también pueden existir otras causas aparentemente no relacionadas. Debemos traducir matemáticamente la 'relevancia' que estas incertidumbres causales tienen para determinar un diagnóstico. | Consideremos un número <math>n</math> de personas, incluidas las personas que informan dolor orofacial que generalmente tienen degeneración ósea de la articulación temporomandibular. Sin embargo, también pueden existir otras causas aparentemente no relacionadas. Debemos traducir matemáticamente la 'relevancia' que estas incertidumbres causales tienen para determinar un diagnóstico. | ||
=== | === La relevancia casual === | ||
Para ello consideramos el grado de relevancia causal <math>(cr)</math> de un evento <math>E_1</math> con respecto a un evento <math>E_2</math> donde: | |||
*<math> | *<math>E_1</math> = Pacientes con degeneración ósea de la articulación temporomandibular. | ||
*<math> | *<math>E_2</math> = Pacientes que refieren dolor orofacial. | ||
*<math>E_3</math> = Pacientes sin degeneración ósea de la articulación temporomandibular. | |||
Usaremos la probabilidad condicional <math>P(A \mid B)</math>, que es la probabilidad de que el evento <math>A</math> ocurra solo después de que el evento <math>B</math> ya haya ocurrido. | |||
Con estas premisas la relevancia causal <math>cr</math> de la muestra <math>n</math> de pacientes es: | |||
<math>cr=P(E_2 \mid E_1)- P(E_2 \mid E_3)</math> | |||
dónde | |||
<math> | :<math>P(E_2 \mid E_1)</math> indica la probabilidad de que algunas personas (entre <math>n</math> consideradas) padezcan Dolor Orofacial causado por la degeneración ósea de la Articulación Temporomandibular, | ||
aunque | |||
:<math>P(E_2 \mid | :<math>P(E_2 \mid E_3)</math> indica la probabilidad de que otras personas (siempre entre <math>n</math> considerados) padezcan Dolor Orofacial condicionado por algo distinto a la degeneración ósea de la Articulación Temporomandibular. | ||
: | |||
Dado que todas las probabilidades sugieren que <math>P(A \mid B)</math> es un valor entre <math>0 </math> y <math>1 </math>, el parámetro <math>(cr)</math> será un número que está entre <math>-1 </math> y <math>1 </math> | |||
Los significados que le podemos dar a este número son los siguientes: | |||
*tenemos los casos extremos (que en realidad nunca se dan) que son: | |||
:*<math>cr=1</math> indicando que la única causa del dolor orofacial es la degeneración ósea de la ATM, | |||
* | :*<math>cr=-1</math> lo que indica que la causa del dolor orofacial nunca es la degeneración ósea de la ATM sino otra cosa, | ||
:*<math>cr=0</math> indicando que la probabilidad de que el dolor orofacial sea causado por la degeneración ósea de la ATM o de otra manera es exactamente la misma, | |||
*y los casos intermedios (que son los realistas) | |||
:*<math>cr>0</math> lo que indica que la causa del dolor orofacial es más probable que sea la degeneración ósea de la ATM, | |||
:*<math>cr<0</math> lo que indica que la causa del dolor orofacial probablemente no sea la degeneración ósea de la ATM. | |||
:*<math>cr>0</math> | |||
:*<math>cr<0</math> | |||
<center> | <center> | ||
=== | ===Segundo Enfoque Clínico=== | ||
''( | ''(pasa el cursor sobre las imágenes)'' | ||
<gallery widths="350" heights="282" perrow="2" mode="slideshow"> | <gallery widths="350" heights="282" perrow="2" mode="slideshow"> | ||
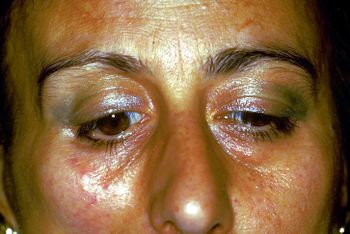
File:Spasmo emimasticatorio.jpg|''' | File:Spasmo emimasticatorio.jpg|'''Figura 1:''' Paciente que refiere "Dolor orofacial en hemilateral derecho" | ||
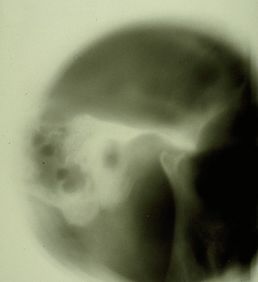
File:Spasmo emimasticatorio ATM.jpg|''' | File:Spasmo emimasticatorio ATM.jpg|'''Figura 2:''' estratigrafía de la ATM del paciente que muestra signos de aplanamiento condilar y osteofito | ||
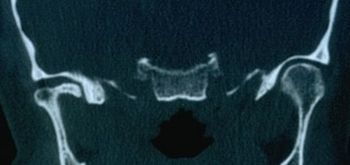
File:Atm1 sclerodermia.jpg|''' | File:Atm1 sclerodermia.jpg|'''Figura 3:''' Tomografía computarizada de la ATM | ||
File:Spasmo emimasticatorio assiografia.jpg|''' | File:Spasmo emimasticatorio assiografia.jpg|'''Figura 4:''' Axiografía del paciente que muestra un aplanamiento del patrón de masticación en el cóndilo derecho | ||
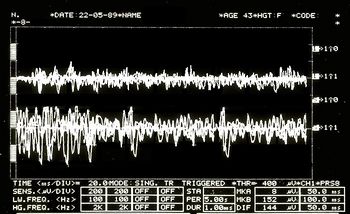
File:EMG2.jpg|''' | File:EMG2.jpg|'''Figura 5:''' Patrón EMG Interferencial. Trazos superiores superpuestos correspondientes al masetero derecho, inferiores al masetero izquierdo. | ||
</gallery> | </gallery> | ||
</center> | </center> | ||
Sea entonces <math>P(D)</math> la probabilidad de encontrar, en la muestra de nuestras <math>n</math> personas, individuos que presenten los elementos pertenecientes al mencionado conjunto <math>D=\{\delta_1,\delta_2,...,\delta_n\}</math> | |||
Para aprovechar la información proporcionada por este conjunto de datos, se introduce el concepto de partición de relevancia causal: | |||
==== | ====La partición de la relevancia causal==== | ||
: | :Siempre sea <math>n</math> el número de personas sobre las que tenemos que realizar los análisis, si dividimos (basado en ciertas condiciones como se explica a continuación) este grupo en <math>k</math> subconjuntos <math>C_i</math> con <math>i=1,2,\dots,k</math>, se crea un grupo que se denomina "conjunto de partición" <math>\pi</math> | ||
:<math>\pi = \{C_1, C_2,\dots,C_k \} \qquad \qquad \text{ | :<math>\pi = \{C_1, C_2,\dots,C_k \} \qquad \qquad \text{con} \qquad \qquad C_i \subset n , </math> | ||
donde con el simbolismo <math>C_i \subset n </math> indica que la subclase <math>C_i</math> está contenida en <math>n</math> | |||
La partición <math>\pi</math>, para que sea definida como una partición de relevancia causal, debe tener estas propiedades: | |||
#Para cada subclase <math>C_i</math> debe aplicarse la condición <math>rc=P(D \mid C_i)- P(D )\neq 0, </math> es decir la probabilidad de encontrar en el subgrupo <math>C_i</math> una persona que presente los síntomas, signos clínicos y elementos pertenecientes al conjunto<math>D=\{\delta_1,\delta_2,...,\delta_n\}</math>. Se dice que una partición causalmente relevante de este tipo es '''homogénea'''. | |||
#Cada subconjunto <math>C_i</math> debe ser 'elemental', es decir, no debe dividirse más en otros subconjuntos, porque si estos existieran no tendrían relevancia causal. | |||
Ahora supongamos, por ejemplo, que la población muestra <math>n</math>, a la que pertenece nuestra buena paciente Mary Poppins, es una categoría de sujetos de 20 a 70 años. Suponemos también que en esta población tenemos a quienes presentan los elementos pertenecientes a la conjunto de datos <math>D=\{\delta_1,.....\delta_n\}</math> que corresponden a las pruebas de laboratorio mencionadas anteriormente y precisamente en '[[The logic of classical language]]'. | |||
</math>. | |||
Supongamos que en una muestra de 10.000 sujetos de 20 a 70 tendremos una incidencia de 30 sujetos <math>p(D)=0.003</math> mostrando signos clínicos <math>\delta_1</math> y <math>\delta_4 | |||
</math>. Preferimos utilizar estos informes para la demostración del proceso probabilístico porque en la literatura los datos referentes a Los signos y síntomas clínicos de los trastornos temporomandibulares tienen una variación demasiado amplia y una incidencia demasiado alta en nuestra opinión.<ref name=":2">{{Cite book | |||
| autore = Pantoja LLQ | | autore = Pantoja LLQ | ||
| autore2 = De Toledo IP | | autore2 = De Toledo IP | ||
| Line 219: | Line 212: | ||
}}</ref> | }}</ref> | ||
Un ejemplo de una partición con presunta probabilidad en la que la degeneración de la ATM (Deg.TMJ) se produce junto con los trastornos temporomandibulares (TMD) sería el siguiente: | |||
{| | {| | ||
|+ | |+ | ||
|<math>P(D| Deg.TMJ \cap TMDs)=0.95 \qquad \qquad \; </math> | |<math>P(D| Deg.TMJ \cap TMDs)=0.95 \qquad \qquad \; </math> | ||
| | | | ||
| | |dónde | ||
| | | | ||
| | | | ||
| Line 231: | Line 224: | ||
|<math>P(D| Deg.TMJ \cap noTMDs)=0.3 \qquad \qquad \quad </math> | |<math>P(D| Deg.TMJ \cap noTMDs)=0.3 \qquad \qquad \quad </math> | ||
| | | | ||
| | |dónde | ||
| | | | ||
| | | | ||
| Line 238: | Line 231: | ||
|<math>P(D| no Deg.TMJ \cap TMDs)=0.199 \qquad \qquad \; </math> | |<math>P(D| no Deg.TMJ \cap TMDs)=0.199 \qquad \qquad \; </math> | ||
| | | | ||
| | |dónde | ||
| | | | ||
| | | | ||
| Line 245: | Line 238: | ||
|<math>P(D| noDeg.TMJ \cap noTMDs)=0.001 \qquad \qquad \;</math> | |<math>P(D| noDeg.TMJ \cap noTMDs)=0.001 \qquad \qquad \;</math> | ||
| | | | ||
| | |dónde | ||
| | | | ||
| | | | ||
| Line 251: | Line 244: | ||
|} | |} | ||
*{{q2|< | *{{q2|Una partición homogénea proporciona lo que estamos acostumbrados a llamar Diagnóstico Diferencial.|}} | ||
====Situaciones clínicas==== | |||
Estas probabilidades condicionales demuestran que cada una de las cuatro subclases de la partición es causalmente relevante para los datos del paciente <math>D=\{\delta_1,.....\delta_n\}</math> en la muestra de población <math>PO</math>. Dada la partición antes mencionada de la clase de referencia, tenemos las siguientes situaciones clínicas: | |||
*Mary Poppins <math>\in</math> Degeneración de la articulación temporomandibular <math>\cap</math> Trastornos temporomandibulares | |||
*Mary Poppins <math>\in</math> | |||
*Mary Poppins <math>\in</math> | *Mary Poppins <math>\in</math> degeneración de la articulación temporomandibular <math>\cap</math> no Trastornos temporomandibulares | ||
*Mary Poppins <math>\in</math> | *Mary Poppins <math>\in</math> sin degeneración de la articulación temporomandibular <math>\cap</math> Trastornos temporomandibulares | ||
*Mary Poppins <math>\in</math> | *Mary Poppins <math>\in</math> sin degeneración de la articulación temporomandibular <math>\cap</math> sin trastornos temporomandibulares | ||
Para llegar al diagnóstico final anterior, realizamos un análisis probabilístico-causal del estado de salud de Mary Poppins cuyos datos iniciales fueron <math>D=\{\delta_1,.....\delta_n\}</math>. | |||
En general, podemos referirnos a un proceso lógico en el que examinamos los siguientes elementos: | |||
* | *un individuo: <math>a</math> | ||
* | *su conjunto de datos inicial<math>D=\{\delta_1,.....\delta_n\}</math> | ||
* | *una muestra de población <math>n</math> a la que pertenece, | ||
* | *una probabilidad básica <math>P(D)=0,003</math> | ||
En este punto conviene introducir argumentos demasiado especializados que alejarían al lector del tema pero que tienen una gran importancia epistémica por lo que intentaremos extraer el hilo lógico más descrito del concepto Analysandum/Analysans. | |||
El análisis probabilístico-causal de <math>D=\{\delta_1,.....\delta_n\}</math> es entonces un par de las siguientes formas lógicas (Analysandum / Analysans<ref>{{Cite book | |||
| autore = Westmeyer H | | autore = Westmeyer H | ||
| titolo = The diagnostic process as a statistical-causal analysis | | titolo = The diagnostic process as a statistical-causal analysis | ||
| Line 290: | Line 284: | ||
| OCLC = | | OCLC = | ||
}}</ref>): | }}</ref>): | ||
*'''Analysandum''' <math> = \{P(D),a\}</math>: | *'''Analysandum''' <math> = \{P(D),a\}</math>: es una forma lógica que contiene dos parámetros: probabilidad <math>P(D)</math> de seleccionar una persona que tenga los síntomas y elementos pertenecientes al conjunto <math>D=\{\delta_1,\delta_2,...,\delta_n\}</math>, y el individuo genérico <math>a</math> que es propenso a esos síntomas. | ||
*'''Analysan <math>= \{\pi,a,KB\}</math>''': | *'''Analysan''' '''<math>= \{\pi,a,KB\}</math>''': es una forma lógica que contiene tres parámetros: la partición <math>\pi</math>, el individuo genérico <math>a</math> perteneciente a la muestra poblacional <math>n</math> y ''<math>KB</math>'' (Base de Conocimiento) que incluye un conjunto de <math>n>1</math> enunciados de probabilidad condicionada. | ||
Por ejemplo, se puede concluir que el diagnóstico definitivo es el siguiente: | |||
<math>P(D| Deg.TMJ \cap TMDs)=0.95</math> - | <math>P(D| Deg.TMJ \cap TMDs)=0.95</math> - esto significa que nuestra Mary Poppins está afectada en un 95% por TTM, ya que tiene una degeneración de la Articulación Temporomandibular además de los datos positivos <math>D=\{\delta_1,.....\delta_n\}</math> | ||
Latest revision as of 11:16, 11 March 2023
Análisis probabilístico-causal
De estas premisas se desprende que el diagnóstico clínico se realiza mediante el denominado método hipotético-deductivo denominado DN[1] (modelo deductivo-nomológico)[2]. Pero esto no es realista, ya que el conocimiento médico utilizado en la toma de decisiones clínicas difícilmente contiene leyes deterministas causales que permitan explicaciones causales y, por tanto, formular diagnósticos clínicos, entre otras cosas en el contexto del especialista. Intentemos analizar nuevamente el caso de nuestra Mary Poppins, esta vez intentando un enfoque probabilístico-causal.
Consideremos un número de personas, incluidas las personas que informan dolor orofacial que generalmente tienen degeneración ósea de la articulación temporomandibular. Sin embargo, también pueden existir otras causas aparentemente no relacionadas. Debemos traducir matemáticamente la 'relevancia' que estas incertidumbres causales tienen para determinar un diagnóstico.
La relevancia casual
Para ello consideramos el grado de relevancia causal de un evento con respecto a un evento donde:
- = Pacientes con degeneración ósea de la articulación temporomandibular.
- = Pacientes que refieren dolor orofacial.
- = Pacientes sin degeneración ósea de la articulación temporomandibular.
Usaremos la probabilidad condicional , que es la probabilidad de que el evento ocurra solo después de que el evento ya haya ocurrido.
Con estas premisas la relevancia causal de la muestra de pacientes es:
dónde
- indica la probabilidad de que algunas personas (entre consideradas) padezcan Dolor Orofacial causado por la degeneración ósea de la Articulación Temporomandibular,
aunque
- indica la probabilidad de que otras personas (siempre entre considerados) padezcan Dolor Orofacial condicionado por algo distinto a la degeneración ósea de la Articulación Temporomandibular.
Dado que todas las probabilidades sugieren que es un valor entre y , el parámetro será un número que está entre y
Los significados que le podemos dar a este número son los siguientes:
- tenemos los casos extremos (que en realidad nunca se dan) que son:
- indicando que la única causa del dolor orofacial es la degeneración ósea de la ATM,
- lo que indica que la causa del dolor orofacial nunca es la degeneración ósea de la ATM sino otra cosa,
- indicando que la probabilidad de que el dolor orofacial sea causado por la degeneración ósea de la ATM o de otra manera es exactamente la misma,
- y los casos intermedios (que son los realistas)
- lo que indica que la causa del dolor orofacial es más probable que sea la degeneración ósea de la ATM,
- lo que indica que la causa del dolor orofacial probablemente no sea la degeneración ósea de la ATM.
Segundo Enfoque Clínico
(pasa el cursor sobre las imágenes)
Sea entonces la probabilidad de encontrar, en la muestra de nuestras personas, individuos que presenten los elementos pertenecientes al mencionado conjunto
Para aprovechar la información proporcionada por este conjunto de datos, se introduce el concepto de partición de relevancia causal:
La partición de la relevancia causal
- Siempre sea el número de personas sobre las que tenemos que realizar los análisis, si dividimos (basado en ciertas condiciones como se explica a continuación) este grupo en subconjuntos con , se crea un grupo que se denomina "conjunto de partición"
donde con el simbolismo indica que la subclase está contenida en
La partición , para que sea definida como una partición de relevancia causal, debe tener estas propiedades:
- Para cada subclase debe aplicarse la condición es decir la probabilidad de encontrar en el subgrupo una persona que presente los síntomas, signos clínicos y elementos pertenecientes al conjunto. Se dice que una partición causalmente relevante de este tipo es homogénea.
- Cada subconjunto debe ser 'elemental', es decir, no debe dividirse más en otros subconjuntos, porque si estos existieran no tendrían relevancia causal.
Ahora supongamos, por ejemplo, que la población muestra , a la que pertenece nuestra buena paciente Mary Poppins, es una categoría de sujetos de 20 a 70 años. Suponemos también que en esta población tenemos a quienes presentan los elementos pertenecientes a la conjunto de datos que corresponden a las pruebas de laboratorio mencionadas anteriormente y precisamente en 'The logic of classical language'.
Supongamos que en una muestra de 10.000 sujetos de 20 a 70 tendremos una incidencia de 30 sujetos mostrando signos clínicos y . Preferimos utilizar estos informes para la demostración del proceso probabilístico porque en la literatura los datos referentes a Los signos y síntomas clínicos de los trastornos temporomandibulares tienen una variación demasiado amplia y una incidencia demasiado alta en nuestra opinión.[3][4][5][6][7][8]
Un ejemplo de una partición con presunta probabilidad en la que la degeneración de la ATM (Deg.TMJ) se produce junto con los trastornos temporomandibulares (TMD) sería el siguiente:
| dónde | |||||
| dónde | |||||
| dónde | |||||
| dónde |
- «Una partición homogénea proporciona lo que estamos acostumbrados a llamar Diagnóstico Diferencial.»
Situaciones clínicas
Estas probabilidades condicionales demuestran que cada una de las cuatro subclases de la partición es causalmente relevante para los datos del paciente en la muestra de población . Dada la partición antes mencionada de la clase de referencia, tenemos las siguientes situaciones clínicas:
- Mary Poppins Degeneración de la articulación temporomandibular Trastornos temporomandibulares
- Mary Poppins degeneración de la articulación temporomandibular no Trastornos temporomandibulares
- Mary Poppins sin degeneración de la articulación temporomandibular Trastornos temporomandibulares
- Mary Poppins sin degeneración de la articulación temporomandibular sin trastornos temporomandibulares
Para llegar al diagnóstico final anterior, realizamos un análisis probabilístico-causal del estado de salud de Mary Poppins cuyos datos iniciales fueron .
En general, podemos referirnos a un proceso lógico en el que examinamos los siguientes elementos:
- un individuo:
- su conjunto de datos inicial
- una muestra de población a la que pertenece,
- una probabilidad básica
En este punto conviene introducir argumentos demasiado especializados que alejarían al lector del tema pero que tienen una gran importancia epistémica por lo que intentaremos extraer el hilo lógico más descrito del concepto Analysandum/Analysans.
El análisis probabilístico-causal de es entonces un par de las siguientes formas lógicas (Analysandum / Analysans[9]):
- Analysandum : es una forma lógica que contiene dos parámetros: probabilidad de seleccionar una persona que tenga los síntomas y elementos pertenecientes al conjunto , y el individuo genérico que es propenso a esos síntomas.
- Analysan : es una forma lógica que contiene tres parámetros: la partición , el individuo genérico perteneciente a la muestra poblacional y (Base de Conocimiento) que incluye un conjunto de enunciados de probabilidad condicionada.
Por ejemplo, se puede concluir que el diagnóstico definitivo es el siguiente:
- esto significa que nuestra Mary Poppins está afectada en un 95% por TTM, ya que tiene una degeneración de la Articulación Temporomandibular además de los datos positivos
- ↑ Sarkar S, «Nagel on Reduction», in Stud Hist Philos Sci, 2015».
PMID:26386529
DOI:10.1016/j.shpsa.2015.05.006 - ↑ DN model of scientific explanation, also known as Hempel's model, Hempel–Oppenheim model, Popper–Hempel model, or covering law model
- ↑ Pantoja LLQ, De Toledo IP, Pupo YM, Porporatti AL, De Luca Canto G, Zwir LF, Guerra ENS, «Prevalence of degenerative joint disease of the temporomandibular joint: a systematic review», in Clin Oral Investig, 2019».
PMID:30311063
DOI:10.1007/s00784-018-2664-y - ↑ De Toledo IP, Stefani FM, Porporatti AL, Mezzomo LA, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of otologic signs and symptoms in adult patients with temporomandibular disorders: a systematic review and meta-analysis», in Clin Oral Investig, 2017».
PMID:27511214
DOI:10.1007/s00784-016-1926-9 - ↑ Bonotto D, Penteado CA, Namba EL, Cunali PA, Rached RN, Azevedo-Alanis LR, «Prevalence of temporomandibular disorders in rugby players», in Gen Dent».
PMID:31355769 - ↑ da Silva CG, Pachêco-Pereira C, Porporatti AL, Savi MG, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of clinical signs of intra-articular temporomandibular disorders in children and adolescents: A systematic review and meta-analysis», in Am Dent Assoc, 2016». - PMCID:26552334
DOI:10.1016/j.adaj.2015.07.017 - ↑ Gauer RL, Semidey MJ, «Diagnosis and treatment of temporomandibular disorders», in Am Fam Physician, 2015».
PMID:25822556 - ↑ Kohlmann T, «Epidemiology of orofacial pain», in Schmerz, 2002».
PMID:12235497
DOI:10.1007/s004820200000 - ↑ Westmeyer H, «The diagnostic process as a statistical-causal analysis», in APA, 1975».
DOI:10.1007/BF00139821
This is an Open Access resource!