Difference between revisions of "Store:LPLde04"
Gianfranco (talk | contribs) (Created page with "==Probabilistic-causal analysis== From these premises it is clear that the clinical diagnosis is made using the so-called hypothetical-deductive method referred to as DN<ref name=":1">{{Cite book | autore = Sarkar S | titolo = Nagel on Reduction | url = https://pubmed.ncbi.nlm.nih.gov/26386529/ | volume = | opera = Stud Hist Philos Sci | anno = 2015 | editore = | città = | ISBN = | PMID = 26386529 | PMCID = | DOI = 10.1016/j.shpsa.2015.05.006 | oaf...") |
|||
| Line 1: | Line 1: | ||
== | ==Probabilistisch-kausale Analyse== | ||
Aus diesen Prämissen geht hervor, dass die klinische Diagnose nach der sogenannten hypothetisch-deduktiven Methode, DN genannt, gestellt wird<ref name=":1">{{Cite book | |||
| autore = Sarkar S | | autore = Sarkar S | ||
| titolo = Nagel on Reduction | | titolo = Nagel on Reduction | ||
| Line 16: | Line 16: | ||
| LCCN = | | LCCN = | ||
| OCLC = | | OCLC = | ||
}}</ref> ([[wikipedia:Deductive-nomological_model|deductive-nomological model]]<ref>''<!--52-->DN model of scientific explanation'', <!--53-->also known as ''<!--54-->Hempel's model'', ''Hempel–Oppenheim model'', ''Popper–Hempel model'', <!--55-->or ''<!--56-->covering law model''</ref>). | }}</ref> ([[wikipedia:Deductive-nomological_model|deductive-nomological model]]<ref>''<!--52-->DN model of scientific explanation'', <!--53-->also known as ''<!--54-->Hempel's model'', ''Hempel–Oppenheim model'', ''Popper–Hempel model'', <!--55-->or ''<!--56-->covering law model''</ref>).Dies ist jedoch unrealistisch, da das in der klinischen Entscheidungsfindung verwendete medizinische Wissen kaum kausaldeterministische Gesetzmäßigkeiten enthält, um kausale Erklärungen zu ermöglichen und damit ua im Fachkontext klinische Diagnosen zu formulieren. Lassen Sie uns versuchen, den Fall unserer Mary Poppins erneut zu analysieren, diesmal versuchen wir es mit einem probabilistisch-kausalen Ansatz. | ||
Betrachten wir eine Anzahl <math>n</math> von Personen, einschließlich Personen, die über orofaziale Schmerzen berichten und im Allgemeinen eine Knochendegeneration des Kiefergelenks haben. Es kann jedoch auch andere scheinbar unabhängige Ursachen geben. Wir müssen die „Relevanz“, die diese kausalen Ungewissheiten für die Bestimmung einer Diagnose haben, mathematisch übersetzen. | |||
=== | ===Die beiläufige Relevanz=== | ||
Dazu betrachten wir den Grad der kausalen Relevanz <math>(cr)</math> eines Ereignisses <math>E_1</math> in Bezug auf ein Ereignis <math>E_2</math>, wobei gilt: | |||
*<math> | *<math>E_1</math> = Patienten mit Knochendegeneration des Kiefergelenks | ||
*<math> | *<math>E_2</math> = Patienten, die über orofaziale Schmerzen berichten | ||
*<math>E_3</math> =Patienten ohne Knochendegeneration des Kiefergelenks. | |||
Wir verwenden die bedingte Wahrscheinlichkeit <math>P(A \mid B)</math>, also die Wahrscheinlichkeit, dass das Ereignis <math>A</math> erst eintritt, nachdem das Ereignis <math>B</math> bereits eingetreten ist. | |||
Mit diesen Prämissen ist die kausale Relevanz <math>cr</math> der Patientenstichprobe <math>n</math>: | |||
<math>cr=P(E_2 \mid E_1)- P(E_2 \mid E_3)</math> | <math>cr=P(E_2 \mid E_1)- P(E_2 \mid E_3)</math> | ||
Wo | |||
:<math>P(E_2 \mid E_1)</math> gibt die Wahrscheinlichkeit an, dass einige Personen (von <math>n</math> berücksichtigten Personen) an orofazialen Schmerzen leiden, die durch eine Knochendegeneration des Kiefergelenks verursacht werden, | |||
:<math>P(E_2 \mid E_3)</math> | während | ||
:<math>P(E_2 \mid E_3)</math> gibt die Wahrscheinlichkeit an, dass andere Personen (immer unter <math>n</math> berücksichtigt) an orofazialen Schmerzen leiden, die durch etwas anderes als eine Knochendegeneration des Kiefergelenks bedingt sind. | |||
: | |||
Da aller Wahrscheinlichkeit nach <math>P(A \mid B)</math> ein Wert zwischen <math>0 </math> und <math>1 </math> ist, wird der Parameter <math>(cr)</math> eine Zahl zwischen <math>-1 </math> und <math>1 </math> sein | |||
Die Bedeutungen, die wir dieser Zahl geben können, sind wie folgt. | |||
*wir haben die extremen Fälle (die in Wirklichkeit nie vorkommen), die sind: | |||
:*<math>cr=1</math> was darauf hinweist, dass die einzige Ursache für orofaziale Schmerzen die Knochendegeneration des Kiefergelenks ist, | |||
* | :*<math>cr=-1</math> was darauf hindeutet, dass die Ursache für orofaziale Schmerzen niemals eine Knochendegeneration des Kiefergelenks ist, sondern etwas anderes, | ||
:*<math>cr=0</math> was darauf hinweist, dass die Wahrscheinlichkeit, dass orofaziale Schmerzen durch Knochendegeneration des Kiefergelenks oder auf andere Weise verursacht werden, genau gleich ist, | |||
*und die Zwischenfälle (die die realistischen sind) | |||
* | :*<math>cr>0</math> was darauf hindeutet, dass die Ursache für orofaziale Schmerzen eher eine Knochendegeneration des Kiefergelenks ist, | ||
:*<math>cr<0</math> was darauf hindeutet, dass die Ursache für orofaziale Schmerzen eher nicht die Knochendegeneration des Kiefergelenks ist. | |||
<center> | |||
'''Zweiter klinischer Ansatz''' | |||
''(fahren Sie mit der Maus über die Bilder)'' | |||
''( | |||
<gallery widths="350" heights="282" perrow="2" mode="slideshow"> | <gallery widths="350" heights="282" perrow="2" mode="slideshow"> | ||
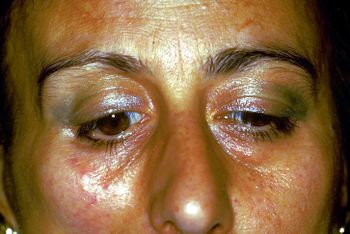
File:Spasmo emimasticatorio.jpg|''' | File:Spasmo emimasticatorio.jpg|'''Abbildung 1:''' Patientenbericht „Orofaziale Schmerzen rechts hemilateral“ | ||
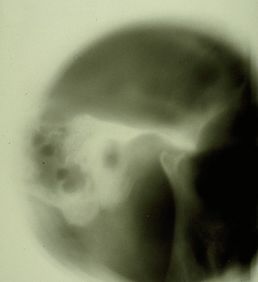
File:Spasmo emimasticatorio ATM.jpg|''' | File:Spasmo emimasticatorio ATM.jpg|'''Abbildung 2:''' Kiefergelenk-Stratigraphie des Patienten mit Anzeichen von Kondylenabflachung und Osteophyten | ||
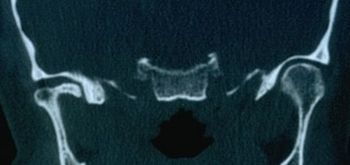
File:Atm1 sclerodermia.jpg|''' | File:Atm1 sclerodermia.jpg|'''Abbildung 3:''' Computertomographie des Kiefergelenks | ||
File:Spasmo emimasticatorio assiografia.jpg|''' | File:Spasmo emimasticatorio assiografia.jpg|'''Abbildung 4:''' Axiographie des Patienten, die eine Abflachung des Kaumusters am rechten Kondylus zeigt | ||
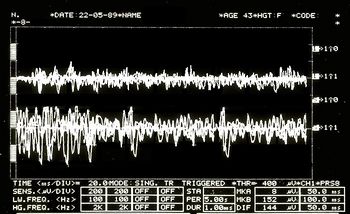
File:EMG2.jpg|''' | File:EMG2.jpg|'''Abbildung 5:''' EMG-Interferenzmuster. Überlappende obere Spuren entsprechen dem rechten Masseter, untere dem linken Masseter. | ||
</gallery> | </gallery> | ||
</center> | </center> | ||
Also sei es dann <math>P(D)</math> die Wahrscheinlichkeit, in der Stichprobe unserer <math>n</math> Personen Personen zu finden, die die Elemente aufweisen, die zu der oben genannten Menge <math>D=\{\delta_1,\delta_2,...,\delta_n\}</math> gehören. | |||
: | Um die Informationen aus diesem Datensatz zu nutzen, wird das Konzept der Aufteilung der kausalen Relevanz eingeführt: | ||
====Die Aufteilung der kausalen Relevanz==== | |||
:<math>\pi = \{C_1, C_2,\dots,C_k \} \qquad \qquad \text{ | :Sei immer <math>n</math> die Anzahl der Personen, für die wir die Analysen durchführen müssen, wenn wir (basierend auf bestimmten Bedingungen, wie unten erklärt) diese Gruppe in <math>k</math> Teilmengen <math>C_i</math> mit <math>i=1,2,\dots,k</math> aufteilen, wird ein Cluster erstellt, der als "Partitionsmenge" <math>\pi</math> bezeichnet wird: | ||
:<math>\pi = \{C_1, C_2,\dots,C_k \} \qquad \qquad \text{mit} \qquad \qquad C_i \subset n , </math> | |||
wobei mit der Symbolik <math>C_i \subset n </math> anzeigt, dass die Unterklasse <math>C_i</math> in <math>n</math> enthalten ist. Die Partition <math>\pi</math> muss, um als Partition mit kausaler Relevanz definiert zu werden, diese Eigenschaften haben: | |||
#Für jede Unterklasse <math>C_i</math> muss die Bedingung <math>rc=P(D \mid C_i)- P(D )\neq 0, </math> gelten, dh die Wahrscheinlichkeit, in der Untergruppe <math>C_i</math> eine Person zu finden, die die zur Menge <math>D=\{\delta_1,\delta_2,...,\delta_n\}</math> gehörenden Symptome, Krankheitszeichen und Elemente aufweist. Eine solche kausal relevante Partition wird als '''homogen bezeichnet'''. | |||
#Jede Teilmenge <math>C_i</math> muss „elementar“ sein, d. h. sie darf nicht weiter in andere Teilmengen unterteilt werden, denn wenn diese existierten, hätten sie keine kausale Bedeutung. | |||
Nehmen wir nun beispielsweise an, dass die Populationsstichprobe <math>n</math>, zu der unsere gute Patientin Mary Poppins gehört, eine Kategorie von Probanden im Alter von 20 bis 70 Jahren ist. Wir nehmen auch an, dass wir in dieser Population diejenigen haben, die die Elemente präsentieren, die zu der gehören Datensatz <math>D=\{\delta_1,.....\delta_n\}</math> die den oben genannten Labortests entsprechen und precisa in '[[The logic of classical language]]'. | |||
Nehmen wir an, dass wir in einer Stichprobe von 10.000 Probanden von 20 bis 70 eine Inzidenz von 30 Probanden <math>p(D)=0.003</math> haben, die klinische Anzeichen von <math>\delta_1</math> und <math>\delta_4 | |||
</math>. | </math> zeigen. Wir haben es vorgezogen, diese Berichte zur Demonstration des probabilistischen Prozesses zu verwenden, da in der Literatur die Daten bzgl Klinische Anzeichen und Symptome für Kiefergelenkserkrankungen weisen unserer Meinung nach eine zu große Variation sowie eine zu hohe Inzidenz auf.<ref name=":2">{{Cite book | ||
| autore = Pantoja LLQ | | autore = Pantoja LLQ | ||
| autore2 = De Toledo IP | | autore2 = De Toledo IP | ||
| Line 208: | Line 208: | ||
}}</ref> | }}</ref> | ||
Ein Beispiel für eine Partition mit vermuteter Wahrscheinlichkeit, bei der eine Kiefergelenksdegeneration (Grad.TMJ) in Verbindung mit Kiefergelenkserkrankungen (TMDs) auftritt, wäre die folgende: | |||
{| | {| | ||
|+ | |+ | ||
|<math>P(D| Deg.TMJ \cap TMDs)=0.95 \qquad \qquad \; </math> | |<math>P(D| Deg.TMJ \cap TMDs)=0.95 \qquad \qquad \; </math> | ||
| | |Wo | ||
| | | | ||
|<math>\C_1 \equiv Deg.TMJ \cap TMDs</math> | |<math>\C_1 \equiv Deg.TMJ \cap TMDs</math> | ||
|- | |- | ||
|<math>P(D| Deg.TMJ \cap noTMDs)=0.3 \qquad \qquad \quad </math> | |<math>P(D| Deg.TMJ \cap noTMDs)=0.3 \qquad \qquad \quad </math> | ||
| | |Wo | ||
| | | | ||
|<math>C_2\equiv Deg.TMJ \cap noTMDs</math> | |<math>C_2\equiv Deg.TMJ \cap noTMDs</math> | ||
|- | |- | ||
|<math>P(D| no Deg.TMJ \cap TMDs)=0.199 \qquad \qquad \; </math> | |<math>P(D| no Deg.TMJ \cap TMDs)=0.199 \qquad \qquad \; </math> | ||
| | |Wo | ||
| | | | ||
|<math>C_3\equiv no Deg.TMJ \cap TMDs</math> | |<math>C_3\equiv no Deg.TMJ \cap TMDs</math> | ||
|- | |- | ||
|<math>P(D| noDeg.TMJ \cap noTMDs)=0.001 \qquad \qquad \;</math> | |<math>P(D| noDeg.TMJ \cap noTMDs)=0.001 \qquad \qquad \;</math> | ||
| | |Wo | ||
| | | | ||
|<math> C_4\equiv noDeg.TMJ \cap noTMDs</math> | |<math> C_4\equiv noDeg.TMJ \cap noTMDs</math> | ||
| Line 242: | Line 235: | ||
*{{q2|<!--107-->A homogeneous partition provides what we are used to calling Differential Diagnosis.|}} | *{{q2|<!--107-->A homogeneous partition provides what we are used to calling Differential Diagnosis.|}} | ||
==== | ====Klinische Situationen==== | ||
Diese bedingten Wahrscheinlichkeiten demonstrieren, dass jede der vier Unterklassen der Partition kausal relevant für die Patientendaten <math>D=\{\delta_1,.....\delta_n\}</math> in der Bevölkerungsstichprobe<math>PO</math> ist. Angesichts der oben erwähnten Partition der Referenzklasse haben wir die folgenden klinischen Situationen: | |||
*Mary Poppins <math>\in</math> | *Mary Poppins <math>\in</math> Degeneration des Kiefergelenks <math>\cap</math> Kiefergelenkserkrankungen | ||
*Mary Poppins <math>\in</math> | *Mary Poppins <math>\in</math> Degeneration des Kiefergelenks <math>\cap</math> keine Kiefergelenkserkrankungen | ||
*Mary Poppins <math>\in</math> | *Mary Poppins <math>\in</math> keine Degeneration des Kiefergelenks <math>\cap</math> Kiefergelenkserkrankungen | ||
*Mary Poppins <math>\in</math> keine Degeneration des Kiefergelenks <math>\cap</math> keine Kiefergelenkserkrankungen | |||
Um zu der obigen endgültigen Diagnose zu gelangen, führten wir eine probabilistisch-kausale Analyse des Gesundheitszustands von Mary Poppins durch, deren Ausgangsdaten <math>D=\{\delta_1,.....\delta_n\}</math> waren. | |||
Im Allgemeinen können wir von einem logischen Prozess sprechen, in dem wir die folgenden Elemente untersuchen: | |||
*ein Individuum: <math>a</math> | |||
*seinen Anfangsdatensatz <math>D=\{\delta_1,.....\delta_n\}</math> | |||
*eine Populationsstichprobe <math>n</math>, zu der es gehört, | |||
*eine Basiswahrscheinlichkeit <math>P(D)=0,003</math> | |||
An dieser Stelle sollten wir zu spezialisierte Argumente einführen, die den Leser vom Thema ablenken würden, die aber eine hohe epistemische Bedeutung haben, für die wir versuchen werden, den am besten beschriebenen logischen Faden des Analysandum/Analysans-Konzepts herauszuziehen. Die probabilistisch-kausale Analyse von <math>D=\{\delta_1,.....\delta_n\}</math> ist dann ein Paar der folgenden logischen Formen (Analysandum / Analysans<ref>{{Cite book | |||
| autore = Westmeyer H | | autore = Westmeyer H | ||
| titolo = The diagnostic process as a statistical-causal analysis | | titolo = The diagnostic process as a statistical-causal analysis | ||
| Line 279: | Line 271: | ||
| OCLC = | | OCLC = | ||
}}</ref>): | }}</ref>): | ||
*''' | *'''Analysand''' <math> = \{P(D),a\}</math>: ist eine logische Form, die zwei Parameter enthält: Wahrscheinlichkeit <math>P(D)</math>, eine Person auszuwählen, die die Symptome und Elemente hat, die zur Menge <math>D=\{\delta_1,\delta_2,...,\delta_n\}</math> gehören, und die generische Person <math>a</math>, die für diese Symptome anfällig ist. | ||
*'''Analysator <math>= \{\pi,a,KB\}</math>''': ist eine logische Form, die drei Parameter enthält: die Partition <math>\pi</math>, die generische Person <math>a</math>, die zur Populationsstichprobe <math>n</math> gehört, und ''<math>KB</math>'' (Wissensbasis), die einen Satz von <math>n>1</math> Aussagen zur bedingten Wahrscheinlichkeit enthält. | |||
Beispielsweise kann daraus geschlossen werden, dass die definitive Diagnose die folgende ist: | |||
<math>P(D| Deg.TMJ \cap TMDs)=0.95</math> bedeutet das, dass unsere Mary Poppins zu 95% von CMDs betroffen ist, da sie zusätzlich zu den positiven Daten eine Degeneration des Kiefergelenks hat <math>D=\{\delta_1,.....\delta_n\}</math> | |||
For example, it can be concluded that the definitive diagnosis is the following: | For example, it can be concluded that the definitive diagnosis is the following: | ||
<math>P(D| Deg.TMJ \cap TMDs)=0.95</math> - this means that our Mary Poppins is 95% affected by TMDs, since she has a degeneration of the Temporomandibular Joint in addition to the positive data <math>D=\{\delta_1,.....\delta_n\}</math> | <math>P(D| Deg.TMJ \cap TMDs)=0.95</math> - this means that our Mary Poppins is 95% affected by TMDs, since she has a degeneration of the Temporomandibular Joint in addition to the positive data <math>D=\{\delta_1,.....\delta_n\}</math> | ||
Revision as of 10:32, 10 March 2023
Probabilistisch-kausale Analyse
Aus diesen Prämissen geht hervor, dass die klinische Diagnose nach der sogenannten hypothetisch-deduktiven Methode, DN genannt, gestellt wird[1] (deductive-nomological model[2]).Dies ist jedoch unrealistisch, da das in der klinischen Entscheidungsfindung verwendete medizinische Wissen kaum kausaldeterministische Gesetzmäßigkeiten enthält, um kausale Erklärungen zu ermöglichen und damit ua im Fachkontext klinische Diagnosen zu formulieren. Lassen Sie uns versuchen, den Fall unserer Mary Poppins erneut zu analysieren, diesmal versuchen wir es mit einem probabilistisch-kausalen Ansatz.
Betrachten wir eine Anzahl von Personen, einschließlich Personen, die über orofaziale Schmerzen berichten und im Allgemeinen eine Knochendegeneration des Kiefergelenks haben. Es kann jedoch auch andere scheinbar unabhängige Ursachen geben. Wir müssen die „Relevanz“, die diese kausalen Ungewissheiten für die Bestimmung einer Diagnose haben, mathematisch übersetzen.
Die beiläufige Relevanz
Dazu betrachten wir den Grad der kausalen Relevanz eines Ereignisses in Bezug auf ein Ereignis , wobei gilt:
- = Patienten mit Knochendegeneration des Kiefergelenks
- = Patienten, die über orofaziale Schmerzen berichten
- =Patienten ohne Knochendegeneration des Kiefergelenks.
Wir verwenden die bedingte Wahrscheinlichkeit , also die Wahrscheinlichkeit, dass das Ereignis erst eintritt, nachdem das Ereignis bereits eingetreten ist.
Mit diesen Prämissen ist die kausale Relevanz der Patientenstichprobe :
Wo
- gibt die Wahrscheinlichkeit an, dass einige Personen (von berücksichtigten Personen) an orofazialen Schmerzen leiden, die durch eine Knochendegeneration des Kiefergelenks verursacht werden,
während
- gibt die Wahrscheinlichkeit an, dass andere Personen (immer unter berücksichtigt) an orofazialen Schmerzen leiden, die durch etwas anderes als eine Knochendegeneration des Kiefergelenks bedingt sind.
Da aller Wahrscheinlichkeit nach ein Wert zwischen und ist, wird der Parameter eine Zahl zwischen und sein
Die Bedeutungen, die wir dieser Zahl geben können, sind wie folgt.
- wir haben die extremen Fälle (die in Wirklichkeit nie vorkommen), die sind:
- was darauf hinweist, dass die einzige Ursache für orofaziale Schmerzen die Knochendegeneration des Kiefergelenks ist,
- was darauf hindeutet, dass die Ursache für orofaziale Schmerzen niemals eine Knochendegeneration des Kiefergelenks ist, sondern etwas anderes,
- was darauf hinweist, dass die Wahrscheinlichkeit, dass orofaziale Schmerzen durch Knochendegeneration des Kiefergelenks oder auf andere Weise verursacht werden, genau gleich ist,
- und die Zwischenfälle (die die realistischen sind)
- was darauf hindeutet, dass die Ursache für orofaziale Schmerzen eher eine Knochendegeneration des Kiefergelenks ist,
- was darauf hindeutet, dass die Ursache für orofaziale Schmerzen eher nicht die Knochendegeneration des Kiefergelenks ist.
Zweiter klinischer Ansatz
(fahren Sie mit der Maus über die Bilder)
Also sei es dann die Wahrscheinlichkeit, in der Stichprobe unserer Personen Personen zu finden, die die Elemente aufweisen, die zu der oben genannten Menge gehören.
Um die Informationen aus diesem Datensatz zu nutzen, wird das Konzept der Aufteilung der kausalen Relevanz eingeführt:
Die Aufteilung der kausalen Relevanz
- Sei immer die Anzahl der Personen, für die wir die Analysen durchführen müssen, wenn wir (basierend auf bestimmten Bedingungen, wie unten erklärt) diese Gruppe in Teilmengen mit aufteilen, wird ein Cluster erstellt, der als "Partitionsmenge" bezeichnet wird:
wobei mit der Symbolik anzeigt, dass die Unterklasse in enthalten ist. Die Partition muss, um als Partition mit kausaler Relevanz definiert zu werden, diese Eigenschaften haben:
- Für jede Unterklasse muss die Bedingung gelten, dh die Wahrscheinlichkeit, in der Untergruppe eine Person zu finden, die die zur Menge gehörenden Symptome, Krankheitszeichen und Elemente aufweist. Eine solche kausal relevante Partition wird als homogen bezeichnet.
- Jede Teilmenge muss „elementar“ sein, d. h. sie darf nicht weiter in andere Teilmengen unterteilt werden, denn wenn diese existierten, hätten sie keine kausale Bedeutung.
Nehmen wir nun beispielsweise an, dass die Populationsstichprobe , zu der unsere gute Patientin Mary Poppins gehört, eine Kategorie von Probanden im Alter von 20 bis 70 Jahren ist. Wir nehmen auch an, dass wir in dieser Population diejenigen haben, die die Elemente präsentieren, die zu der gehören Datensatz die den oben genannten Labortests entsprechen und precisa in 'The logic of classical language'.
Nehmen wir an, dass wir in einer Stichprobe von 10.000 Probanden von 20 bis 70 eine Inzidenz von 30 Probanden haben, die klinische Anzeichen von und zeigen. Wir haben es vorgezogen, diese Berichte zur Demonstration des probabilistischen Prozesses zu verwenden, da in der Literatur die Daten bzgl Klinische Anzeichen und Symptome für Kiefergelenkserkrankungen weisen unserer Meinung nach eine zu große Variation sowie eine zu hohe Inzidenz auf.[3][4][5][6][7][8]
Ein Beispiel für eine Partition mit vermuteter Wahrscheinlichkeit, bei der eine Kiefergelenksdegeneration (Grad.TMJ) in Verbindung mit Kiefergelenkserkrankungen (TMDs) auftritt, wäre die folgende:
| Wo | |||
| Wo | |||
| Wo | |||
| Wo |
- «A homogeneous partition provides what we are used to calling Differential Diagnosis.»
Klinische Situationen
Diese bedingten Wahrscheinlichkeiten demonstrieren, dass jede der vier Unterklassen der Partition kausal relevant für die Patientendaten in der Bevölkerungsstichprobe ist. Angesichts der oben erwähnten Partition der Referenzklasse haben wir die folgenden klinischen Situationen:
- Mary Poppins Degeneration des Kiefergelenks Kiefergelenkserkrankungen
- Mary Poppins Degeneration des Kiefergelenks keine Kiefergelenkserkrankungen
- Mary Poppins keine Degeneration des Kiefergelenks Kiefergelenkserkrankungen
- Mary Poppins keine Degeneration des Kiefergelenks keine Kiefergelenkserkrankungen
Um zu der obigen endgültigen Diagnose zu gelangen, führten wir eine probabilistisch-kausale Analyse des Gesundheitszustands von Mary Poppins durch, deren Ausgangsdaten waren.
Im Allgemeinen können wir von einem logischen Prozess sprechen, in dem wir die folgenden Elemente untersuchen:
- ein Individuum:
- seinen Anfangsdatensatz
- eine Populationsstichprobe , zu der es gehört,
- eine Basiswahrscheinlichkeit
An dieser Stelle sollten wir zu spezialisierte Argumente einführen, die den Leser vom Thema ablenken würden, die aber eine hohe epistemische Bedeutung haben, für die wir versuchen werden, den am besten beschriebenen logischen Faden des Analysandum/Analysans-Konzepts herauszuziehen. Die probabilistisch-kausale Analyse von ist dann ein Paar der folgenden logischen Formen (Analysandum / Analysans[9]):
- Analysand : ist eine logische Form, die zwei Parameter enthält: Wahrscheinlichkeit , eine Person auszuwählen, die die Symptome und Elemente hat, die zur Menge gehören, und die generische Person , die für diese Symptome anfällig ist.
- Analysator : ist eine logische Form, die drei Parameter enthält: die Partition , die generische Person , die zur Populationsstichprobe gehört, und (Wissensbasis), die einen Satz von Aussagen zur bedingten Wahrscheinlichkeit enthält.
Beispielsweise kann daraus geschlossen werden, dass die definitive Diagnose die folgende ist:
bedeutet das, dass unsere Mary Poppins zu 95% von CMDs betroffen ist, da sie zusätzlich zu den positiven Daten eine Degeneration des Kiefergelenks hat
For example, it can be concluded that the definitive diagnosis is the following:
- this means that our Mary Poppins is 95% affected by TMDs, since she has a degeneration of the Temporomandibular Joint in addition to the positive data
- ↑ Sarkar S, «Nagel on Reduction», in Stud Hist Philos Sci, 2015».
PMID:26386529
DOI:10.1016/j.shpsa.2015.05.006 - ↑ DN model of scientific explanation, also known as Hempel's model, Hempel–Oppenheim model, Popper–Hempel model, or covering law model
- ↑ Pantoja LLQ, De Toledo IP, Pupo YM, Porporatti AL, De Luca Canto G, Zwir LF, Guerra ENS, «Prevalence of degenerative joint disease of the temporomandibular joint: a systematic review», in Clin Oral Investig, 2019».
PMID:30311063
DOI:10.1007/s00784-018-2664-y - ↑ De Toledo IP, Stefani FM, Porporatti AL, Mezzomo LA, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of otologic signs and symptoms in adult patients with temporomandibular disorders: a systematic review and meta-analysis», in Clin Oral Investig, 2017».
PMID:27511214
DOI:10.1007/s00784-016-1926-9 - ↑ Bonotto D, Penteado CA, Namba EL, Cunali PA, Rached RN, Azevedo-Alanis LR, «Prevalence of temporomandibular disorders in rugby players», in Gen Dent».
PMID:31355769 - ↑ da Silva CG, Pachêco-Pereira C, Porporatti AL, Savi MG, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of clinical signs of intra-articular temporomandibular disorders in children and adolescents: A systematic review and meta-analysis», in Am Dent Assoc, 2016». - PMCID:26552334
DOI:10.1016/j.adaj.2015.07.017 - ↑ Gauer RL, Semidey MJ, «Diagnosis and treatment of temporomandibular disorders», in Am Fam Physician, 2015».
PMID:25822556 - ↑ Kohlmann T, «Epidemiology of orofacial pain», in Schmerz, 2002».
PMID:12235497
DOI:10.1007/s004820200000 - ↑ Westmeyer H, «The diagnostic process as a statistical-causal analysis», in APA, 1975».
DOI:10.1007/BF00139821
This is an Open Access resource!