Masticationpedia

Difference between revisions of "Store:QLMit02"

Store Discussion
Line 1: Line 1:
== Introduction ==
== Introduzione ==
I metodi matematici standard furono originariamente sviluppati per servire la fisica classica. L'analisi reale servì come base matematica della meccanica newtoniana (Newton, 1687)<ref>{{cita libro  
I metodi matematici standard furono originariamente sviluppati per servire la fisica classica. L'analisi reale servì come base matematica della meccanica newtoniana (Newton, 1687)<ref>{{cita libro  
  | autore = Newton Isaac
  | autore = Newton Isaac

Revision as of 19:11, 10 November 2022

Introduzione

I metodi matematici standard furono originariamente sviluppati per servire la fisica classica. L'analisi reale servì come base matematica della meccanica newtoniana (Newton, 1687)[1] (e più tardi del formalismo Hamiltoniano); la meccanica statistica classica stimolò l'approccio della teoria della misura alla teoria della probabilità, formalizzata nell'assiomatica di Kolmogorov (Kolmogorov, 1933).[2] Tuttavia, il comportamento dei sistemi biologici differisce essenzialmente dal comportamento dei sistemi meccanici, ad esempio corpi rigidi, molecole di gas o fluidi. Pertanto, sebbene la "matematica classica" svolga ancora il ruolo cruciale nella modellazione biologica, sembra che non possa descrivere completamente la ricca complessità dei biosistemi e le peculiarità del loro comportamento, rispetto ai sistemi meccanici. Sono disponibili nuovi metodi matematici per la modellazione dei biosistemi.(a,b)


In questo articolo, presentiamo le applicazioni del formalismo matematico della meccanica quantistica e la sua metodologia per modellare il comportamento dei biosistemi. (c) Gli ultimi anni sono stati caratterizzati da un'esplosione di interesse per le applicazioni della teoria quantistica al di fuori della fisica, in particolare nella psicologia cognitiva, processo decisionale, elaborazione delle informazioni nel cervello, biologia molecolare, genetica ed epigenetica e teoria dell'evoluzione. Chiamiamo i modelli corrispondenti simil-quantistico. Non sono diretti alla modellazione a micro-livello di processi fisici quantistici reali nei biosistemi, ad esempio nelle cellule o nel cervello (cfr. con applicazioni biologiche della teoria fisica quantistica genuina di Penrose 1989,[3] Umezawa 1993,[4] Hameroff 1994,[5] Vitiello 1995,[6] Vitiello 2001,[7] Arndt et al., 2009,[8] Bernroider e Summhammer 2012,[9] Bernroider 2017[10]). La modellazione quantistica funziona dal punto di vista della teoria quantistica come teoria della misurazione. Questo è il punto di vista originale di Bohr che ha portato all'interpretazione di Copenaghen della meccanica quantistica (vedi Plotnitsky, 2009[11] per una presentazione dettagliata e chiara delle opinioni di Bohr). Una delle principali biospecialità è la considerazione delle auto-misurazioni che i biosistemi effettuano su se stessi. Nella nostra modellizzazione, la capacità di eseguire auto-misurazioni è considerata la caratteristica di base delle funzioni biologiche (vedi Sezione 8.2 e documento Khrennikov et al., 2018[12]).


I modelli quantistici (Khrennikov, 2004b[13]) riflettono le caratteristiche dei processi biologici che corrispondono naturalmente al formalismo quantistico. In tale modellazione, è utile esplorare la teoria dell'informazione quantistica, che può essere applicata non solo al micro-mondo dei sistemi quantistici. In generale, i sistemi che elaborano le informazioni in modo quantistico non devono necessariamente essere sistemi fisici quantistici; in particolare, possono essere biosistemi macroscopici. Sorprendentemente, la stessa teoria matematica può essere applicata a tutte le scale biologiche: dalle proteine, cellule e cervelli all'uomo e agli ecosistemi; possiamo parlare di biologia dell'informazione quantistica (Asano et al., 2015a[14]).


Nella modellazione quantistica, la teoria quantistica è considerata come calcolo per la previsione e la trasformazione delle probabilità. Il calcolo della probabilità quantistica (QP) (Sezione 2) differisce essenzialmente dal calcolo della probabilità classica (CP) basato sull'assiomatica di Kolmogorov (Kolmogorov, 1933[15]). In CP, gli stati dei sistemi casuali sono rappresentati da misure di probabilità e osservabili da variabili casuali; in QP, gli stati dei sistemi casuali sono rappresentati da vettori normalizzati in uno spazio di Hilbert complesso (stati puri) o generalmente da operatori di densità (stati misti).

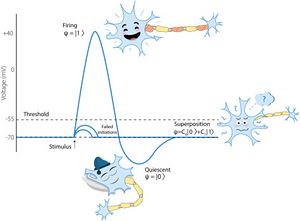
Le sovrapposizioni rappresentate da stati puri sono usate per modellare l'incertezza che non è ancora risolta da una misura.


L'uso delle sovrapposizioni in biologia è illustrato dalla Fig. 1 (vedi Sezione 10 e documento Khrennikov et al., 2018[12] per il modello corrispondente). L'aggiornamento QP risultante da un'osservazione si basa sul postulato di proiezione o trasformazioni più generali degli stati quantistici, nel quadro della teoria degli strumenti quantistici (Davies e Lewis, 1970,[16] Davies, 1976,[17] Ozawa, 1984,[18] Yuen, 1987,[19] Ozawa , 1997,[20] Ozawa, 2004,[21] Okamura e Ozawa, 2016[22]) (Sezione 3).

Figura 1: Illustrazione per la rappresentazione quantistica dell'incertezza generata dal potenziale d'azione del neurone (originariamente pubblicata in Khrennikov et al. 2018)

Sottolineiamo che la modellazione quantistica eleva il ruolo di convenienza e semplicità della rappresentazione quantistica di stati e osservabili. (Ignoriamo pragmaticamente il problema dell'interrelazione di CP e QP.)

In particolare, lo spazio degli stati quantistici ha la struttura lineare e i modelli lineari sono più semplici. La transizione dalla dinamica classica non lineare dei processi elettrochimici nei biosistemi alla dinamica lineare quantistica accelera essenzialmente l'evoluzione dello stato (Sezione 8.4).

Tuttavia, in questo quadro "stato" è lo stato di informazione quantistica di un biosistema utilizzato per l'elaborazione di un'incertezza quantistica speciale (Sezione 8.2).

  1. ↑ Newton Isaac, «Philosophiae naturalis principia mathematica», Benjamin Motte, 1687, London UK». 
  2. ↑ Kolmogorov A.N.Grundbegriffe Der Wahrscheinlichkeitsrechnung. Springer-Verlag, Berlin (1933)
  3. ↑ Penrose R. The Emperor’S New Mind Oxford Univ. Press, New-York (1989)
  4. ↑ Umezawa H. Advanced Field Theory: Micro, Macro and Thermal Concepts AIP, New York (1993)
  5. ↑ Hameroff S. Quantum coherence in microtubules. a neural basis for emergent con- sciousness? J. Cons. Stud., 1 (1994)
  6. ↑ Vitiello G. Dissipation and memory capacity in the quantum brain model Internat. J. Modern Phys. B, 9 (1995), p. 973
  7. ↑ Vitiello G. My Double Unveiled: The Dissipative Quantum Model of Brain, Advances in Consciousness Research, John Benjamins Publishing Company(2001)
  8. ↑ Arndt M., Juffmann T., Vedral V. Quantum physics meets biology HFSP J., 3 (6) (2009), pp. 386-400, 10.2976/1.3244985
  9. ↑ Bernroider G., Summhammer J. Can quantum entanglement between ion transition states effect action potential initiation? Cogn. Comput., 4 (2012), pp. 29-37
  10. ↑ Bernroider G. Neuroecology: Modeling neural systems and environments, from the quantum to the classical level and the question of consciousness J. Adv. Neurosci. Res., 4 (2017), pp. 1-9
  11. ↑ Plotnitsky A. Epistemology and Probability: Bohr, Heisenberg, SchrÖdinger and the Nature of Quantum-Theoretical Thinking Springer, Berlin, Germany; New York, NY, USA (2009
  12. ↑ 12.0 12.1 Khrennikov A., Basieva I., PothosE.M., Yamato I. Quantum Probability in Decision Making from Quantum Information Representation of Neuronal States, Sci. Rep., 8 (2018), Article 16225
  13. ↑ Khrennikov A. On quantum-like probabilistic structure of mental information Open Syst. Inf. Dyn., 11 (3) (2004), pp. 267-275
  14. ↑ Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Quantum information biology: from information interpretation of quantum mechanics to applications in molecular biology and cognitive psychology Found. Phys., 45 (10) (2015), pp. 1362-1378
  15. ↑ Kolmogorov A.N. Grundbegriffe Der Wahrscheinlichkeitsrechnung Springer-Verlag, Berlin (1933)
  16. ↑ Davies E.B., Lewis J.T. An operational approach to quantum probability Comm. Math. Phys., 17 (1970), pp. 239-260
  17. ↑ Davies E.B. Quantum Theory of Open Systems. Academic Press, London (1976)
  18. ↑ Ozawa M. Quantum measuring processes for continuous observables J. Math. Phys., 25 (1984), pp. 79-87
  19. ↑ Yuen, H. P., 1987. Characterization and realization of general quantum measurements. M. Namiki and others (ed.) Proc. 2nd Int. Symp. Foundations of Quantum Mechanics, pp. 360–363.
  20. ↑ Ozawa M. An operational approach to quantum state reduction Ann. Phys., NY, 259 (1997), pp. 121-137
  21. ↑ Ozawa M. Uncertainty relations for noise and disturbance in generalized quantum measurements Ann. Phys., NY, 311 (2004), pp. 350-416
  22. ↑ Okamura K., Ozawa M. Measurement theory in local quantum physics J. Math. Phys., 57 (2016), Article 015209
Retrieved from "https://www.masticationpedia.org/index.php?title=Store:QLMit02&oldid=14017"